第二部　信仰と理性論 星加弘文

Chapter 2   信仰と理性の多対多関係 (31)

（注）

■Section 1

[1] 戸田山和久『知識の哲学』産業図書 2007年 p.24-27

[2] 以下参照

今井晋『自然と恩寵』「教義学講座２」日本基督教団出版局 1982年 p.214

B.ラッセル『西洋哲学史２』「聖トマス・アクィナス」みすず書房 1977年

[3] I.カント『純粋理性批判』「第２版序文」BXXX p.43「それだから私は、信仰を容れる場所を得るために知識を除かねばならなかった。」

[4] 以下参照

Abraham Kuyper, Lectures on Calvinism, Michigah: Eerdmans Publishing Company,1981 p.133「それゆえ、信仰と科学ではなく、二つの科学的体系、言い換えれば二つの科学的な構築物が、互いに己れの信念を持ちながら対立している。」
春名純人『哲学と神学』「キリスト者と非キリスト者の学的思惟における対立の原理」法律文化社 1994年 pp.290-291

■Section 2

[1]『ウェストミンスター信仰告白』新教出版社 1964年　pp.32-35

[2]トマス・アクィナス『神学大全１』「１部第12問題第13項」創文社 1995年 pp.255-256

[3] I.カント「実践理性批判」岩波文庫 1976年 p.51「人間が道徳的法則を遵奉することによって持たなければならない心術は、法則を自発的な傾向やまた命ぜられないでおのずから好んで企てられた努力からではなく、義務に基づいて遵奉するということである。」
B.ラッセル 『私はなぜキリスト教徒でないか』「人類の知的遺産66」講談社 1980年 p.191 「批判の第一はキリスト教神学の知的欺瞞、第二は福音書のイエスにおける道徳的欠陥に向けられている。」

[4] 第一部 信仰論 Chapter 1 - Gigue では、キリスト教信仰とキリスト教倫理の関係付けをほぼ投げ出した状況を書いたが、その後、理解を進めて、両者に「信仰の事実依拠性」と「倫理の非事実依拠性」という関係付けを行った。この状況は、第一部 信仰論 Chapter 2 - Argument 1-3 の中にまとめてある。（2024/4/10）

■Section 3

[1] 岩崎武雄『真理論』東京大学出版会 1976年　p.85

[2] デビッド・ヒューム「人性論」『世界の名著27』大槻春彦編 中央公論社 昭和55年　pp.437-438

[3] W.V.O.クワイン「経験主義の二つのドグマ」『論理的観点から』勁草書房 1996年 p.31

[4] ポール・リクール「隠喩と解釈学の中心問題」『解釈の革新』白水社 2005年 p.89

[5] B.ラッセル『西洋哲学史３』“フランシス・ベイコン” みすず書房 1976年 p.538「現在までのところ、仮説を規則的に発案することを可能にするような方法は、ぜんぜん見出されてはいない」

[6] 野矢茂樹『論理学』東京大学出版会 1996年 p.164

■Easy study 1

[1] G.W.ライプニッツ「哲学の諸原理あるいは単子論 [33] 」『人類の知的遺産38』講談社 1981年 p.314

[2] アリストテレス『形而上学』(上)Γ（第四巻第七章）岩波文庫 1998年

[3] 以下の「背の高い人間」の例は、B.ラッセル『西洋哲学史３』“カント”みすず書房 1976年 p.699 による。

[4] プラトン『パイドン』“想起説による霊魂不滅の証明” 岩波文庫 1998年 pp.61-62

■Easy study 2

[1] トマス・アクィナス『神学大全１』「Ⅰ第一問題第二項主文」 創文社 1995年　p.8

[2] 前件肯定式の全体は(Ａ⊃Ｂ)∧Ａ⊃Ｂ（後出）。なお、結合子の結びつきの優先順の決まりにより (Ａ⊃Ｂ)∧Ａ⊃Ｂは、((Ａ⊃Ｂ)∧Ａ)⊃Ｂ の意味である。

[3] 野矢茂樹『論理学』東京大学出版会 1996年

[4] Ａ∨Ｂの真理表を言葉だけで述べる場合は「Ａ、Ｂが共に偽のとき、またそのときにのみ偽」と述べられる。これは「Ａ、Ｂが共に偽のとき偽」とだけ述べた場合、前節の父親の約束の例でみたように、「～のとき（ならば）」が「Ａ∨Ｂは、Ａ、Ｂが共に偽のとき偽だが、他の場合にも偽でありえる」ことを意味することがあるためである。もちろん「Ａ、Ｂが共に偽のときに偽」ということがＡ∨Ｂの真理表の補足説明として述べられている場合は、真理表を見れば「Ａ、Ｂが共に偽のとき」というのは一通りしかないことが明らかなのでそれでよい。しかし真理表に頼らずに言葉だけでＡ∨Ｂの真理値に言及する場合は、冒頭のように「～のとき、かつそのときに限り」「～ならば、かつその場合にだけ」などと述べる必要がある。

[5] 野矢茂樹『論理学』東京大学出版会 1996年 p.40
大出晃『自然な推論のための論理学』勁草書房 1991年 p.67「前提が真であるのに、結論が偽となることのない推論」
「推論の正しさ」の考え方は、論理式の証明過程で使われるだけでなく、公理系の無矛盾性や健全性についての証明過程としても使われる重要な考え方である。

[6] 前提は正しいが、しかし正しい帰結を導くとは限らないこの種の推論として、

　　「鯨が魚なら鯨は泳ぐ」

　　「鯨は魚ではない」

　　「それゆえ鯨は泳がない」

というのがある。（前掲書 p.42より）

ここでは推論△⊃○の前提△に相当する二つの言明「鯨が魚なら鯨は泳ぐ」「鯨は魚ではない」はいずれも正しい。初めの「鯨が魚なら鯨は泳ぐ」はＰ⊃Ｑとしての前件が間違っているので、⊃の定義によりＰ⊃Ｑ全体は真である。二番目の言明「鯨は魚ではない」は事実に照らして正しい。したがって正しい二つの言明を結合した前提△の言明はやはり正しい。しかしその推論帰結○は間違っている。

したがってこの「鯨の推論」は、前提が正しいとき結論が誤りとなる「不適切な推論」を真理表の行に持つトートロジーではない推論であり、それゆえ「正しい推論」ではない。

 

この「鯨の推論」は、前提1のＰ⊃Ｑの前件Ｐを前提2で否定する「前件否定式」という論理形式であり、その状況は次の真理表から確認できる。ここでＰは「鯨は魚である」、Ｑは「鯨は泳ぐ」である。

 

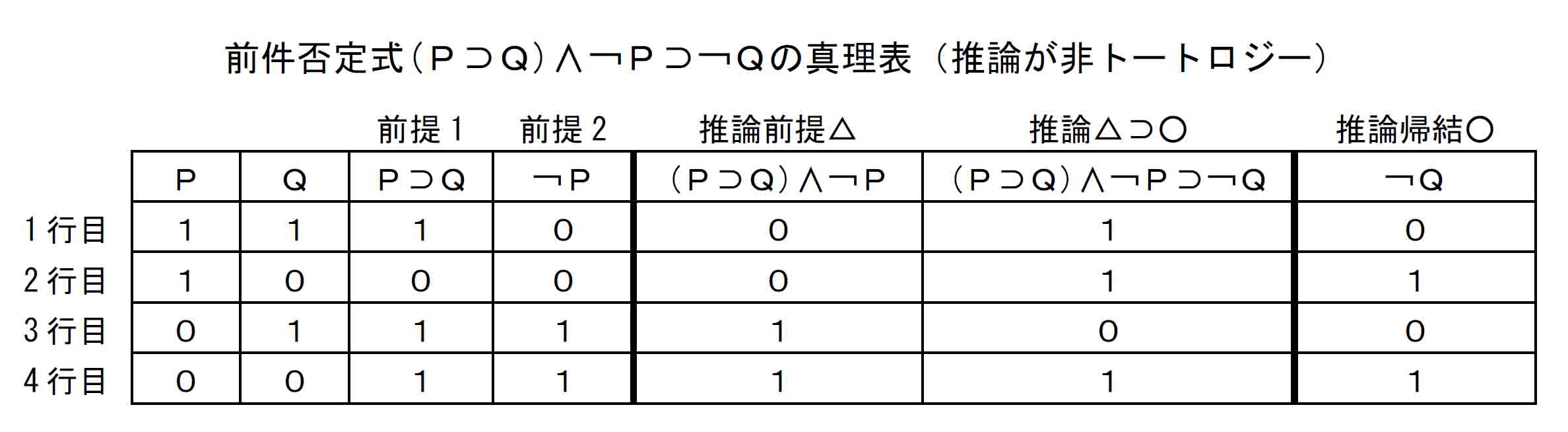
前件否定式(Ｐ⊃Ｑ)∧￢Ｐ⊃￢Ｑの真理表

 

△⊃○の前提△が正しいのは3行目と4行目だが、3行目は推論△⊃○が偽であり、この式がトートロジーではないことを示すものとなっている。

しかし、この非トートロジーである前件否定式は、結論￢Ｑに必ず偽を導くものではない。前提△が偽である1、2行目はここでは問題にしないとして、前提が正しい4行目では￢Ｑは真として帰結している。

つまり、前提が正しい前件否定式はある時は真、またある時は偽の帰結を導くということである。そして、この種の推論の実際において、その具体例が真理表のいずれの行に該当するのかは、△を構成する原子命題Ｐ、Ｑの真偽によって決まる。

「鯨の推論」においては、鯨は、実際、魚ではないが泳ぐので、Ｐは偽、Ｑは真であり、それは真理表の3行目である。このとき△⊃○の値は0で、この行が「不適切な推論」であることを示している。それはこの具体例によって、前件否定式の推論としての「正しくなさ」が示されているということである。

 

鯨を「飛行船」に取り替えてみると、飛行船は魚ではなく泳ぎもしないので、Ｐは偽、Ｑは偽であり、真理表の4行目に該当する。このとき￢Ｑ列は1であり「飛行船は泳がない」という正しい結論が出る。そして前提△および推論△⊃○は1なので、こちらは「適切な推論」である。

ただしこの「適切な推論」というのは真理表の行レベルで言えることであり、真理表レベルでの「正しい推論」というものとは違うことに注意しなければならない。「正しい推論」であるためには、その真理表に「不適切な推論」があってはならず、単に「適切な推論」が存在することがその資格となるのではない。

トートロジーではない真理表では「⊃」の定義から、前提が真で帰結が偽となる「不適切な推論」が必ず含まれるので、トートロジーではない推論は「適切な推論」を含んでいても「正しい推論」にはならない。

したがって、以下の「飛行船の推論」は、前提も結論も正しい「適切な推論」ではあるが、「正しい推論」ではない。つまり論理としては正しくない。言っていることは皆正しいが理屈としては間違っている例である。

　　「飛行船が魚なら飛行船は泳ぐ」

　　「飛行船は魚ではない」

　　「それゆえ飛行船は泳がない」

 

「正しい推論」における「正しさ」とは、命題の内容を捨象した推論の論理形レベルでの正しさをいうのであり、時に正しく（飛行船の推論）、時に間違い（鯨の推論）となるような論理形の推論は「正しい推論」とは言えない、あるいはそう言わないことにする、というのがここにある考え方である。ここで言う「推論の正しさ」とは「推論形式の正しさ」のことであり、これが論理学の祖アリストテレスが見出した論理学の基本的な考え方だったのである。（大出晃『自然な推論のための論理学』p.15）

 

ところで、鯨の推論が一見もっともらしくみえるのは、この前件否定式という「正しくない推論」の真理表の中に「適切な推論」が含まれていることによる。飛行船のような「魚ではなく泳がないもの」を命題に割り当てるとき、その推論は正しい帰結をもたらす。そしておそらく「魚ではなく泳ぐもの」よりは「魚ではなく泳がないもの」の方がはるかに見つけやすいという事情が相まって、その際の「適切な推論」が推論形式までを正しく見させているのである。

 

また、鯨の推論がもっともらしくみえる理由はそれだけではなく、当節冒頭に述べた「ならば」が持つ二義性のためでもある。前件否定式における「ならば」は「条件法」であり、鯨の推論の前提1での「ならば」を条件法と解するとき、鯨の推論は先の「前件否定式の真理表」の通りトートロジーではない推論となる。

ところが前提1の「ならば」を「ならば」がもつもう一つの意味である「同値」に解するなら、この推論は下の通りトートロジーの推論になり、前提△が正しい唯一の行（4行目）において、結論○も正しいことが確認できる。真理表などというものなしに、推論の文章だけを読んで考えようとする場合には、このような二義性を意識することは難しい。

 

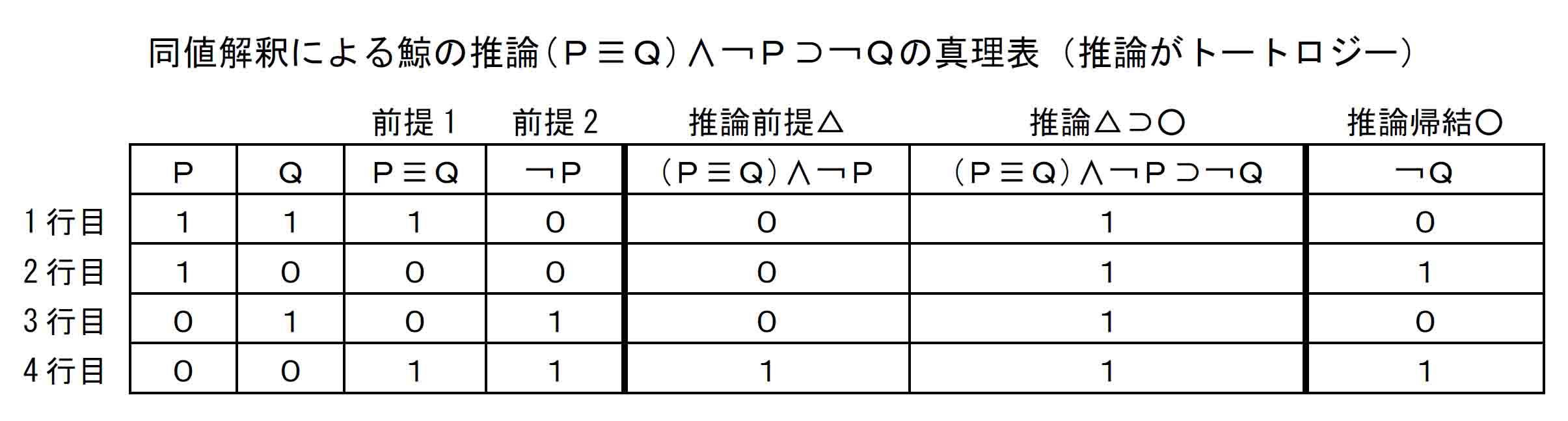
同値解釈による鯨の推論(Ｐ≡Ｑ)∧￢Ｐ⊃￢Ｑの真理表

 

この状況を意味内容から確認してみる。鯨の推論では魚が泳ぐことについては暗黙のうちに前提されているが、魚以外のものが泳ぐかどうかについては言及されていない。そのため前提1の「ならば」は条件法の「⊃」と捉えるのがどちらかと言えば適切な理解であって、この場合は先の「前件否定式」の推論となる。

しかし前提1の「鯨が魚ならば鯨は泳ぐ」を、「明日晴れた場合にだけ動物園に行く」というのと同様に、「魚以外のものは泳がない」を含意したものとして受け取ることも、日常言語の「ならば」の使い方からするとけっして間違いとは言えない。

するとこの場合は、泳ぐのは魚だけなので、Ｐの「鯨は魚である」と、Ｑの「鯨は泳ぐ」は同値関係となる。鯨は、それが魚である場合にだけ泳ぐ生き物であり（1行目に該当）、魚でない場合は泳がない生き物である（4行目に該当）。

そして先の「正しい推論」の定義によれば、トートロジーであり、かつ前提が正しいときに必ず正しい結論を導く推論が「正しい推論」であったから、上の「同値解釈による鯨の推論」は「正しい推論」である。そこでは推論可能な4行のうち前提△が正しいのは4行目だけであり、そこでの結論○は真だからである。

つまり、「ならば」を同値の意味に解釈したときに、この推論が「正しい推論」となるというこのことが、鯨の推論をもっともらしいものに見させているもう一つの理由といえる。条件法と同値の真理値の違いが真理表の3行目にだけ現れることに注目すれば、「正しい推論」と「正しくない推論」についての理解がさらに得られることだろう。

[7] 「トートロジー」と「定理」は混同しやすいが、意味論によって定められた論理的真理の式が、古典論理においては「トートロジー」であり、直観主義論理においては「妥当式」である。「トートロジー」と「妥当式」は意味論の用語であり、「定理」は構文論の用語である。意味論が定める論理的真理の式つまり「トートロジー」あるいは「妥当式」である論理式のすべてを「定理」として導き出せる公理系を「完全」な公理系という。また、公理から導出される「定理」のすべてが意味論の定める論理的真理の式であるときその公理系を「健全」という。

■Easy study 3

[1] 宗教教義が後件肯定式型の論理であることについては「信仰論」Chapter 3-Consideration 参照

[2] 「信仰論」Chapter 3-Mission 参照

■Easy study 4

[1] B.ラッセル『西洋哲学史３』みすず書房 1976年 p.584

[2] 野矢茂樹『論理学』pp.90-91, 102-103 参照

[3] ジョナサン・カラー『文学理論』岩波書店 2003年参照

[4] P.リクール「哲学と宗教言語の特殊性」『解釈の革新』白水社 2005年 p.77

[5] P.リクール「隠喩と解釈学の中心問題」前掲書 p.106

■Easy study 5

[1] 市川秀志『カントールの区間縮小法』株式会社パレード 2007年 pp.118-121

[2] 野矢茂樹『入門！論理学』中央公論新社 2006年 pp.50-54（No.2348重要）

[3] 野矢茂樹『論理学』問題77(1)に関連して巻末（p.216）に二重否定除去則を使った排中律の証明がある。この証明では二重否定除去則が使えないと排中律が証明されないので、排中律が二重否定除去則に依存しているといえるが、ここでは以下の証明を示す。
----------------
排中律Ａ∨￢Ａは形式上は両立的選言だが、実質的には「Ａでないならば￢Ａ」あるいは「￢ＡでないならばＡ」をいう排反的選言Ａ▽￢Ａである。なぜならこれが両立的選言であればＡ∧￢Ａを含むことになり、矛盾律￢（Ａ∧￢Ａ）に抵触するからである。
いま直観主義論理において￢￢Ａ⊃Ａが言えないことが確認できたとする。（この確認はSection 5-2の最後で行われる。）
￢￢Ａとは「￢Ａではない」ことなので、「￢￢Ａ⊃Ａ」が言えないとは、「￢ＡでないならばＡ」が言えないということであり、これは排他的選言Ａ▽￢Ａが言えないということと同じである。
したがって￢￢Ａ⊃Ａが認められないとき、それと一蓮托生にＡ∨￢Ａも認められない。
----------------
なお、大出晃『自然な推論のための論理学』p.52（例 4.）に、排中律から二重否定除去則が導かれることが示されている。

■Hard study 5-2-3

[4] 以下の証明で「～のとき」「～ならば」という語が「直観主義論理の意味論」規定Ⅱ(1)～(5)の同値式から派生して使われている場合は、当然ながら「条件法」ではなく「同値」を意味している（条件法と同値については、Easy Study 2-2 参照）。「ＡならばＢ」「ＡのときＢ」が条件法として述べられた場合はＡの偽であることはＢの真偽を決定しないが、同値として述べられた場合はＡの偽であることがＢの偽であることを決定する。
したがって以下の証明での「～のとき」「～ならば」は、「～のとき、かつそのときに限り」「～ならば、かつその場合にだけ」という同値の意味である。

■Hard study 5-3-2

[5] ここで「二重否定除去則が矛盾律を含む」とは次の意味。￢￢Ａは「￢Ａではない」こと、つまり「￢Ａを仮定すると矛盾Ｄ∧￢Ｄが出る」ということである。そこでLPの二重否定除去則は「￢Ａを仮定すると矛盾Ｄ∧￢Ｄが出るときはＡを導出してよい」ということである。これに対してLIPの否定除去則は「矛盾Ｄ∧￢Ｄが出るときはＡを導出してよい」というものでこれは矛盾律の言い替えである。つまりLIPの否定除去則は、LPの二重否定除去則の「￢Ａを仮定すると」を取り除いて矛盾律の部分を残したものといえる。
なお野矢茂樹『論理学』ではLIPはLPの否定除去則を「弱い形」に代えたものと述べられている。戸田山和久『論理学をつくる』名古屋大学出版会 2002年 p.293によると、論理学での規則の「弱い」「強い」というのは、強い規則は弱い規則のすべてをできるが、弱い規則は強い規則のすべてを実現できないということである。
確かに、LIPの否定除去則は、論理に矛盾が出た時は何を述べてもよいということにして論理が破綻したことを宣言するものであるのに対し、LPの二重否定除去則は矛盾が出た時にもし￢Ａが仮定されていたのならＡを導出してよいという、仮定と関連のある反対命題の導出を述べるもので、これはLIPの規則ではできないことである。￢Ａだとすることが間違いであるとき、LPではＡが結論となるが、LIPでは結論は必ずしもＡとはならない。LIPではこのときＡもまた誤り（不証明）でありえるからである。

■Hard study 5-4-2

[6] 野矢茂樹『論理学』では「ω(ｘ)を『ｘは自分自身に述語づけられないような述語である』という命題関数であるとする」となっているが（p.131）、分かりにくい表現なので、当論考ではω(ｘ)のωを「主語ｘをそのまま述語にして使うことができない性質の述語」と言いかえている。

[7] 野矢茂樹『入門！論理学』p.40

[8] 野矢茂樹『論理学』p.128 に、命題関数と集合の同等性として次の規定がある。
----------------
　述語「∈SF」を次のように規定する。
　(x∈SF)≡Fx
----------------
命題関数 Fx「xは、Fである」とは、x∈SF「xは、Fである集合Sの要素である」と同等ということである。述語「∈SF」だけを読めば「Fである集合Sの要素である」ということで、これが Fx の F に相当する。
命題関数 Fx の F を「犬である」とすると、集合側ではそれは「犬である集合Sの要素である」、つまり「犬の集合の要素である」ということになる。
そこで、命題 [『犬である』は「犬である」] の述語「犬である」を集合の読みにすると、[『犬である』は「犬の集合の要素である」]となる。
このとき主語『犬である』が何であるかははっきりしないが、犬の集合の要素、例えば “ポチ” や “チロ” ではないことは明らかなこととしてよいだろう。
ところで、述語だけの文は命題の不完全な形であるから命題関数である。「犬である」と述べることは「xは犬である」と述べたことに等しい。
それゆえ [『犬である』は「犬である」] という文において、述語「犬である」は主語『犬である』を冠しているので命題文の通常の述語だが、主語とされた『犬である』の方は、冠する主語を持たない述部だけの語であるから命題関数と解さざるを得ない。
したがってこの文の主語は “命題関数” だといえる。
あるいはそれは “この文の述語相当語” と言うこともできるし、“4文字”、“文字列”、“日本語” などとも言える。しかし少なくともそれは犬ではない。同書においてもこの扱いをしているということである。
冒頭に定義された「命題関数と集合の同等性」を適用すると、命題関数を主語にした文とは、集合を主語にした文ということである。
この場合、[『犬である』は「犬である」] は、集合を対象に叙述を行う「二階の論理」ということになり、これがラッセルパラドクスの本質であることについては同書の解説により理解される。
また、すべての命題の述部は、そこだけをみれば命題関数であり、すなわち集合であるから、F(F)やG(G)、ω(ω)などの命題関数は「集合の集合」を表わしている。「集合の集合」を考えたときにパラドクスが起こりえることについては前節、当節にみる通りである。

[8.1] D.ジュリア『ラルース哲学事典』p.495 "論理実証主義"「意味論（言語記号とそれが関わる外的対象との関係の学）」

[8.2] この点を考えると、タルスキの「真理の余剰説」は古典論理内では妥当だが、直観主義論理を視野に入れた場合には「～は真である」という述語は余剰ではなく、古典論理と直観主義論理の真理観を区別する述語として働いているといえる。

■Hard study 5-4-3

[9] 野矢茂樹『論理学』p.38

■Hard study 5-4-5

[10] 加藤浩・土屋俊『記号論理学』放送大学教育振興会 2014 p.87

■Hard study 5-5-2

[11] 矢田部俊介「カリー・ハワード対応と直観主義論理意味論入門」2018 p.7 https://www.academia.edu/35826510/%E3%82%AB%E3%83%AA%E3%83%BC_%E3%83%8F%E3%83%AF%E3%83%BC%E3%83%89%E5%AF%BE%E5%BF%9C%E3%81%A8%E7%9B%B4%E8%A6%B3%E4%B8%BB%E7%BE%A9%E8%AB%96%E7%90%86%E3%81%AE%E6%84%8F%E5%91%B3%E8%AB%96%E5%85%A5%E9%96%80

[12] 大出晃『自然な推論のための論理学』p.75

■Hard study 5-5-3

[13] 【直積】例：テーブルＡが2列3行のデータ、Ｂが3列5行のデータからなるとき、2つのテーブルを横に結合して5列15行のテーブルを作る操作。当節で使用するMicrosoft Access®では結合線を設定しないクエリによって行う。
  【内部結合】直積を行った後、Ａ、Ｂの共通列の値が同じであるものを抽出する操作。Accessでは矢印のない結合線を設定して行う。共通列の値がそれぞれ一意であるテーブルでは、ＡテーブルとＢテーブル間の共通列の項目値の一致と、直積テーブルでの共通列の項目値の一致には違いがないので、内部結合について「２つのテーブルに共通しているデータを取り出す」という一般に普及している理解でよい。しかし一対多や多対多の関係にあるテーブルでは、内部結合が「直積を経由した操作」であることを理解していないと結合結果を理解できないか、あるいは結合の結果と結合の意図が一致しないということが起こる。
  【外部結合】内部結合を行った後、内部結合から漏れたデータをＡ、Ｂいずれかの側から採用する操作。Accessでは矢印付の結合線を設定する。共通列の値が一意であるテーブルでは、外部結合を「２つのテーブルのうちいずれかを主テーブルとみなし、他方のテーブルから主テーブルのデータと合致するデータを主テーブル側に引用する」というMicrosoft Excel®のVlookup関数等と同じ操作として理解してよいが、一対多、多対多関係のテーブルの外部結合では「外部結合の動作前に内部結合が直積データにおける項目値の一致において働いている」という理解が必要。つまり外部結合の動作も直積が基礎になっている。

[14] 試みに、この理解に基づいて認識史01と認識史00の⊮記号を別にして、それらの演算規則をいくらか変更した証明表を作成してみたが、ド・モルガン律(2)aの結果はⅠ型と同じである。

[15] 注[14]の結果から、認識史01と認識史00の不証明記号を別のものにしても、それによる証明表での効果がないことが明らかであり、また認識史01は、それが認識史00と分離していることによってその機能を果たしているので認識史01の不証明記号を新たに作る必要はなく、逆に認識史00で使われる記号と重なっていても支障はない。不証明記号を無闇に増やさないためにも、認識史01での直観主義論理的「未証明」と 認識史00での三値論理的「不明」は同じ記号とするのがよいと考える。

[16] ここでは、前件と後件の同じ認識史で├だけの行が├だけの行と、├/だけの行が├/だけの行と対応しているため、├を含む行と、すべてが├/である行を一度の外部結合で操作できるため、認識史行を分ける作業を省略している。No.4 (Ａ⊃Ｂ)⊃(￢Ａ∨Ｂ)では├と├/を分けた操作が必要になる。

■Hard study 5-5-4

[17] 「宇宙とブラックホールのQ&A」「直観主義命題論理で成り立たない論理式とその証明3」2022-09-02　https://ameblo.jp/karaokegurui/entry-12762162236.html　karaokegurui

[18] G.H.フォン・ヴリグト『論理分析哲学』講談社学術文庫 2001年 p.81付近

[19] 「計算機科学関連の数学の参考資料（１）」11th Apr. 2023　https://www.cs-study.com/koga/cmath/cmath01.html#heyting　Akihiko Koga

[20] 古典論理のｘ⊃ｙは￢ｘ∨ｙと同値。この「ｘでないかまたはｙである」という言明は、「ｘでありかつｙではない、というのではない」と言い替えられるので、これを式にすると￢(ｘ∧￢ｙ)であり、これによって⊃が￢と∧から定義されていることになる。そしてこの式を演算化すると1－(ｘ・(1－ｙ))＝1－(ｘ－ｘ・ｙ)＝1－ｘ＋ｘ・ｙとなり、先に見た⊃の演算式となる。

[21] 「計算機科学関連の数学の参考資料（１）」11th Apr. 2023　https://www.cs-study.com/koga/cmath/cmath01.html#heyting　Akihiko Koga

[22] 青山広・愛知非古典論理研究会『論理体系と代数モデル』八千代出版 2007　p.117（命題5.7）
以下の説明では、同書での記法を簡略化し、適宜、当稿に記号類を合わせ、また、見やすさの配慮から式の左辺右辺の入れ替え、それに伴なう不等号の向きの逆転等を行っている。
ａはハイティング代数Ｈの任意の元、ｂはＨの任意の部分集合。
　 ａ∧Vｂ＝V(ａ∧ｂ) を証明するために、
(1) ａ∧Vｂ≧V(ａ∧ｂ)
(2) ａ∧Vｂ≦V(ａ∧ｂ) を証明する。
(1)の証明 まず、ａ∧Vｂ≧ａ∧ｂ。これは右辺「ａとｂ（ｂの任意の元）の小さい方（下限）」よりも、左辺「ａと『ｂの上限』との小さい方（下限）」の方が大きいことは明らかであるため。この関係は右辺のａ、ｂがどんな値をとったとしても成り立つので（右辺のａが大きくなれば左辺のａも大きくなる）、たとえ「ａとｂの下限」の最大のものをとったとしても、それは左辺より小さい。
すなわち、ａ∧Vｂ≧V(ａ∧ｂ)――(1) 証明終わり
(2)の証明 ハイティング代数の中ではハイティング代数の定義式 (ａ∧ｘ)≦ｂ ←→ ｘ≦ａ→ｂ が成り立つので、この変換を利用して以下の式を変形していく。
まず、ａ∧ｂ≦V(ａ∧ｂ)。ａとｂの下限は、当然、「ａとｂの下限」の上限より小さい。
これを定義式の→方向の変換に当てはめると、ｂ≦ａ→V(ａ∧ｂ)
これはｂがどんな値であっても成り立つはずだから、Vｂ≦ａ→V(ａ∧ｂ)
定義式の←方向の変換を適用して、ａ∧Vｂ≦V(ａ∧ｂ)――(2) 証明終わり
(1)、(2)より、ａ∧Vｂ＝V(ａ∧ｂ)

[23]『論理体系と代数モデル』p.110（命題5.1）（以下、ａ、ｂはＨの元）
定義①　(ａ∧ｘ)≦ｂ ←→ ｘ≦ｃ
定義②　Max{ｘ∈Ｈ｜ａ∧ｘ≦ｂ}が存在し、これをａ→ｂとする
定義②と定義①の同等性の証明は、(1) 定義②から①を導き、(2) 定義①から②を導くことによって行う。
(1) 定義②から①の導出
定義②から①の導出は、定義②と定義①左辺を前提して定義①の右辺を導き、さらに、定義②と定義①右辺を前提して定義①の左辺を導くことによって行う。
■定義②と定義①左辺の仮定による定義①右辺の導出は以下。
定義①左辺 (ａ∧ｘ)≦ｂ を仮定すると、定義② ａ→ｂ＝Max{ｘ∈Ｈ｜ａ∧ｘ≦ｂ} より、①左辺の関係を満たすｘの最大のものがａ→ｂにほかならないので ｘ≦ａ→ｂ。定義①右辺が導かれた。
■定義②と定義①右辺の仮定による定義①左辺の導出は以下。
定義①右辺 ｘ≦ａ→ｂ を仮定すると、同じく定義②から、ａ∧ｘ≦ａ∧(ａ→ｂ) すなわち、ａと「ａ→ｂの候補値ｘ」との下限は、ａと「候補値ｘの最大であるａ→ｂ」との下限よりも小さい。これを(A)とする。
ここで、ａ→ｂはｘの最大値であるとはいえ、ｘの範囲内にあるものなので、定義②の式が適用できる。すなわち ａ∧(ａ→ｂ)≦ｂ。これを(B)とする。(A)、(B)より、ａ∧ｘ≦ｂ。定義①左辺が導かれた。
(2) 定義①から②の導出
定義① (ａ∧ｘ)≦ｂ ←→ ｘ≦ａ→ｂ を前提し、左辺のｘに任意にａ→ｂを代入すると、ａ∧(ａ→ｂ)≦ｂ となる。これはａ→ｂを、(ａ∧ｘ)≦ｂを満たすような集合の元ｘの一つとするということなので、定義②の Max{ｘ∈Ｈ｜ａ∧ｘ≦ｂ} とは無関係に、ａ→ｂ∈{ｘ∈Ｈ｜ａ∧ｘ≦ｂ} が得られる。
ところで、ａ∧ｘ≦ｂ を満たすｘは、定義①により、ｘ≦ａ→ｂ すなわちａ→ｂより小さいので、その中には最大値となるようなｘが存在している。
それを式に表すと Max{ｘ∈Ｈ｜ａ∧ｘ≦ｂ} であり、これはａ→ｂの定義②にほかならない。

 

　『論理体系と代数モデル』p.117（命題5.9）
定義②　Max{ｘ∈Ｈ｜ａ∧ｘ≦ｂ}が存在し、これをａ→ｂとする
定義③　ａ∧Vｂ＝V(ａ∧ｂ) が成り立つ
定義②と定義③の同等性の証明は、(1) 定義②から③を導き、(2) 定義③から②を導くことによって行う。
(1) 定義②から③の導出
注[23]命題5.1で、定義①と定義②の同等性が証明されているので、定義①から定義③の分配律が成り立つことを導いた注[22]命題5.7の証明をもって、定義②から定義③の導出とみなすことができる。
(2) 定義③から②の導出
注[23]命題5.1で、定義①と定義②の同等性が証明されているので、定義③から
　定義① (ａ∧ｘ)≦ｂ ←→ ｘ≦ａ→ｂ が導かれることを示せばよい。（そのためには→、←の両方向の証明をそれぞれ示す。）
　(ａ∧ｘ)≦ｂ → ｘ≦ａ→ｂ は、定義②から明らか。定義②は (ａ∧ｘ)≦ｂを満たすｘの最大のものがａ→ｂだと言っているので、当然、ｘ≦ａ→ｂ。したがって、(ａ∧ｘ)≦ｂ → ｘ≦ａ→ｂ。
　(ａ∧ｘ)≦ｂ ← ｘ≦ａ→ｂ は次のように示すことができる。
　ｘ≦ａ→ｂ であるとき、両辺でそれぞれａとの下限をとっても≦の関係は変わらない。すなわち、
　ａ∧ｘ≦ａ∧(ａ→ｂ)。
　またａ→ｂは、ｙを分配律を満たす束Ｌの元とすると max{ｙ∈Ｌ｜ａ∧ｙ≦ｂ}のことなので、
　ａ∧(ａ→ｂ)＝ａ∧V{ｙ∈Ｌ｜ａ∧ｙ≦ｂ}。定義③の分配律によって、
　ａ∧V{ｙ∈Ｌ｜ａ∧ｙ≦ｂ}＝V{ａ∧ｙ∈Ｌ｜ａ∧ｙ≦ｂ}
　ここで、ａ∧ｙ≦ｂであるので、ａ∧ｙを元とする集合Ｌの最大値もまたｂより小さいことは明らか。
　したがって、V{ａ∧ｙ∈Ｌ｜ａ∧ｙ≦ｂ}≦ｂ
　したがって、ｘ≦ａ→ｂ であるとき (ａ∧ｘ)≦ｂ。

[24] 岩村聯『束論』共立出版株式会社 2009年 pp.57-58

[25] 「宇宙とブラックホールのQ&A」「直観主義命題論理で成り立たない論理式とその証明2」2022-08-31 https://ameblo.jp/karaokegurui/entry-12761789579.html　karaokegurui

[26] 『論理体系と代数モデル』p.34

[27] 「ソフトコンピューティング 講義資料（II）」「直観主義論理」平成12年5月17日 https://sagaweb.csse.muroran-it.ac.jp/htdocs_fuzzy/fuzzy2/node17.html　佐賀 聡人

■Easy study 6

[1] 本体論的証明については「信仰論」Chapter 2 - Argument 3 注[2]参照

[2]「今、私は一部分しか知りませんが、その時には、私が完全に知られているのと同じように、私も完全に知ることになります。」第一コリント13.12b

[3] R.ブルトマン『イエス』未来社 1989年 p.12

[4] 野矢茂樹『論理学』p.245「おかしくないことが証明できないとは、おかしいことが証明できたとしても矛盾はないということ」

[5] ブラウアーの弟子A.ハイティングが直観主義論理を公理化したのは1930年で、以後、この考え方に対する理解が広まった。

■Section 4

[1] M.J.ボーグ『イエス・ルネサンス』教文館 1997年 p.363

[2] A.E.マクグラス『歴史のイエスと信仰のキリスト』キリスト新聞社 2011年 p.246「（ブルトマン、パウル・ティリッヒ）キリストへの信仰は歴史的研究の暫定的な結果に基づくことはできない」
ツァールント 前掲書 p.31「レッシングが批判したのは…一般に真理を歴史的な手段で根拠づけ、歴史的な方法で伝達しようとしたことに対してであった。」
K.バルト『教会教義学』第４巻和解論の一 新教出版社 1972年 p.243「間接的報知がわれわれの信仰の基礎となりえるか」
キルケゴール『哲学的断片への結びとしての非学問的あとがき』「キルケゴール著作集7」白水社 1971年 p.174「聖書記事そのものの信憑性が承認されているとしても、そこからなにか決定的な真理が得られるわけではない、とレッシングは主張する。」
山田耕太『聖書学の黎明期のイエス研究』「イエス研究史」日本基督教団出版局 1998年 p.86「歴史の偶然的な真理は、理性の必然的な真理の証明には決して成り得ない」

[3] 稲垣久和『自然法と近代認識論』「基督神学」東京基督神学校 1984年 p.70 稲垣がN.R.ハンソンの「観察における理論負荷性」を「カント認識論の亜流」としているのはその一例。

[4] J.I.パッカー『啓示についての現代の諸見解』「聖書論論集」聖書図書刊行会 1974年 p.127

[5] A.ショーペンハウアー『カント哲学の批判』「意志と表象としての世界 正編Ⅲ」白水社 1975年 p.15「カント最大の功績は現象の物自体からの区別ということである」
黒崎政男『カント「純粋理性批判」入門』講談社選書メチエ 2004年 p.30「そのうちでもっとも重要な前提が、〈物自体〉と〈現象〉との峻別、という発想である。私たちの認識が関わるのは、〈物自体〉ではなく、私たちの感性と悟性とが成立させる〈現象〉であり、まさにそれゆえに、現象の認識は、客観的妥当性を主張しえるものとなるのである。」 p.133「〈物自体〉と〈現象〉との峻別というアイディアこそ、『純粋理性批判』を成立させるもっとも深い考え方なのである。」
岩崎武雄『カント』勁草書房 1981年 p.135「カントがその認識論的主観主義の思想によって成しとげた最大のことは、われわれの認識は決して物自体を把握し得るものではなく、ただ現象を把握し得るにすぎないということであろう。」

[6] カント『純粋理性批判 上』岩波文庫版 1978年 BXXVII, B67, B69

[7] ショーペンハウアー 前掲書 p.56 G.E.シュルツェ（1761-1833）による指摘であることが記されている。

[8] E.アディッケス『カントと物自体』法政大学出版局 1988年 参照

[9] カント 前掲書 A101, BXXVI, B61, 206, 235, 336, 335, 522, 536 566、他に『プロレゴメナ』岩波文庫 1977年 第三二節 p.134等