| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (24)
Hard study 5-5-2 プレ線型性のためのⅠα型証明表
前節ではクリプキ意味論から作成した証明表が、直観主義論理で非定理となる論理式の一部を正しく表現しないことを見た。
クリプキ意味論は直観主義論理に対して健全かつ完全であるということである。
「健全かつ完全である」というのは、クリプキ意味論が導く妥当式(意味論によって論理的真理として定められる式)と、直観主義論理構文論の公理系LIP(野矢茂樹『論理学』p.167等)が導く定理が一致するということである。いずれかが妥当式あるいは定理として導出する式を、他方が非定理あるいは非妥当式として導出することはなく、その逆もない。
しかし前節に見た限り、Ⅰ型証明表は、直観主義論理において非定理であるド・モルガン律の一つ
¬(A∧B)⊃(¬A∨¬B)
と、プレ線型性と呼ばれる
(A⊃B)∨(B⊃A)
を妥当式として表現してしまう。ここではプレ線型性式について検討してみる。
前々節にみた認識史分析は、分析対象の式の構造が単純なものであれば、その式が妥当/非妥当であるということ以上の情報を与えてくれる場合がある。
ある論理式を不証明と仮定して分析を進めた先に矛盾が起きない枝先があるとき、その枝がたどってきた経路は元の式を不証明と仮定しても問題がなかったことを示すものであり、すなわち元の式を不証明と仮定することが正しかったことを示す経路ということができる。それは、その式が妥当式ではないことを示す認識史モデル(原子命題の具体例)を案内するものになっているのである。
例えば、Hard study 5-2-4でみた非定理¬¬P⊃Pを認識史分析すると以下となる。
まず¬¬P⊃Pを不証明であると仮定する。
[1] -(¬¬P⊃P)
この式の一番「外」の論理記号(一番最後に機能する論理記号)である⊃を除去則にかけると、-⊃の将来分析により、
[2] +¬¬P、-P
となる。ここで-Pは原子命題であるので分析対象にならない。もう一方の式の+¬を除去すると、+¬の現状分析により、
[3] +¬¬P、-¬P、-P
となる。新たに出た-¬を除去すると、-¬の将来分析により、
[4] +¬¬P、+P
に行きつく。
+¬が残っているが[2]で分析済みのため、[3]以下と同じ事態を生じさせるだけなのでここで終了。最終枝先[4]には矛盾がないので、[1]で不証明を仮定した-(¬¬P⊃P)は正しい式であったことが判明したということである。したがって¬¬P⊃Pは妥当式ではない。
この[1]~[4]の経路が、¬¬P⊃Pが妥当式ではないことを立証する認識史モデルとなっていることを見てみよう。
[2]で+¬¬Pかつ-Pとなっているので、この状況が成立している認識史を、¬¬PとPを含む「直観主義論理の¬¬Pの証明表」で探すと(認識史途上なのでα期で探す)、α⊩¬¬P、α⊮Pとなっている認識史01があることが分かる。
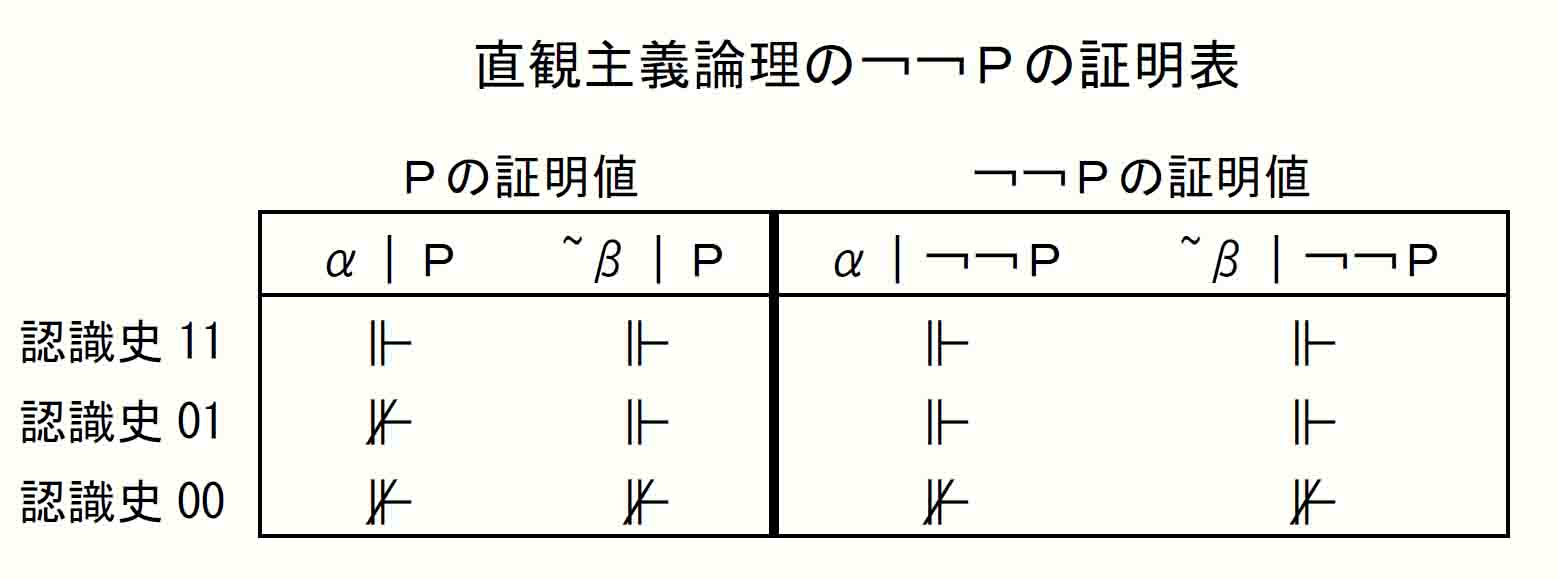
[3]では-¬Pかつ-Pとなっているので、この状況が成立している認識史を、¬PとPを含む「直観主義論理の¬Pの証明表」で探すと、α⊮¬P、α⊮Pとなっている認識史01がある。
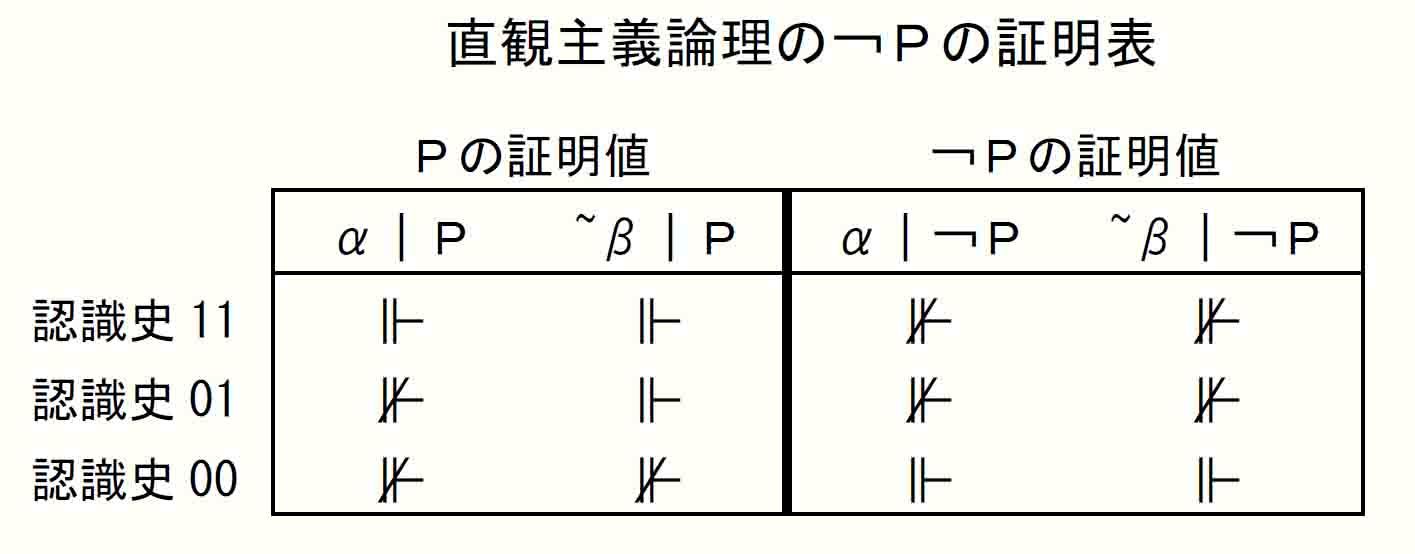
同様に、[4]の+¬¬Pかつ+Pの状況を、先の「直観主義論理の¬¬Pの証明表」で探すと(こちらは最終期なので~β期で探す)、と、認識史11~βと認識史01~βが該当しており、認識史01が[3]の経路の続きであることを確認できる。
これを逆にして、Pを認識史01で[4][3][2]とたどると、[1]の-(¬¬P⊃P)という不証明式にたどり着くということである。その上で「直観主義論理の¬¬P⊃Pの証明表」を見ると、やはりその認識史01で⊮が起きていることが確認されるのである。
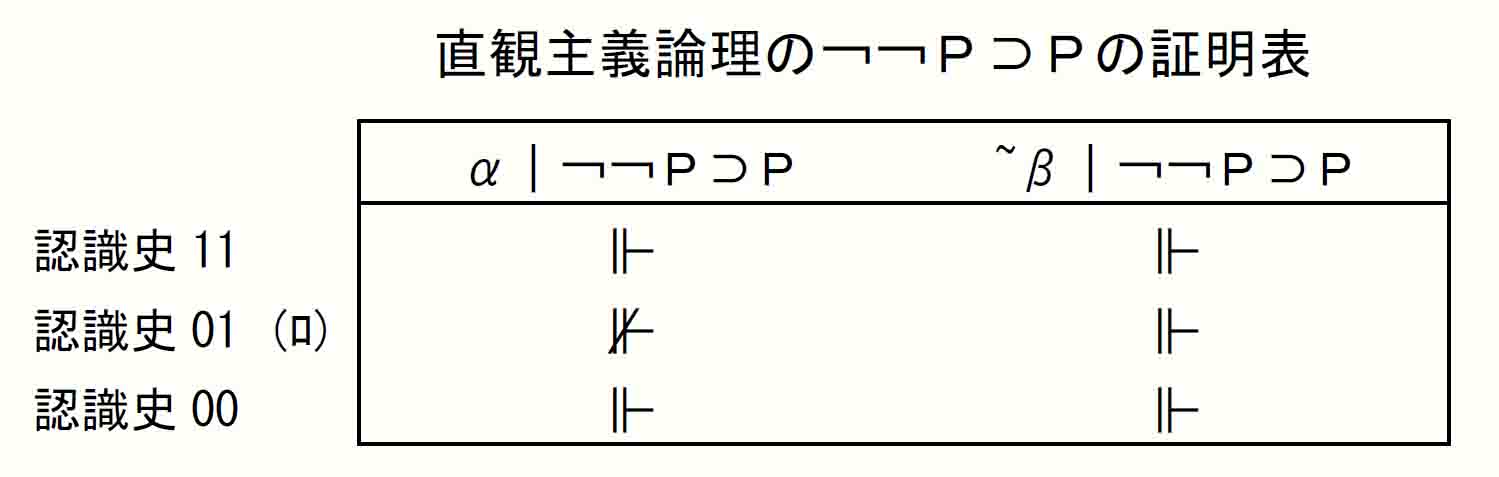
すなわち認識史分析は、ただ式の妥当/非妥当を示すというだけではなく、その式に非妥当性をもたらしている特定の認識史を教えてくれる場合があるということである。
そこで、プレ線型性式(A⊃B)∨(B⊃A)の認識史分析を行うと以下のようになる。
(A⊃B)∨(B⊃A)が不証明であると仮定する。
[1] -((A⊃B)∨(B⊃A))
-∨の現状分析。
[2] -((A⊃B)∨(B⊃A))、-(A⊃B)、-(B⊃A)
-⊃の将来分析。-⊃が複数あるため将来分析は枝分かれする。また将来分析なので-式は受け継がれない。
[3]a -(A⊃B)の将来分析により +A、-B
[3]b -(B⊃A)の将来分析により +B、-A
論理記号がすべて取り除かれたので認識史分析は終了。2個の最終枝先はいずれも矛盾のない式の組み合わせで、元式(A⊃B)∨(B⊃A)が妥当式ではないことが示されている。
認識史分析では、-∧、+∨、+⊃の現状分析で枝分かれが起こるが、このときの枝分かれは「または」の意味合いを持つ。(前々節「+∨の現状分析」参照)
一方、[3]aと[3]bの将来分析での枝分かれは、その前段に-⊃が複数存在したことによる枝分かれであり、こちらは「かつ」の意味合いを持った枝分かれである。これは以下の考察による。
-式の将来分析で複数の枝を発生させることには二つの理由があると考えられる。
一つは、将来分析では他の-式を受け継がないという規則があることによるもので、例えば[2]の-(A⊃B)を将来分析すると、分析済の-((A⊃B)∨(B⊃A))だけでなく未分析の-(B⊃A)も捨てなければならないことになる。-(B⊃A)を将来分析するためには認識史分析を別立てで行わなければならない。
これを避けるため、-⊃や-¬が複数ある場合は、その数だけの将来分析をいっぺんに行う手法を取り、それが枝分かれとして表現されているということである。
もう一つは、認識史分析は論理記号の除去則による式変換なので、その逆の手順の導入則を実行することで元の式に遡ることができるものになっているということのためである。
-(A⊃B)、-(B⊃A)の両方を含む知識状態から次の段階へと式変換を行った場合、そこから元の-(A⊃B)、-(B⊃A)の知識状態に戻ることができるためには、[3]a、[3]bの両方が必要となる。そのため[3]a、[3]bは同時的に書き出されなくてはならない。
これに対して、やはり同時的に書き出す現状分析の枝分かれでは、いずれも枝の片方だけから前段階に遡ることができる。同じ枝分かれでもその性質は違っているのである。
そうであるなら、複数の将来分析は枝分かれさせずに一つの枝に記述してしまえばよいということになりそうだが、そうすると、別々に扱われるべきである複数の式を一つにまとめてしまうこととなって方法として誤ったものになる。例えば[3]a、[3]bを一つの枝先に記述すると知識状態に矛盾が現れてプレ線型性を妥当式としてしまう。
このようなことにならないためには、複数の将来分析は、同時かつ別々に書く必要があり、それが枝分けによる記述ということなのである。
しかしこの結果、将来分析と現状分析の枝分かれは、意味に違いがあるにもかかわらず見かけは同じという事態が生じているということである。したがって『論理学』p.180に示されている枝分かれ図と、p.181のそれとでは枝分かれの働きが違っているのである。
現状分析の枝は片方だけあれば前段階に遡ることができるので、二つの枝同士は「または」の関係にある。一方、将来分析が複数あることによる枝分かれはその両方がないと元に戻れないのでそれらは「かつ」関係にあるという理解となる。そして、複数の将来分析による枝分かれが「かつ」関係にあるというこの理解が、プレ線型性の非妥当性をⅠ型証明表で捉えることを可能にさせるのである。
[3]a(+Aかつ-B)と[3]b(+Bかつ-A)を、前節のⅠ型証明表に当てはめてみる。いずれも論理記号がない知識状態なので、適用するのは「Ⅰ型2命題認識史表」である。
[3]aと[3]bは、これらがどういう由来を持つものであれ相互に矛盾する証明値なので、[3]aと[3]bが完全な意味での「かつ」状態として存在することはない。すなわち一つの認識史の特定の期にこれらの事態が共在することはない。「任意の期の知識状態で矛盾は存在しない」ことが直観主義論理意味論規則に含まれている。
[3]aと[3]bの知識状態が-((A⊃B)∨(B⊃A))の最終状況であることを勘案すると、これを~β期に探すことが適切である。
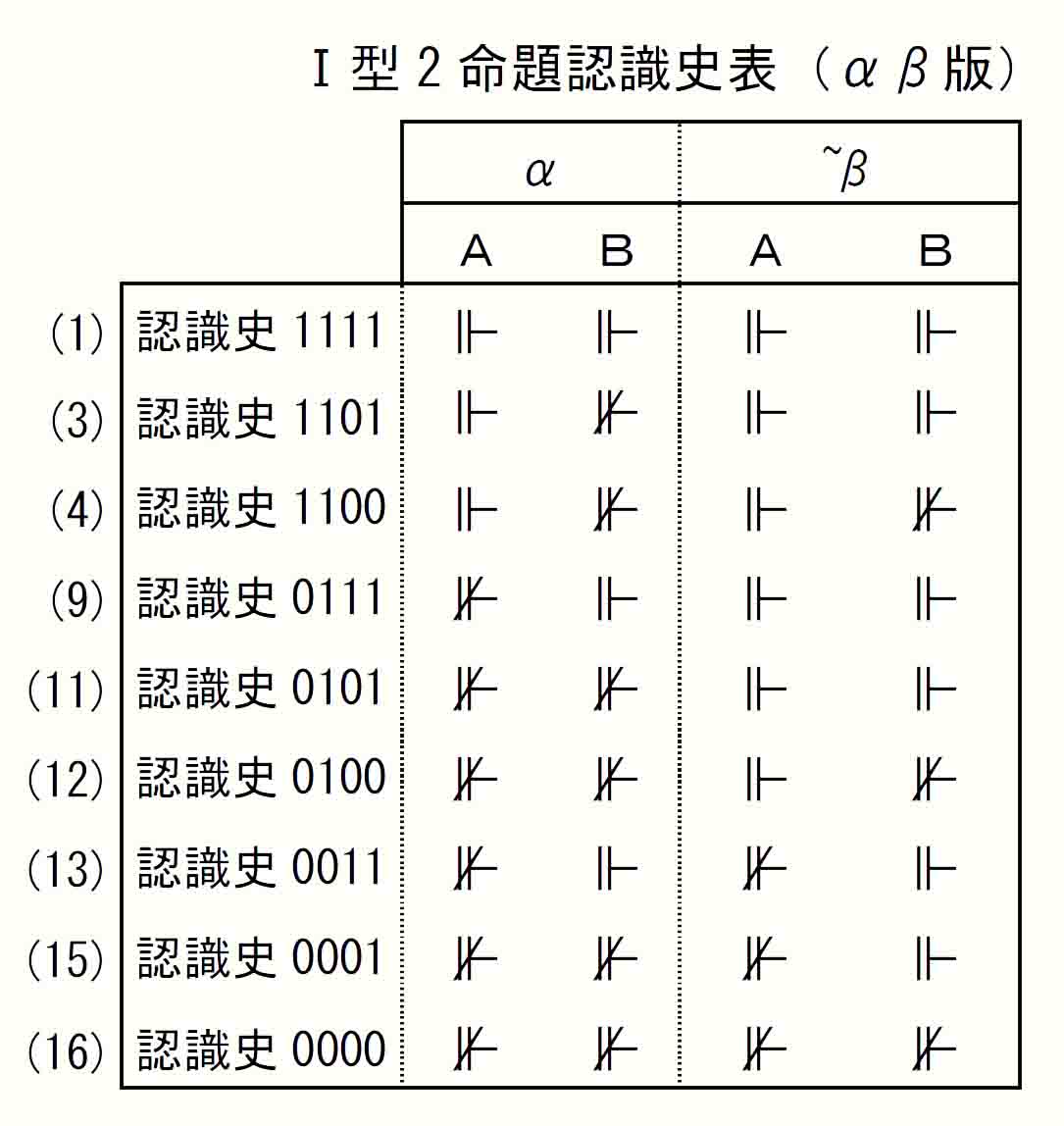
~βで、
[3]a +A、-Bは、認識史1100、0100
[3]b -A、+Bは、認識史0011、0001
に認められる。
これら4つの知識状態のα期がどうであったかを見てみると、
[3]a 認識史1100は、α⊩A、α⊮B
[3]a 認識史0100は、α⊮A、α⊮B
[3]b 認識史0011は、α⊮A、α⊩B
[3]b 認識史0001は、α⊮A、α⊮B
で、[3]aの認識史0100と[3]bの認識史0001は、α期で同じ知識状態を共有している。
ここで、上の「Ⅰ型2命題認識史表」を、α期の知識状態ごとにグループ化した「Ⅰα型2命題認識史表」に変えてみる。
2命題のα期の知識状態のあり方は4通りなので、認識史(13)を(9)の下に移動させて4つのグループにする。
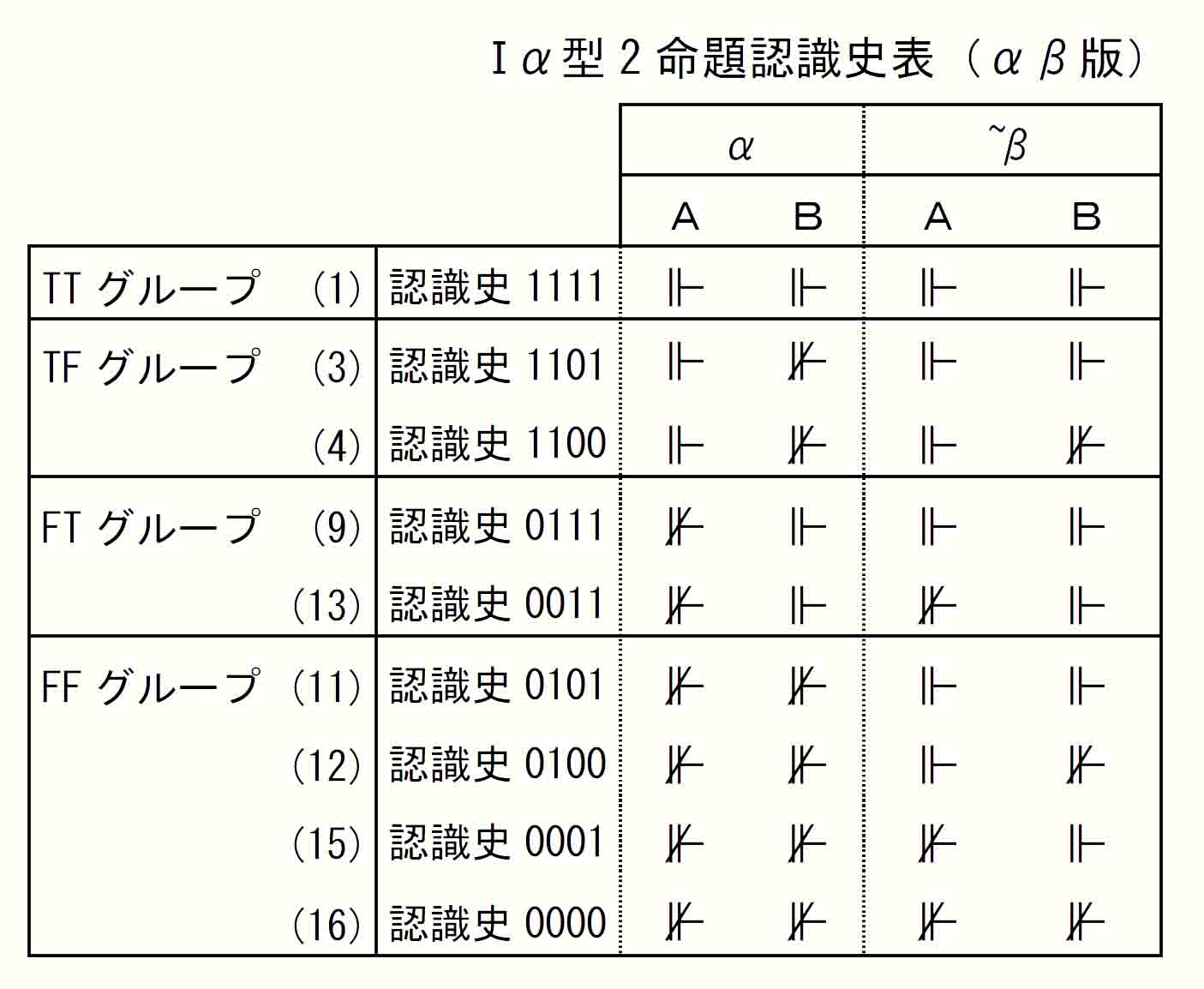
認識史1桁目(A-α期)と3桁目(B-α期)の値をグループ名にするイメージで、上からTT、TF、FT、FFグループとする。
[3]aの認識史0100と[3]bの認識史0001はFFグループで、過去期で同じ知識状態を共有している。一方、[3]a 1100はTFグループ、[3]b 0011はFTグループなので、過去期の知識状態はいずれとも共有しない。
認識史分析はその逆の手順により元の式に遡ることができるものであるので、将来分析から生じた「かつ」関係にある二つの枝先から遡る枝元は一つであり、当然その知識状態は共有されていたことになる。すなわち将来分析から生じた二つの枝は、一つ前には同じ知識状態にいたのでなければならない。
そのため前段階で同じ知識状態FFを共有していた[3]aの認識史0100と[3]bの認識史0001が、[2]の-(A⊃B)、-(B⊃A)を将来分析した際の認識史であったことが分かるのである。つまり、ここでの認識史0100と認識史0001は、認識史FF(認識史0x0x)レベルでは⊮A、かつ、⊮Bという一つの認識史である。
このFF認識史表に、前節で作成した「A⊃Bの証明表」と「B⊃Aの証明表」を横につないで、上の事態を確認してみよう。
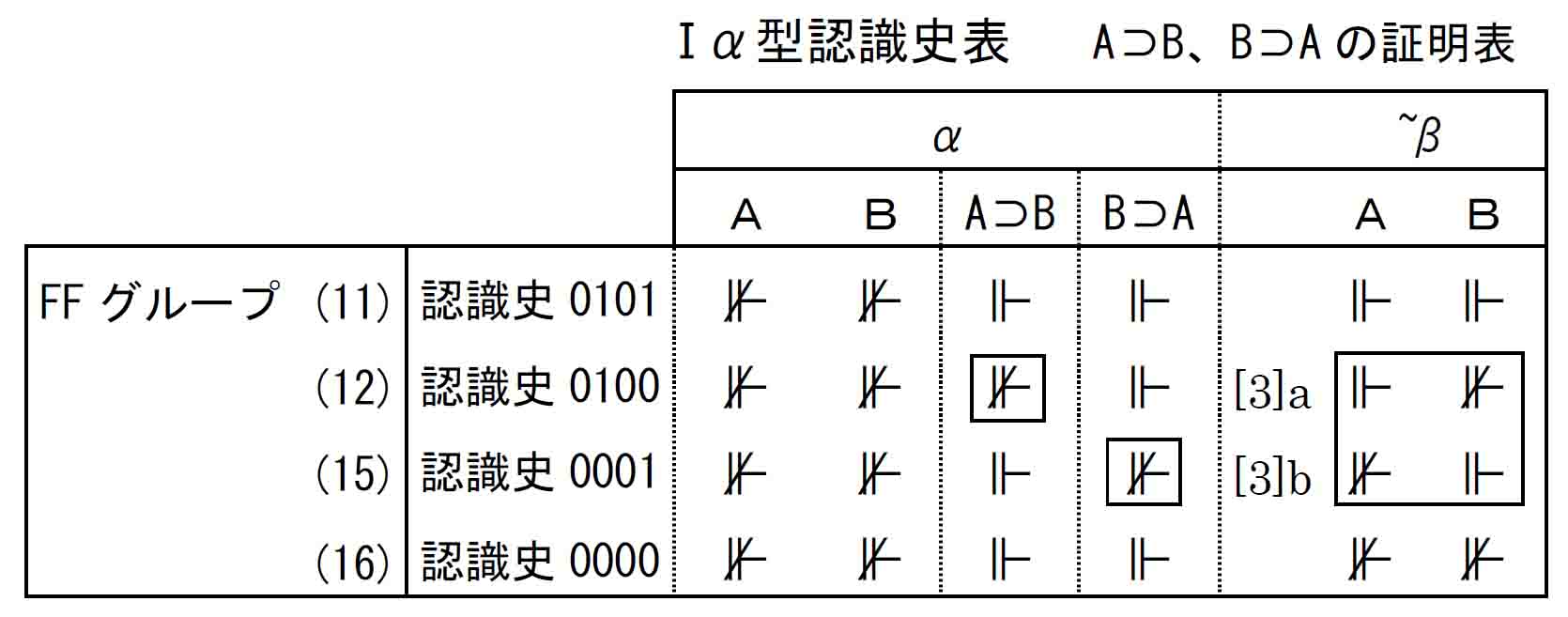
認識史0100α期のA⊃Bは、~β期で⊩A、かつ、⊮Bであるから不証明であることが定まっている。同様に、認識史0001α期のB⊃Aは、~β期で⊩B、かつ、⊮Aであるから不証明であることが定まっている。
これら[3]aと[3]bの~βの知識状態は、α期での同じ知識状態から出発して「かつ」関係として同時に起きているので、認識史0100α期の⊮A⊃Bと認識史0001α期の⊮B⊃Aも「かつ」の関係に置かれる。そして∨式は両辺の証明値が⊮であるときに⊮になるので(-∨の現状分析)、これにより(A⊃B)∨(B⊃A)の非妥当式であることが見てとれる。
このときA⊃BとB⊃Aについて、同時に起きている知識状態とは、通常は、
<1> 認識史0101のA⊃BとB⊃A
<2> 認識史0100のA⊃BとB⊃A
<3> 認識史0001のA⊃BとB⊃A
<4> 認識史0000のA⊃BとB⊃A
の4通りだけである。
しかし、認識史0x0xレベルでは、これら4つの認識史においてA⊃BとB⊃Aのすべての組み合せ16通りが同時に内包されているといえる。その中に、<2>認識史0100のA⊃Bと、<3>認識史0001のB⊃Aの組み合せがあり、これらは共に不証明であるため、この事態が(A⊃B)∨(B⊃A)の非妥当式であることを示しているということである。
こうしてⅠα型証明表は、少なくともプレ線型性について、∨でつながった二つの論理式が、α期の知識状態を同じくするグループの中で、二つとも不証明である知識状態の組み合わせを持つことによって、これを非妥当式として表現しているということができるのである。
ついでに、FFグループ以外のⅠα型証明表を掲げておくと、上の<1>~<4>の組み合わせにおいて、同じグループ内でA⊃BとB⊃Aが共に不証明である組み合わせのないことが確認できる。
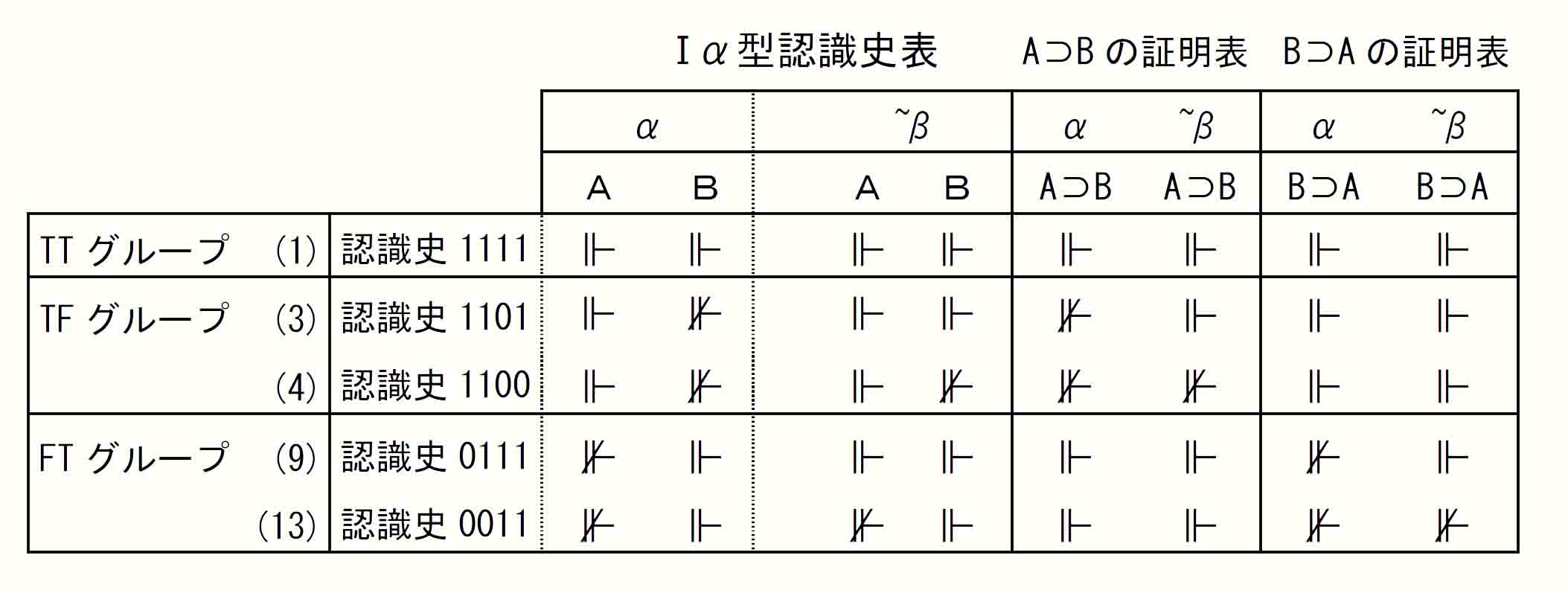
さて、上に見てきたことが、直観主義論理において一番「外」で機能する論理記号が「∨」である非妥当式の場合に必ず機能し、したがってⅠα型証明表がこのタイプの非妥当式を常に適切に表示するのかについては確認していない。
また、Ⅰα型証明表はⅠ型証明表の認識史行を入れ替えただけのものなので、前節でみた各論理式の定理/非定理を前節で見たとおりに再現することは明らかである。したがって、ここで扱ったプレ線型性以外の式について、Ⅰα型証明表を用いての再確認は不要である。
上の考察を通じて、Ⅰ型証明表で非定理が正しく表現されない理由の一端を知ることができた。プレ線型性と同じく「∨」を最終機能とする非妥当式A∨¬Aの場合は、その非妥当性は単一の認識史01に表れていたが、直観主義論理の非妥当式は、その非妥当性が必ずしも単一の認識史上に表れるのではなく、認識史途上からの枝分かれによる複数の認識史が同時に起こり、それによって非妥当が実現されることがあるということである。