| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (23)
Hard study 5-5-1 クリプキ系Ⅰ型証明表
頁内目次
(1)「証明表」の行く末
(2)「Ⅰ型証明表」の作成
■ 直観主義論理∧の証明表
■ 直観主義論理∨の証明表
■ 直観主義論理⊃の証明表
■ 直観主義論理¬の証明表
(3) Ⅰ型証明表による定理・非定理の確認
No. 1 非定理 A∨¬A 排中律
No. 2 非定理 ¬¬A⊃A 二重否定除去
No. 3 非定理 (¬B⊃¬A)⊃(A⊃B) 反対偶律
No. 4 非定理 (A⊃B)⊃(¬A∨B) 古典論理条件法(1)
No. 5 定理 (¬A∨B)⊃(A⊃B) 古典論理条件法(2)
No. 6 非定理 ((A⊃B)⊃A)⊃A パース律
No. 7 非定理 A⊃(B∨¬B)
No. 8 定理 ¬(A∨B)⊃(¬A∧¬B) ド・モルガン律9(1)a
No. 9 定理 (¬A∧¬B)⊃¬(A∨B) ド・モルガン律9(1)b
No.10 非定理 ¬(A∧B)⊃(¬A∨¬B) ド・モルガン律9(2)a
No.11 定理 (¬A∨¬B)⊃¬(A∧B) ド・モルガン律9(2)b
No.12 非定理 (A⊃B)∨(B⊃A) プレ線型性
(1)「証明表」の行く末
Hard study 5-2-4の冒頭で触れた「直観主義論理の意味論を真理表で表すことはできない」ことについて確認したい。それはどのような事態なのか。
野矢茂樹『論理学』には「直観主義論理の意味論を真理表で表すことはできません」と書かれている。一方で、同書ではその2頁後に「分子式の分析」が行われており、これは直観主義論理クリプキ意味論の規則を用いて、基本の結合子に関する分子式(A∧B、A∨B、A⊃B、¬A)の証明値を一つ一つ得ていこうとする作業である。これを続ければ、古典論理の真理表に相当する直観主義論理の真理表(証明表)が完成することは自明と思われる。しかしそれは不可能だというのである。
それは、その「分子式の分析」作業によって証明表のマスをすべて埋めることはできないことを意味しているのだろうか。つまり、正確には、直観主義論理の証明表は『論理学』やHard study 5-2-4で見てきたような「頭初期」と「後続期」という二つの知識状態からなるものではなく、「後続期」に続くような無限個の期、あるいは「頭初期」と「後続期」の間の分割による無限個の期から構成されているので、これら無限にあるマスを証明値で満たすことはできないことをいうものなのか。
あるいはそういうことではなく、証明表自体は有効だが、なにか他の理由によって、この証明表は直観主義論理を正しく表現できないということであるのか。
これについては、直観主義論理のいま一つの意味論であるハイティング代数の理解を得てからさらに検討することとしたいが、ここでは、これまでに行ってきた「分子式の分析」すなわち「証明表」の作成を進めていくとその行く末がどうなるかを見てみたい。それは、直観主義論理における定理・非定理を正しく表現するものとなるのか。
古典論理で定理であって直観主義論理で非定理である論理式は多数ある。ここではよく知られているその種の論理式8個とそれに関連した定理式(後述)について調べてみる。
結論を先に述べると、古典論理の定理の内、直観主義論理で非定理となる論理式8個について、クリプキ意味論から作成した証明表は、そのうちの6個を非妥当式として適切に表現する。
ただド・モルガン則の一つである¬(A∧B)⊃(¬A∨¬B)と、プレ線型性と呼ばれる(A⊃B)∨(B⊃A)について、以下で作成する証明表はこれを妥当式として表現してしまう。
古典論理で定理であり、直観主義論理でも定理である論理式に関しては、ここで見た範囲では、この証明表ですべて妥当式として表現されている。
この事態がなぜであるのかという疑問を早く解きたいところだが、その解決は易しくはなさそうなのでいったん置いておき、とりあえず「分子式の分析」を進めて、先に作成した¬以外の論理記号について「2命題証明表」を作成してみよう。
なお、この証明表を「Ⅰ(イチ)型証明表」と呼ぶ。これが後に、同等であることが確認されたハイティング代数のI(アイ)形3値モデルに関係させた名前のようになったのは単なる偶然である。
(2)「Ⅰ型証明表」の作成
認識史は、1命題の場合、Hard study 5-2-4に示した「直観主義論理の¬Pの証明表」の通り3行の認識史となる。その認識史をα、~βでの原子命題の証明値に関連づけて、それぞれ認識史11、01、00とした。
2命題になると、2証明値^(2命題×2期)=16行の認識史となるが、意味論Ⅱ(1)により除外が発生し(Hard study 5-2-3参照)9行の認識史に落ち着く。
各行の認識史は、先頭からA-α期、A-~β期、B-α期、B-~β期の証明値を1、0で置き換えた4桁の数字で表す。したがって認識史が4桁の場合は、先頭の2桁がAの認識史を表し、末尾の2桁がBの認識史を表す。認識史が2桁の場合は、Aの認識史である場合とBの認識史である場合がある。
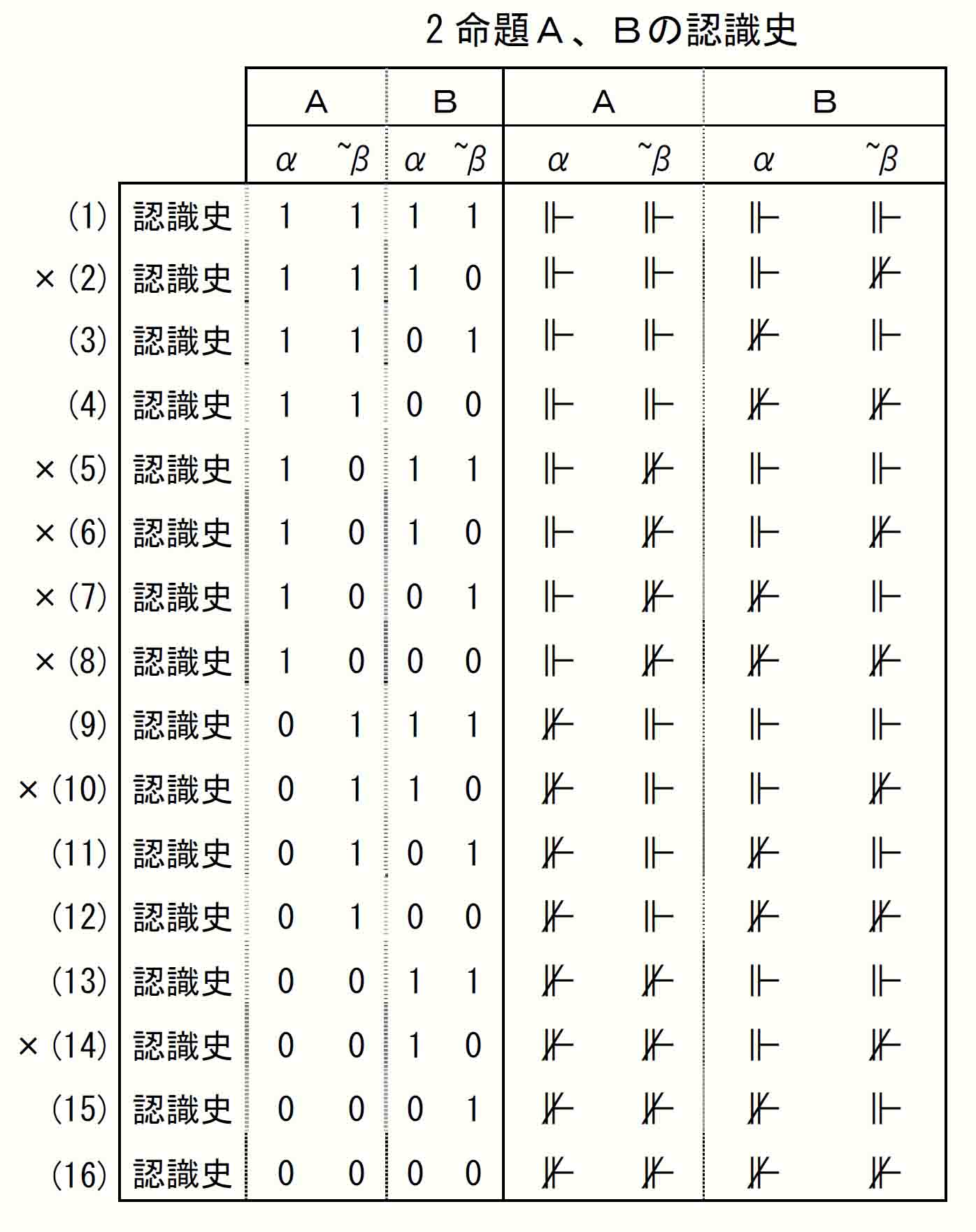
上で、×印の行は認識史に10(証明から不証明)が含まれるため意味論Ⅱ(1)により除外される。したがって2命題A、Bの認識史は以下。
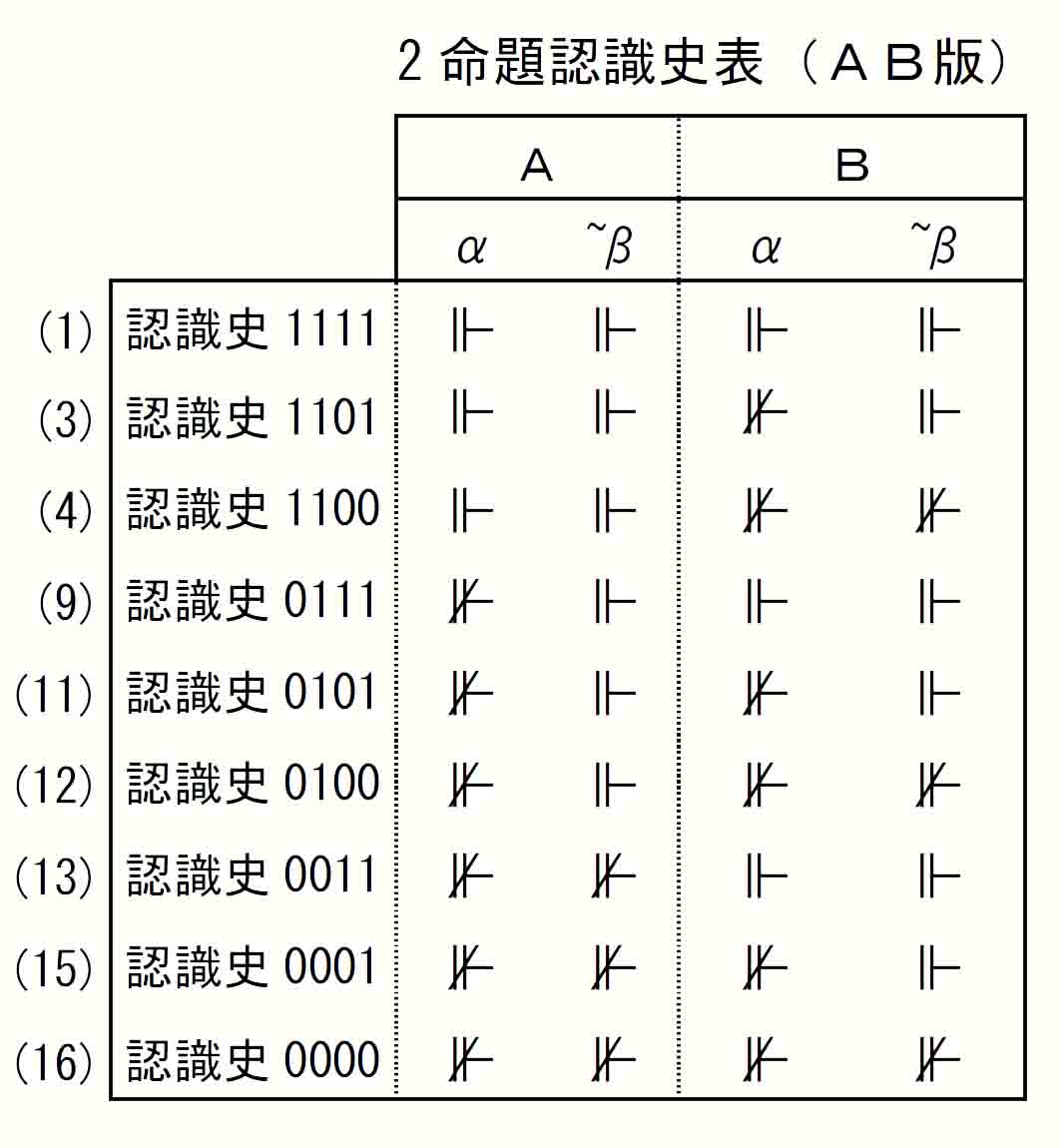
列を入れ替えると期を優先した認識史表となる。
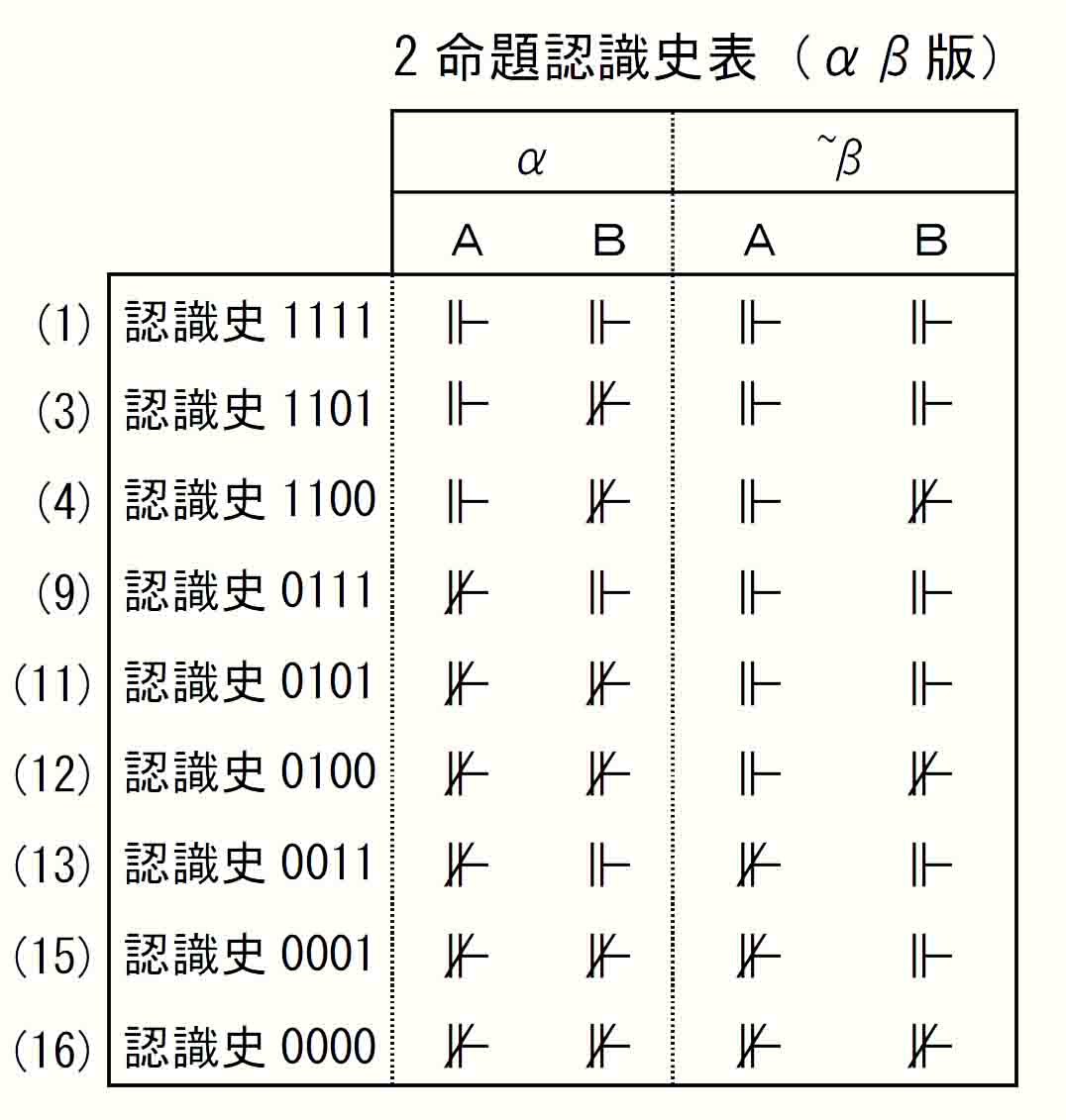
以下に、クリプキ意味論Ⅱ(2)~(5)の読み替えと証明表を示す。(¬についても Hard study 5-2-2 から再録。)
意味論Ⅱ(2)~(5)の読み替えは、証明済の論理記号の除去と不証明の論理記号の除去、証明済の論理記号の導入と不証明の論理記号の導入という4つの読み替えからなっている。
「すべての認識史」とは証明表の縦方向に展開されている9行の認識史を指し、「すべての期」「すべての後続期」「後続期すべて」などは各認識史が横方向に展開するα期と~β期の2列を指す。
Hard study 5-2-2 では「ある期」をα期のこととしたが、以下では「ある期」をα期または~β期いずれかの1列を指すものとする。
証明表の~β期はα期を含まないが、意味論読み替えでの「後続期」や「β」はα期を含んでいる。
∧、∨、⊃、¬の証明表を「基本証明表」と呼ぶ。「基本証明表」は便宜のためαβ版の形式とする。(認識史4桁の数字はAB版のまま保たれることに注意。)
■直観主義論理∧の証明表
意味論Ⅱ(2) α⊩A∧B ⇔ α⊩Aかつα⊩B
(ワ) Ⅱ(2)→方向(証明済の∧の除去則)
αで⊩A∧Bのとき、αで⊩Aかつ⊩B
ある期でA∧Bが証明されている認識史では、同期でAが証明されかつBも証明されている
(カ) Ⅱ(2)→方向裏(不証明の∧の除去則)
αで⊮A∧Bのとき、αで⊮Aまたは⊮B
ある期でA∧Bが証明されていない認識史では、同期でAが不証明かまたはBが不証明である
(ヨ) Ⅱ(2)←方向(証明済の∧の導入則)
αで⊩Aかつ⊩Bの場合、αで⊩A∧B
ある期でAが証明されかつBも証明されている認識史では、同期でA∧Bが証明されている
(タ) Ⅱ(2)←方向裏(不証明の∧の導入則)
αで⊮Aまたは⊮Bの場合、αで⊮A∧B
ある期でAが不証明またはBが不証明である認識史では、同期でA∧Bは不証明である

∧の各証明値の計算は、∧導入則である(ヨ)と(タ)から容易に行えるので省略。例えば、(ヨ)「ある期でAが証明されかつBも証明されている認識史では、同期でA∧Bが証明されている」からは、認識史1111のα、~βおよび、認識史1101、0111、0101の~βの証明値が得られることが確認できる。
前節に述べたように、直観主義論理の∧の証明値は、同期に関して古典論理の演算から得られる値と同じである。(古典論理の∧の真理表は『論理学』p.33参照)
■直観主義論理∨の証明表
意味論Ⅱ(3) α⊩A∨B ⇔ α⊩Aまたはα⊩B
(リ) Ⅱ(3)→方向(証明済の∨の除去則)
αで⊩A∨Bのとき、αで⊩Aまたは⊩B
ある期でA∨Bが証明されている認識史では、同期でAが証明されているかまたはBが証明されている
(ヌ) Ⅱ(3)→方向裏(不証明の∨の除去則)
αで⊮A∨Bのとき、αで⊮Aかつ⊮B
ある期でA∨Bが証明されていない認識史では、同期でAが不証明でありかつBも不証明である
(ル) Ⅱ(3)←方向(証明済の∨の導入則)
αで⊩Aまたは⊩Bのとき、αで⊩A∨B
ある期でAが証明されているかまたはBが証明されている認識史では、同期でA∨Bが証明されている
(ヲ) Ⅱ(3)←方向裏(不証明の∨の導入則)
αで⊮Aかつ⊮Bの場合、αで⊮A∨B
ある期でAが不証明でかつBも不証明である認識史では、同期でA∨Bは不証明である
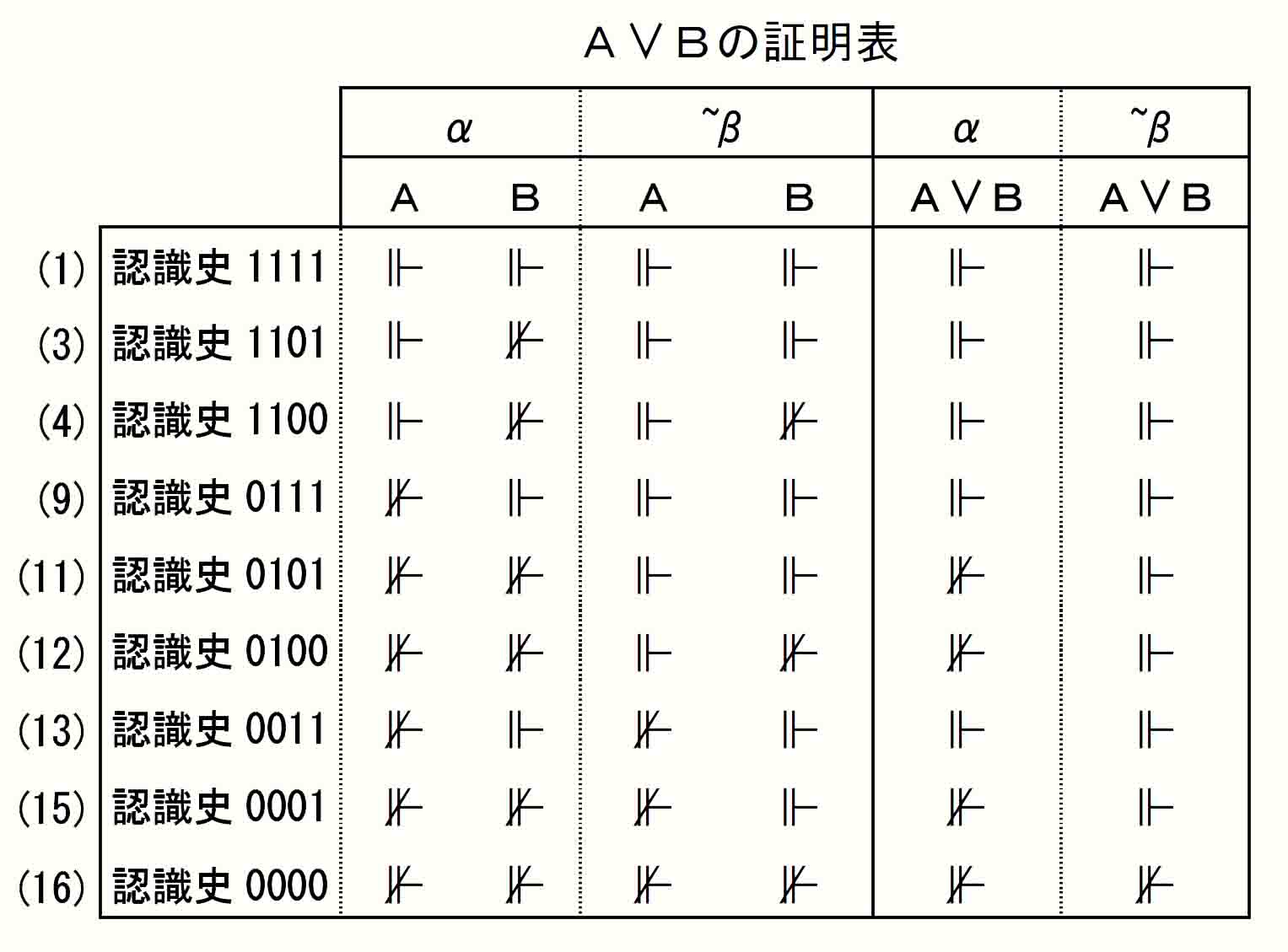
証明値の計算は省略。直観主義論理の∨の証明値は、同じ期に関して古典論理の演算から得られる値と同じ。(古典論理の∨の真理表はEasy Study 2-2)
■直観主義論理⊃の証明表
意味論Ⅱ(4) α⊩A⊃B ⇔ すべてのβについて(⊩Aのとき⊩B)
(ホ)Ⅱ(4)→方向(証明済の⊃の除去則)
α⊩A⊃Bのとき、すべてのβについて⊮Aまたは⊩B
αで⊩A⊃Bが成立している認識史で次が成立している。その認識史のすべての期の各々において、⊮Aであるかまたは⊩Bである、が成立している
(ヘ)Ⅱ(4)→方向裏(不証明の⊃の除去則)
α⊮A⊃Bのとき、あるβで⊩Aかつ⊮B
αで⊮A⊃Bとなっている認識史で次が成立している。その認識史に⊩Aかつ⊮Bが成立している期がある。
(ト)Ⅱ(4)←方向(証明済の⊃の導入則)
すべてのβで⊮Aまたは⊩Bのとき、αで⊩A⊃B
⊮Aであるか⊩Bである、がすべての期で成立している認識史では、αで⊩A⊃Bが成立している。
(チ)Ⅱ(4)←方向裏(不証明の⊃の導入則)
あるβで⊩Aかつ⊮Bのとき、αで⊮A⊃B
いずれかの期で⊩Aかつ⊮Bが成立している認識史においては、αで⊮A⊃Bが成立している。

直観主義論理の⊃の証明値では○印の箇所で、古典論理の同期の演算から得られる値とは異なった証明値となっている。認識史0100ではα⊮A、α⊮Bであるから、古典論理の計算では前件が偽の場合A⊃Bは真なので証明値は⊩になる。
しかし意味論(チ)は「あるβで⊩Aかつ⊮Bのとき、αで⊮A⊃B」と定めており、認識史0100では~βでこれが成立しているのでα⊮A⊃Bとなる。直観主義論理においては、前件真、後件偽のパターンがどこかの期に存在するとき、α期の⊃は偽である。
■直観主義論理A⊃Bの証明値
認識史1111α
すべての期で⊩B。(ト)より、α⊩A⊃B
認識史1111~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
認識史1101α
αで⊩Aかつ⊮B。(チ)よりα⊮A⊃B
認識史1101~β
⊃の導入則(ト)、(チ)はαでの⊃の証明値を述べるもので~βでのA⊃Bの証明値を述べていない。また、α期の⊃式が不証明である場合に適用できる意味論規則はない。しかしこれまでの考察で、直観主義論理の特異性は証明値に変遷の可能性があるα期に表れていることから、証明値の最終状況である~β期での直観主義論理は古典論理と同じふるまいをするものとして理解できる(Hard study 5-3-3 終わり参照)。そこで、認識史1101では~β⊩A、~β⊩Bであり、後件Bが最終的に証明済の事態にあることから、古典論理の規則を適用し~β⊩A⊃B
認識史1100α
すべての期で⊩Aかつ⊮B。(チ)によりα⊮A⊃B
認識史1100~β
認識史1101~βと同様に、認識史1100~βの証明値を述べる規則はないが、~βで⊩Aかつ⊮Bが成立しているので~β⊮A⊃B
認識史0111α
すべての期で⊮Aまたは⊩Bが成立しているので、(ト)によりα⊩A⊃B
認識史0111~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
認識史0101α
すべての期で⊮Aまたは⊩Bが成立しているので、(ト)によりα⊩A⊃B
認識史0101~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
認識史0100α
~βで⊩Aかつ⊮B。(チ)よりα⊮A⊃B
認識史0100~β
認識史1101~βと同様に、認識史0100~βの証明値を述べる規則はないが、~βで⊩Aかつ⊮Bが成立しているので~β⊮A⊃B
認識史0011α
すべての期で⊮A。(ト)によりα⊩A⊃B
認識史0011~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
認識史0001α
すべての期で⊮A。(ト)によりα⊩A⊃B
認識史0001~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
認識史0000α
すべての期で⊮A。(ト)によりα⊩A⊃B
認識史0000~β
α⊩A⊃Bなので意味論Ⅲより~β⊩A⊃B
■直観主義論理¬の証明表
(Hard study 5-2-4から命題記号を変えて再録)
意味論Ⅱ(5) α⊩¬A←→すべてのβで⊮A
(イ) Ⅱ(5)→方向(証明済の¬の除去則)
αで⊩¬Aのとき、すべてのβで⊮A
ある期で命題Aの否定が証明された場合、後続期で肯定は証明されない
(ロ) Ⅱ(5)→方向裏(不証明の¬の除去則)
αで⊮¬Aのとき、あるβで⊩A
ある期で命題Aの否定が証明されていない場合、後続期のどこかで肯定が証明される
(ハ) Ⅱ(5)←方向(証明済の¬の導入則)
すべてのβで⊮Aのときαで⊩¬A
すべての期で命題Aの肯定が証明されない場合、頭初期で否定が証明されている
(ニ) Ⅱ(5)←方向裏(不証明の¬の導入則)
あるβで⊩Aのときαで⊮¬A
後続期のいずれかで命題Aの肯定が証明された場合、頭初期で否定は証明されていない

証明値計算はHard study 5-2-4に記載。
○印箇所の証明値が、古典論理の演算から得られる値とは異なっている。古典論理ではAが偽であるなら¬Aは真。しかし認識史01ではαでAが不証明だが、¬Aもαで不証明である。Hard study 5-3-1に述べたが、直観主義論理ではAも¬Aも真偽不明であるという事態が取り入れられている。
(3) Ⅰ型証明表による定理・非定理の確認
以上で、直観主義論理の基本証明表が揃ったので、以下8個の非定理式と、これに関連した4個の定理式の証明値を見ていく。
手順はEasy Study 2-2で確認した古典論理の「真理値分析」と同じで、論理式のα期、~β期の証明値パターンを、上の基本証明表から探し出して分子式の証明値を得ていく作業を繰り返す。
■No.1 非定理 A∨¬A 排中律
Hard study 5-2-4で作成済。Ⅰ型証明表で非妥当式として表示される。
■No.2 非定理 ¬¬A⊃A 二重否定除去
Hard study 5-2-4で作成済。Ⅰ型証明表で非妥当式として表示される。
■No.3 非定理 (¬B⊃¬A)⊃(A⊃B) 反対偶律

¬Aの証明表と¬Bの証明表を組み合わせて¬A、¬Bの認識史を得る。
¬Aの認識史はAの認識史由来であり、¬Bの認識史はBの認識史由来の認識史であるので、二つの認識史は独立したものである。そのため¬A、¬Bの認識史は、二つの認識史のすべての組み合せ(直積)となる。

続いて認識史を4桁にまとめ、⊃の前件、後件を考慮して列を入れ替えたものをαβ版の要領で作成する。各認識史の証明値パターンを、⊃の証明表(αβ版)の原子式の証明値パターンと照合して、合致する認識史の分子式の証明値を¬B⊃¬Aの証明値とする。
例えば、認識史0100の¬B、¬Aの証明値は左から⊩、⊮、⊩、⊮。これをA⊃Bの証明表に求めると認識史1100に該当するので、認識史1100のA⊃Bの証明値α⊮、~β⊮を¬B⊃¬Aの証明値とする。

次に、A⊃Bの基本証明表を、¬B⊃¬Aの証明表に結合して、(¬B⊃¬A)⊃(A⊃B)の証明値を得る。¬B⊃¬AとA⊃Bは、いずれも先の「2命題認識史表」を認識史の由来としているので、結合にあたっては同じ認識史同士を1対1の関係で結合すればよい。¬B⊃¬AとA⊃B間で列入れ替えを行いαβ版とする。
⊃(A⊃B)_ProofMatrix.jpg)
認識史1101では左から⊩、⊮、⊩、⊩。これをA⊃Bの証明表に求めると認識史1101に該当するので、認識史1101のA⊃Bの証明値α⊮、~β⊩を(¬B⊃¬A)⊃(A⊃B)の証明値とする。 これにより認識史1101α期で⊮となり、妥当式ではないことが示されている。
■No.4 非定理 (A⊃B)⊃(¬A∨B) 古典論理条件法(1)
¬Aの3行認識史とBの3行認識史を組み合せて¬A、Bの9行の認識史を得る。


⊃(¬A∨B)_ProofMatrix.jpg)
認識史0101α期で⊮となり、妥当式ではないことが示されている。
■No.5 定理 (¬A∨B)⊃(A⊃B) 古典論理条件法(2) No.4の逆
⊃(A⊃B)_ProofMatrix.jpg)
すべての認識史のすべての期で⊩であり、妥当式であることが示されている。
■No.6 非定理 ((A⊃B)⊃A)⊃A パース律
(A⊃B)⊃Aのように、前件がAB2命題、後件がA1命題の論理式では、2命題A⊃Bの認識史4桁の前2桁(A⊃BのAの認識史部分)と、Aの認識史2桁を対応させる。
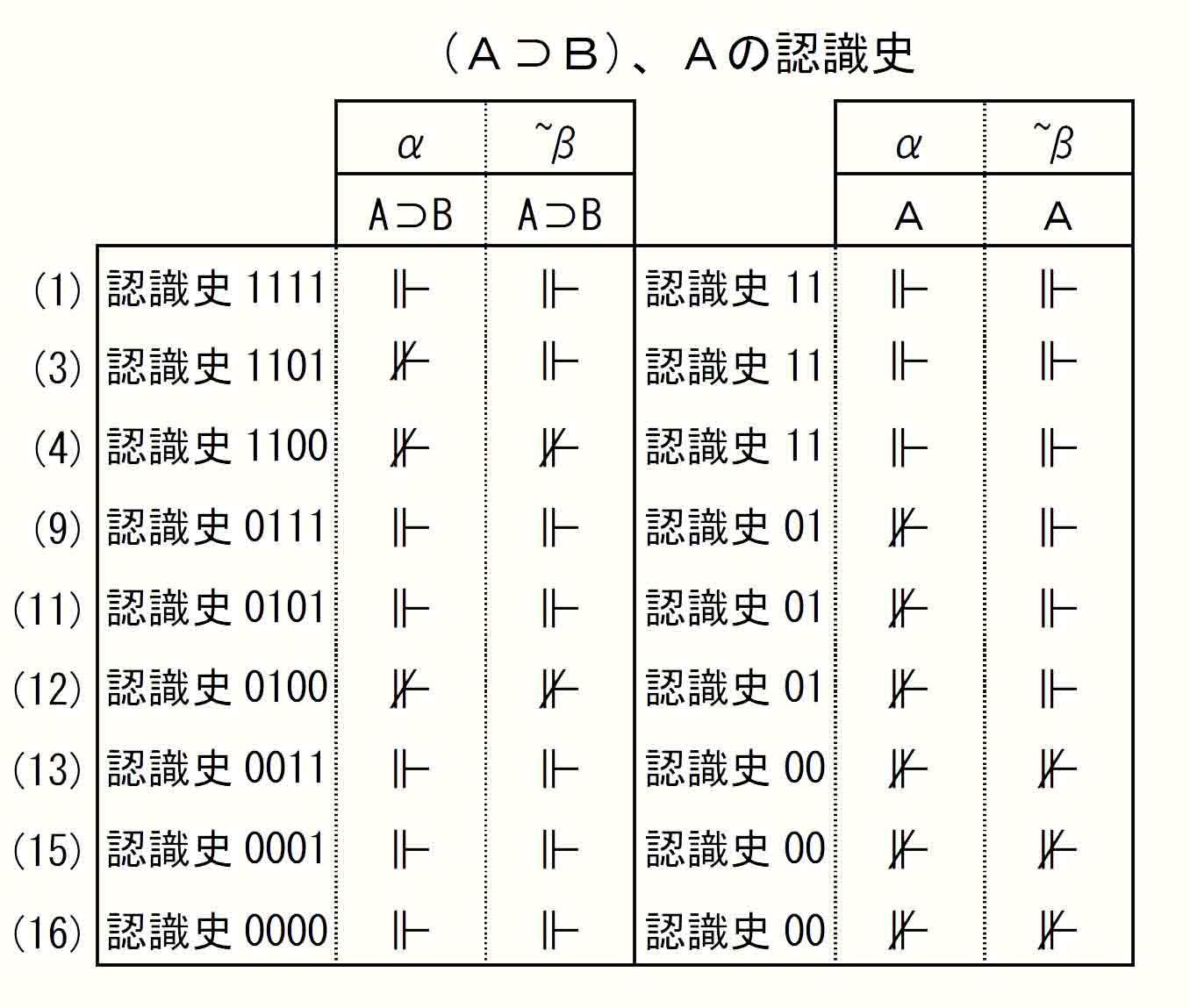
⊃A_ProofMatrix.jpg)
⊃A)⊃A_ProofMatrix.jpg)
認識史0100α期で⊮となり、妥当式ではないことが示されている。
■No.7 非定理 A⊃(B∨¬B)
¬Bの認識史はB由来なので、B、¬Bの認識史は直積を行わず、以下の通り。(¬Aの証明表と同じ)


A、(B∨¬B)の認識史は、A、Bの認識史のすべての組み合せ。
_ProofMatrix.jpg)
_ProofMatrix.jpg)
認識史1101α期で⊮となり、妥当式ではないことが示されている。
■No.8 定理 ¬(A∨B)⊃(¬A∧¬B) ド・モルガン律9(1)a 『論理学』p.70
_ProofMatrix.jpg)

⊃(¬A∧¬B)_ProofMatrix.jpg)
すべての認識史のすべての期で⊩であり、妥当式であることが示されている。
■No.9 定理 (¬A∧¬B)⊃¬(A∨B) ド・モルガン律9(1)b No.8の逆 『論理学』p.70
No.8で「¬(A∨B)の証明表」と「¬A∧¬Bの証明表」の証明値は同型。
No.9の(¬A∧¬B)⊃¬(A∨B)は、No.8の前件と後件を入れ替えたもの。⊃において前件と後件の証明値が同じであるとき、これを入れ替えても同じ結果となることは明らか。
したがってNo.9の(¬A∧¬B)⊃¬(A∨B)は、No.8と同様に妥当式として正しく表示されている。
■No.10 非定理 ¬(A∧B)⊃(¬A∨¬B) ド・モルガン律9(2)a 『論理学』p.182
_ProofMatrix.jpg)

⊃(¬A∨¬B)_ProofMatrix.jpg)
すべての認識史のすべての期で⊩であり妥当式として示されている。しかし¬(A∧B)⊃(¬A∨¬B)は直観主義論理において非定理である。Ⅰ型証明表はこれを示すことができていない。
■No.11 定理 (¬A∨¬B)⊃¬(A∧B) ド・モルガン律9(2)b 『論理学』p.183
No.10の「¬(A∧B)の証明表」と「¬A∨¬Bの証明表」の証明値は同型。
No.11は、No.10の前件と後件を入れ替えたもの。⊃において前件と後件の証明値が同じであるとき、それを入れ替えても同じ結果であることは明らか。
したがってNo.11(¬A∨¬B)⊃¬(A∧B)が妥当式として示されることは明らか。No.11は定理なのでⅠ型証明表はこれを正しく表示している。
■No.12 非定理 (A⊃B)∨(B⊃A) プレ線型性
_ProofMatrix.jpg)
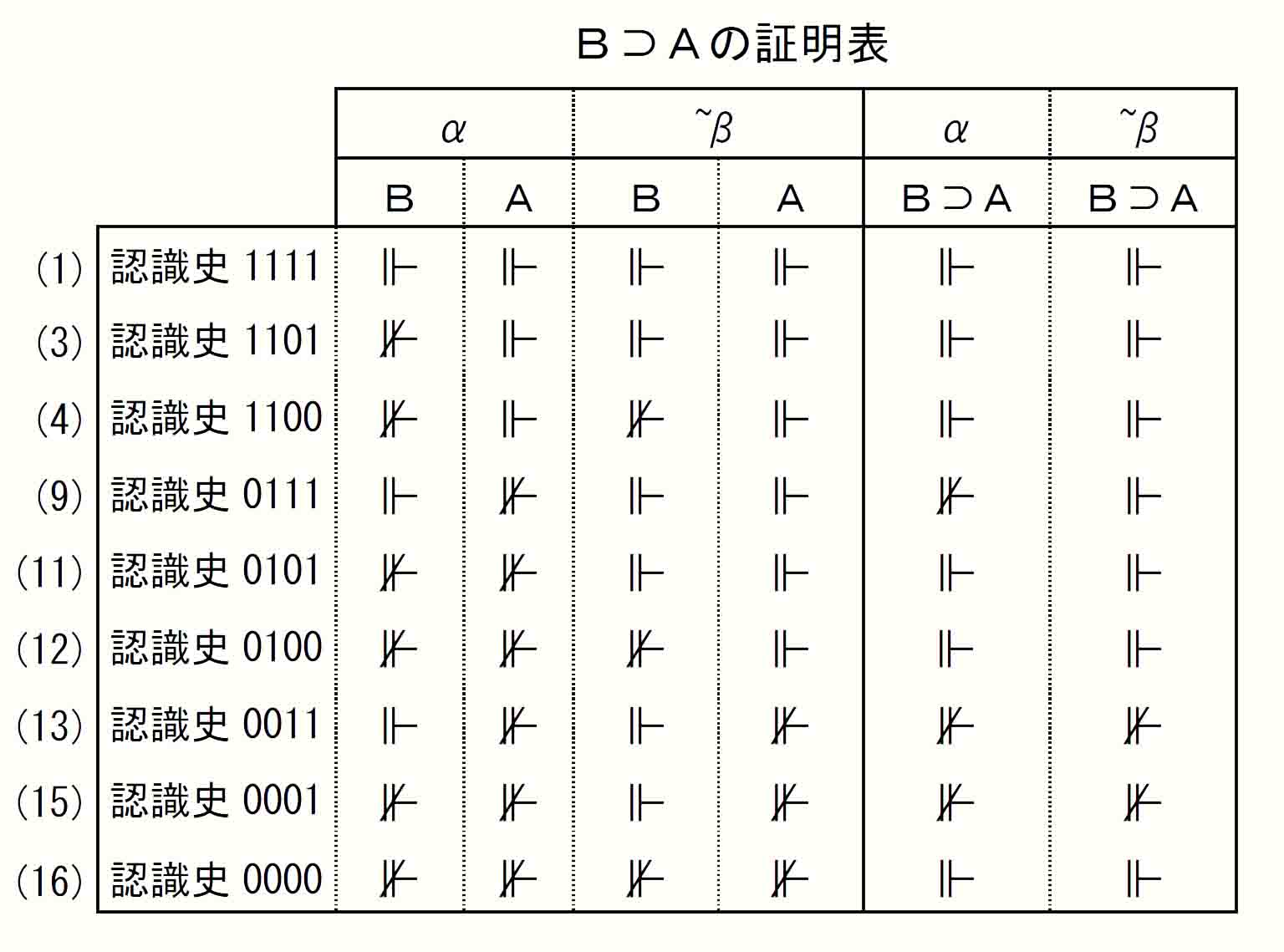
∨(B⊃A)_ProofMatrix.jpg)
Ⅰ型証明表は「プレ線型性」式を非妥当式として表現しない。しかし次節で、「認識史分析」を手がかりとしてⅠ型証明表の見方を工夫することで、「プレ線型性」の非定理性を捉えることができることを確認する。