| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (13)
Hard study 5-2-4 「証明表」
しかし、疑問はさらに増えている。意味論のどこに拒否が仕込まれているのだろうか。そして、意味論と構文論間の矛盾と見える事柄は、結局、どう理解すべきなのか。これを理解するために「証明表」の全行に証明値を入れてみよう。
ところでこの「証明表」は、古典論理の「真理表」に相当するものだが、同書には直観主義論理の意味論を「真理表で表わすことはできませんけど」(p.173)と書かれていて、古典論理の「真理表」に相当するようなものは示されていない。
もちろん証明値⊩、⊮を論理式の肯定、否定とする直観主義論理は、真理値1、0を論理式の肯定、否定とする古典論理とは異なるので、この意味で、直観主義論理の意味論を古典論理の真理表で表わすことができないのは当然のことだが、「真理表で表わすことはできません」というのはその意味で言われているのではないだろう。真理値であれ証明値であれ、ともかく古典論理の真理表のような原子命題の値から構成された表で直観主義論理の意味論を示すことはできない、というのがそこで言われていることの主旨と思われる。
ただし、同書p.175「分子式の分析」では、認識史K0(認識史01)について、いくつかの論理式の証明値を求めている。そこで求められている証明値は認識史01に関してだけであり、また頭初期α、後続期~βのうち頭初期だけの場合もあるが、この「分子式の分析」を、認識史11、01、00の頭初期α、後続期~βすべてについて行うことができれば「証明表」が得られることは確かである。
また、直観主義命題論理では古典命題論理と同じように「妥当式か否かを機械的に示す方法(認識史分析)」があるということなので(p.178)、この点からも「真理表」に代わる「証明表」のような固定値を持つ表で、意味論(ここでは「直観主義論理の意味論」Ⅱの部分)を別様に表現することが可能であるように思われる。
しかしながら「分子式の分析」に、∧、∨、⊃、¬の4つの結合子のうち⊃だけ、証明値の分析が書かれていない点が気がかりである。⊃の分析が慎重に避けられており、このところに「真理表で表わすことはできませんけど」ということの真意が暗示されている可能性も考えられる。
ここに示す「証明表」は、1命題Pに否定子と結合子を加えた分子式(論理式)、すなわち排中律と二重否定除去則に関するものだけであり、これについては以下に見るとおり、直観主義論理の状況をよく表現しているといえる。しかし2命題A、Bにおける論理式でも同様に「証明表」が作成でき、かつ、直観主義論理の定理を表現するものであるのかは確認できていない。
例えば、同書p.168問題77に挙げられている、ド・モルガンの法則の一つである¬(A∧B)⊃(¬A∨¬B)が、直観主義論理で非定理であるのに従って、この「証明表」でも妥当式とならないことが表現され、その逆の(¬A∨¬B)⊃¬(A∧B)が、直観主義論理で定理であるのに従って、この「証明表」で妥当式として表現される、などの確認は行えていないので、以下の「証明表」は、とりあえずは直観主義論理を理解するための便宜的な方法として理解していただきたい。(これについての見解はEasy study 5-4-5に「追記」として掲載する予定。2021年2月記。→ 2024年2月、Hard study 5-5-1 ~ 5-5-4として追記。)
さて、結構な留保付きではあるが、以下では先の「証明表」を使って、直観主義論理の理解を得ていこう。排中律では¬P、二重否定除去則では¬¬Pが出てくるので、まずこれらの証明値を確定してみる。
与えられているのは、Easy study 5-2-1の「直観主義論理の意味論Ⅰ~Ⅲ」と、Hard study 5-2-2での意味論Ⅱ(5)の読み替え(イ)(ロ)(ハ)(ニ)、および下のPの認識史である。(以下、認識史10は除外)
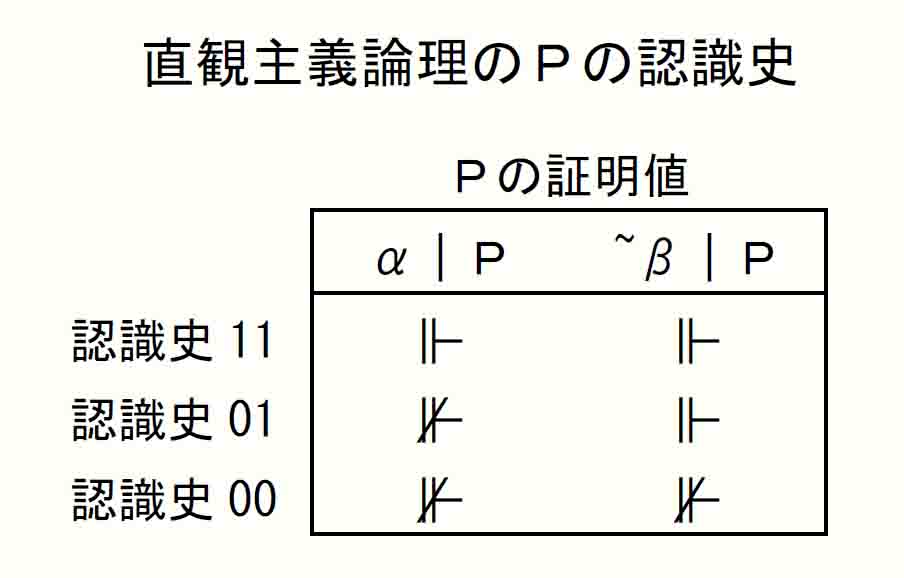
■直観主義論理¬Pの証明値
認識史11α
α⊩Pなのでα⊮¬P
認識史11~β
~β⊩Pなので~β⊮¬P
認識史01α
意味論規定Ⅱ(5)←方向により、すべてのβで⊮Pならばαで⊩¬P
すなわち、α⊮Pかつ~β⊮Pである認識史のとき(に限り)、αで⊩¬P
※Ⅱ(5)は同値(双条件)なので、Ⅱ(5)←方向の「ならば」は「そのときに限り」の意味。Hard study 5-2-3 注[4]参照。
ところが認識史01はα⊮Pかつ~β⊩Pなので、αで⊩¬Pとはならない。
すなわち、αでは⊮¬P
認識史01~β
認識史01では~β⊩P
ゆえに、~β⊮¬P
認識史00α
意味論規定Ⅱ(5)←方向により、すべてのβで⊮Pならばαで⊩¬P
すなわち、α⊮Pかつ~β⊮Pの認識史のとき、αで⊩¬P
認識史00はα⊮Pかつ~β⊮Pなので、αで⊩¬P
認識史00~β
認識史00ではα⊩¬P
ゆえに意味論Ⅱ(1)より、~β⊩¬P
以上から、直観主義論理の¬Pの証明表は次のようになる。
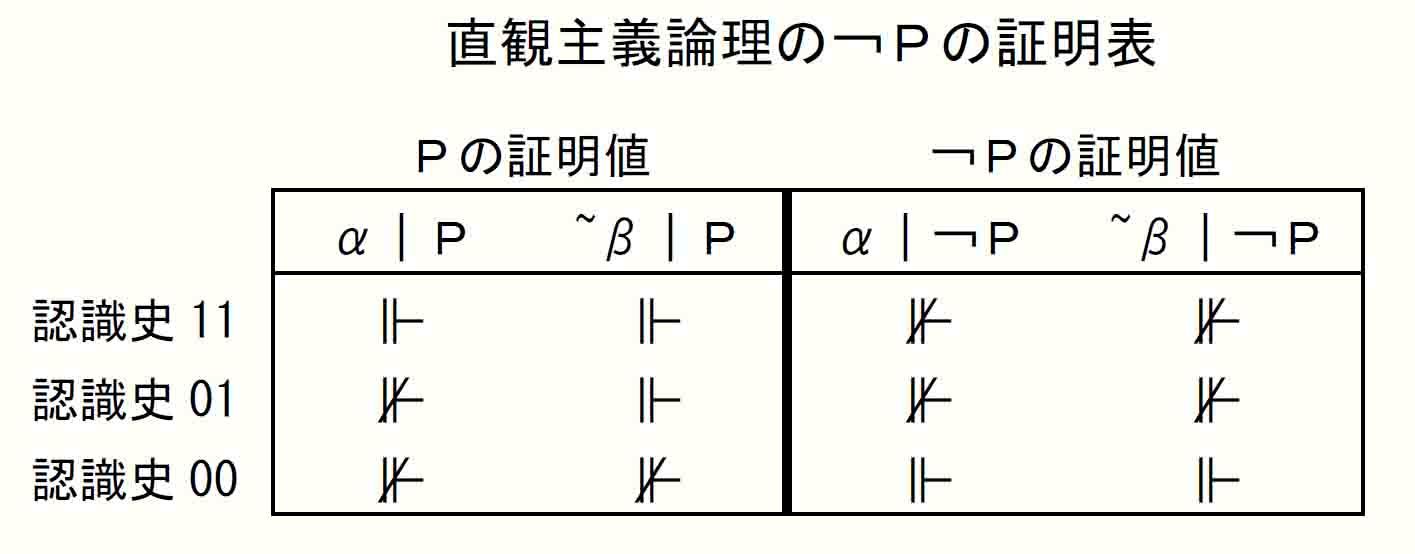
上の証明表からα期、~β期それぞれのPと¬Pの選言の証明値を直観主義論理の意味論規定Ⅱ(3)に従ってとってみる。
意味論Ⅱ(3) α⊩A∨B ⇔ α⊩Aまたはα⊩B
すなわち、Pか¬Pのいずれかが⊩のとき、P∨¬Pは⊩ということである。ここで意味論Ⅱ(3)のαとは「ある期」すなわち「同期」の意味であり、~βにおいても同様にこの規則が成り立つ。(Hard study 5-4-5 終わり参照)

直観主義論理のP∨¬Pの証明値が上表のようになることは、意味論規定からも直接、以下のように証明できる。
■直観主義論理P∨¬Pの証明値
認識史11α
認識史11によりα⊩P
ゆえに、α⊩P∨¬P
認識史01α
(前段 Hard study 5-2-3に既出)
認識史00α
意味論規定Ⅱ(3)←方向により、α⊩Pまたはα⊩¬Pならば、α⊩P∨¬P……(1)
もし(1)の前件が成立しなければ後件も成立せず、α⊮P∨¬Pとなる。
(1)の前件は選言なので「または」の前後いずれかが成立すれば、後件が成立する。
以下、α⊩¬Pであることを確認する。
意味論規定Ⅱ(5)←方向により、すべてのβで⊮Pならばαで⊩¬P
すなわち、α⊮Pかつ~β⊮Pの認識史のとき、αで⊩¬P
認識史00はα⊮Pかつ~β⊮Pなので、
αでは⊩¬P…(2)
(2)により、(1)の前件が成立することが確認された。
ゆえに(3)の後件が成立し、α⊩P∨¬P
認識史11~β
α⊩P∨¬Pなので~β⊩P∨¬P(式の証明は後続期に引き継がれる)
認識史01~β
認識史01では~β⊩P
ゆえに、~β⊩P∨¬P
認識史00~β
α⊩P∨¬Pなので~β⊩P∨¬P
続いて、¬¬Pの各認識史の証明値は以下の通り。
■直観主義論理¬¬Pの証明値
認識史11α
認識史11ではα⊩Pなので、α⊮¬P……(1)
また~β⊩Pであるから、~β⊮¬P……(2)
(1)、(2)と、Ⅱ(5)←方向により、α⊩¬¬P……(3)
認識史11~β
α⊩¬¬Pなので~β⊩¬¬P
認識史01α
認識史01では~β⊩Pなので、Ⅱ(5)←方向裏により、α⊮¬P……(1)
また~β⊩Pであるから、~β⊮¬P……(2)
(1)、(2)と、Ⅱ(5)←方向により、α⊩¬¬P……(3)
※このように、認識史01ではαで¬¬Pが証明されているのにPが証明されていない。この事態が二重否定除去則が公理ではないことを示している。
認識史01~β
α⊩¬¬Pなので~β⊩¬¬P
認識史00α
認識史00ではα⊮Pかつ~β⊮Pなので、Ⅱ(5)←方向によりα⊩¬P……(1)
(1)より~β⊩¬P……(2)
(2)とⅡ(5)←方向裏により、α⊮¬¬P……(3)
認識史00~β(2025年8月訂正)
¬Pの証明表を使う。
認識史00では~β⊩¬P。したがって、~β⊮¬¬P
以上から、直観主義論理の¬¬Pの証明表は次のようになる。
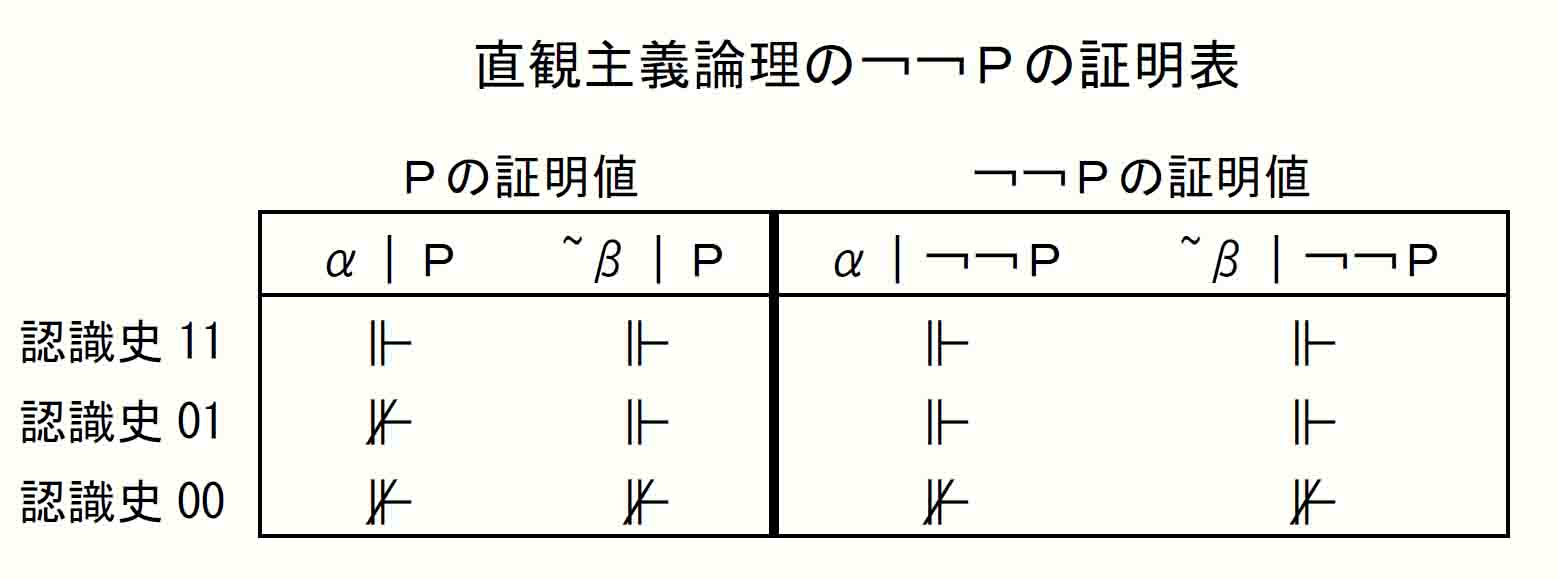
上の証明表からα期、~β期それぞれの¬¬PとPの証明値から条件法の定義(前件が真かつ後件が偽のとき偽)に基づいて¬¬P⊃Pの証明値をとると以下のようになる。(このやり方は直観主義論理の ⊃を定めている意味論Ⅱ(4)に基づくものではないので検証が必要。2021年2月記。→ 2024年2月、¬¬P⊃Pは、直観主義論理の ⊃の特異性(前件が偽のとき無条件に真とはならない。Hard study 5-5-1 )に触れない論理式のため、上の古典論理式の演算は方法として正しくないものの問題のないことを確認。)
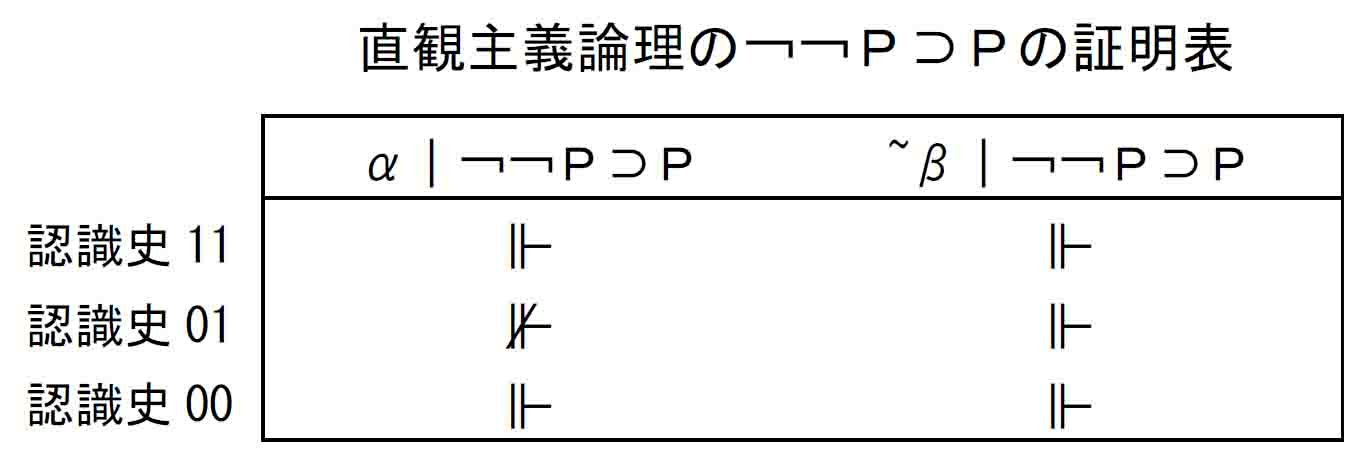
直観主義論理の¬¬P⊃Pの証明値が上表のようになることは、意味論規定から直接、以下のように証明できる。
■直観主義論理¬¬P⊃Pの証明値
認識史11α
認識史11ではα⊩Pなので、α⊮¬P……(1)
また~β⊩Pであるから、β⊮¬P……(2)
(1)、(2)と、Ⅱ(5)←方向により、α⊩¬¬P……(3)
前件が真、後件が真である条件式は真であるから、
(3)と、認識史11のα⊩Pにより、α⊩¬¬P⊃P
認識史11~β
α⊩¬¬P⊃Pなので、意味論Ⅲにより~β⊩¬¬P⊃P
認識史01α
(前節Hard study 5-2-3に既出)
認識史01~β
認識史01では~β⊩P
後件が真である条件式は、前件の真偽に関わらず真であるから、
~β⊩¬¬P⊃P
認識史00α(2025年8月訂正)
¬¬Pの証明表を使う。
認識史00では¬¬PおよびPの証明値は全ての期で⊮。したがって、¬¬P⊃Pにおいて前件は偽。
直観主義論理では、前件が偽であっても、前件が真かつ後件が偽である後続期が存在する場合は⊃式は偽となる。
しかし認識史00は全ての期で⊮¬¬Pなので、¬¬P⊃Pの前件が真となる期は存在しない。
したがって前件が偽である¬¬P⊃Pは真。すなわち、α⊩¬¬P⊃P
認識史00~β
α⊩¬¬P⊃Pなので、意味論Ⅲにより~β⊩¬¬P⊃P
ここでいま一度確認しておくと、知りたいのは意味論のどこに排中律および二重否定除去則の拒否が仕込まれているのかということ、そして意味論と構文論間の矛盾と見える事態をどう理解すべきかの二点である。
また(ロ)の意味を理解し、最終的には、Easy study 5-1からの問題意識である「古典論理と直観主義論理を分ける境界」について理解したい。
まず老婆心ながら次を確認しておく。証明表で確認してきた論理式を、今後、考察するにあたり、¬Pと¬¬Pではα⊮、~β⊩、P∨¬Pと¬¬P⊃Pではα⊮、~β⊮という証明状況が出ていないが、これで¬P、¬¬P、P∨¬P、¬¬P⊃Pにおけるすべての事態が言い尽くされているのかという疑問が起こるかもしれない。もしすべての事態が出ていないならば、上に導いた証明値に基づく今後の考察は不十分なものとなる懸念がある。
しかしこの懸念は、古典論理のトートロジーの真理表を思い出すことで払拭される。先に見た「P∨¬Pの真理表」や「前件肯定式の真理表」では当該列に1だけがあって0はない。それでもそれは排中律や前件肯定式のありえるすべての事態を示していたのであった。つまり、それらにおいては真理であることがありえる事態のすべてだったのである。論理式の考察において「ありえるすべての事態」というのは元の命題において求められることであって、演算を経た論理式で、真/偽、証明/不証明すべての組み合せが出揃うことを言うわけではないということである。
そのようなわけで、上の証明表からは早速次のことが明らかとなる。
¬Pと¬¬Pでは頭初期で不証明でありながら後に証明される事態というのはない。この事態は、命題Pに関しては認識史01として存在し、Pのあり方そのものだが、¬Pと¬¬Pではそれはないということである。
また、P∨¬Pと¬¬P⊃Pでは最終的に不証明に終わる事態がないことも帰結している。これが実際には何を言うものなのかは今のところまったく分からないが、次節でいくらかの理解が得られるはずである。