| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (14)
Hard study 5-3-1 「証明表」に見る直観主義論理の世界
さて、前節のP∨¬Pと¬¬P⊃Pの証明表からは、排中律、二重否定除去則ともに、認識史01のα期でのみ証明されない事態が起きていることがわかる。妥当式とならないのはこのためである。
したがって先に、道元言明とⅡ(5)(ロ)の整合性を図る解釈として挙げた、道元言明をα期のものとする見方は、ほぼ的を射たものであったといってよいだろう。認識史01α期でこれらが不証明となる理由をさらに探ってみよう。
排中律について先の証明(Hard study 5-2-3)をみると、認識史01α期でα⊮Pかつα⊮¬Pであるため、意味論規定Ⅱ(3)←方向が成立しないことが妥当式とならないことの直接の要因といえる。
ここで認識史01のα期でPが⊮であるのは当然だが、同じくα期で¬Pが⊮となることは、意味論規定Ⅱ(5)←方向(ハ)によって、αで¬Pが証明済であるためにはすべてのβでPが不証明でなければならないためである。認識史01では~β期でPが証明されるためこれが成立せずα期の¬Pは不証明となる。
そして同じことだが、αで¬Pが不証明となるのは、認識史01により~βでPが証明されており、この状況に対してⅡ(5)←方向裏(ニ)がαでの¬Pの不証明を与えていることによるともいえる。
つまり認識史01α期で排中律が成立しない要因となっているα期の¬Pの不証明は、後続期でPが証明されるという認識史01では当然である事態において、頭初期での¬Pの証明済が認められないというこれも当たり前である規則が原因となっているのである。いずれも当然のことであるので、排中律が妥当式とならない事情は理解できそうである。
すなわちα期で¬Pが未証明である事態というのは、直観主義論理の世界において当たり前だということである。したがって、これまでの証明表ではα期のPの証明値と、~β期のPの証明値の組み合せを出発点としていたが、α期のPとα期の¬Pの証明値の組み合せを出発点とする証明表を作成しても理解可能な証明表ができそうである。
そこで先に挙げた「直観主義論理の¬Pの証明表」の2列目と3列目を入れ替えてみる。
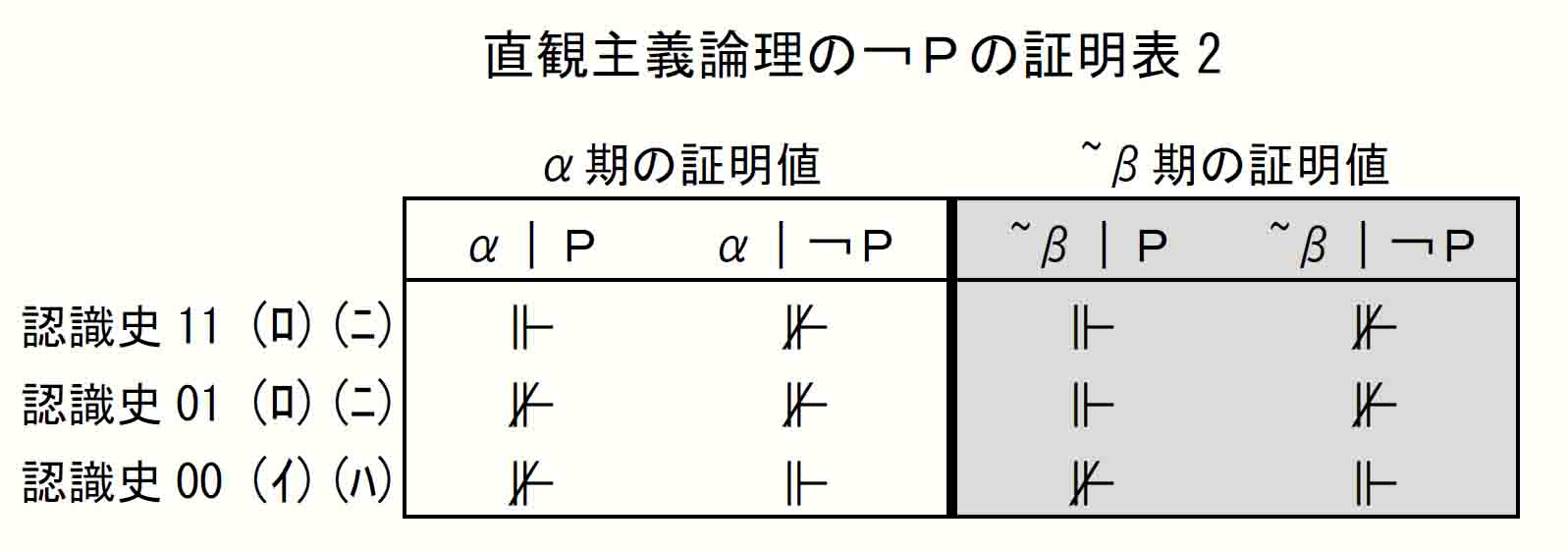
このようにすると意味論規定Ⅱ(5)(ロ)に該当する認識史01のα期に、Pも¬Pも未証明である事態が設定されることになる。しかもこの証明表には、α期においてP、¬Pの証明値のすべての組み合せが出ている。(α⊩P、α⊩¬Pという組み合せはないがそれは矛盾なのでなくてよい。)
ここには直観主義論理の世界観が明瞭に示されているといえるのではないだろうか。
つまり、古典論理の世界ではPのあり方だけから出発し、¬PはPによって真理値が決定される(Easy Study 2-2「¬Pの真理表」参照)。そこでは¬PはPに従属していた。
しかし直観主義論理の世界では、¬Pのあり方はPから独立しており、これら二つの命題の証明値の可能な組み合せが三通りあって、それを出発点とした世界が考えられているということである。
もちろん元の「直観主義論理の¬Pの証明表」の方を見れば、Pのαと~βの証明値のあり方が、¬Pのαと~βの証明値を決定しているのだが、それはα期におけるPと¬Pの関係を、古典論理のように証明値の反転として決定するものではなかったということである。
この頭初期におけるPと¬Pを、まず独立した関係に置いた上で、さらにその後続期でのそれぞれの真偽を問う真理観が、「証明/不証明」「構成/未構成」「観察できる/観察できない」などに解釈しうる直観主義論理の真理概念であり、命題と事実の一致/不一致による「真/偽」を真理概念とする古典論理とは異なる世界観を築くものなのである。(直観主義論理の基礎的な設定に関しては、Hard Studu 5-4-2 の「真理の余剰説」の箇所も参照のこと。)
上の考察により「排中律の拒否は意味論のどこに仕込まれているのか」という疑問は解決する。それは直観主義論理においてはPと¬Pを独立した関係にあるものとして設定しているところに仕込まれているのである。
Pが偽なら¬Pは真という固定した関係ではなく、Pが偽のとき¬Pが真(認識史00)でも偽(認識史01)でもありえるという関係が認められていることにより、排中律が常に成立するのではない世界となっている。
道元言明に即して言えば、無門が「¬Aが証明されえないならば残るはAじゃろ」と述べたのは認識史11のことであり、一方で、道元が「¬Aが証明されえないと分かったからといって、Aが証明されたわけじゃない」と述べることで、認識史01の存在が示唆されていたということが、上の「直観主義論理の¬Pの証明表2」から読み取れるのである。