| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (26)
Hard study 5-5-4 ハイティング代数とクリプキ意味論
頁内目次
(1) クリプキ系Ⅰ/Ⅱ型証明表とハイティング代数の複数モデル
(2) 束とブール代数
(3) ハイティング代数
(4) ハイティング代数の定義
(5) ハイティング代数の候補束
(6) → をどう定義すればよいか
(7) 定義第1式 (a∧x)≦b の意味
(8) 定義第2式 x≦c の意味
(9) 3値ハイティング代数表
(10) 3値ハイティング代数グラフ
(11) ガロア接続
(12) cが存在する束、存在しない束とは
(13) ¬の複数定義
(14) クリプキ系証明表とハイティング代数モデル、否定概念のまとめ
(1) クリプキ系Ⅰ/Ⅱ型証明表とハイティング代数の複数モデル <↓>
Hard study 5-2-4 の冒頭に記した宿題は、そこで作成してきた1命題証明表を2命題証明表に拡大し、直観主義論理の定理、非定理を確認することであった。
また、その結果を通じて、野矢茂樹『論理学』に書かれている「直観主義論理の意味論を真理表で表わすことはできない」というのが、どういう事態を指すものかを理解したいということである。
この目標に向けて直観主義論理の意味論の一つであるハイティング代数に取り組む中、WEB上のある記事に「直観主義論理におけるすべての定理/非定理を表現できるモデルは存在しない」という一文を見つけた。
直観主義論理の定理/非定理をもれなく表現するためには複数のハイティング代数モデルを要するということらしい。
詳細は不明であるものの、これにより先の宿題の答えは予想がつくものになった。すべての定理/非定理を表現するような単独のハイティング代数がないということであれば、すべての定理/非定理を表現できる単独のクリプキ系証明表もないだろうということである。
そもそも私がこの課題を負うことになったのは『論理学』の以下の記述による。
Hard study 5-2-4 に紹介した「分子式の分析」を一通り終えたところで、直観主義論理の論理的真理に関して次の会話が置かれている。(p.177)
無門「すると、さらに何が言えれば論理的真理になるのかね。」
野矢「こんなモデルをいくら作っても、必ずそのすべての知識状態で(その論理式に⊩が)成立していることが示されればいいわけです。」
道元「つまり、すべての可能な認識史のあらゆる時代の知識状態で成立している、ということか。」
無門「そりゃまたずいぶんきつい条件じゃな。」
野矢「でも、真理表のすべての行で1になるというのと同じですよ。」
「こんなモデルをいくら作っても」とあるが、ここで「こんなモデル」というのは「分子式の分析」を行ってきたところの認識史K0(認識史01)を指すことが明らかで、その上で「すべての可能な認識史のあらゆる時代で論理式が成立していることが、真理表のすべての行で1になるのと同じ」と言われている。
するとこのところからは、認識史K0以外の認識史についても「分子式の分析」を継続していって、すべての認識史のすべての期を証明値で埋めれば、その「証明表」(この呼び名は『論理学』では使われていないが)は式の妥当/非妥当を示すものとなるはず、という理解に導かれる。それ以外には理解のしようがない。
「直観主義論理の意味論を真理表で表わすことはできない」と書かれていたのが、これに先立つわずか数頁前のことであって、したがって、「分子式の分析」によってできあがるであろう「証明表」という考えはその記述とつじつまが合わないと感じるのだが、「分子式の分析」の遂行によって「証明表」ができあがることはあまりにも明らかなことであるので、数頁前の「真理表(証明表)はできない」という記述を鵜呑みにすることの方がはるかに困難と感じられるのである。(ここで「鵜呑み」と言わなければならないのは、この記述に関係する説明が一切ないからである。)
そこで、Hard study 5-2-4で作成済みの1命題2期3行の¬の証明表に加えて、2命題4期9行からなるⅠ型基本証明表(∧、∨、⊃)を作成し、それを用いて12個の論理式を調べてみたわけだが、その結果2個について、Hard study 5-5-1に既述の通りⅠ型証明表はそれを正しく表示しないことが判明した。
上の『論理学』の会話から予想されるところからは、この状況は理解しがたいものである。Ⅰ型証明表はすべての認識史のすべての期の証明値、すなわち「道元」の言う「可能な認識史のあらゆる時代の知識状態」を明らかにしたものだからである。しかしとりあえず、そのうまくいっていない2個の解決のために、まずⅡ型証明表、そしてⅠα型証明表を作成した。
このとき私は『論理学』から得た見通しに立ち続けたままなので、当然ながら、Ⅰα型証明表とⅡ型証明表を作成する根拠のようなものは見えていない。本来は、Ⅰ型証明表によって直観主義論理のすべての定理/非定理をきちんと表示できるはずだが、それができないということはこの証明表に何かしらの欠陥があり、それを解決する別の証明表を作成することで、その欠陥が見えてくるかもしれないといった見通しを持つだけだったのである。
全く新たに考案したⅡ型証明表については、当初、それがド・モルガン律(2)aを正しく表示することから、すべての論理式に使えるという期待を抱いたが、「プレ線型性」を正しく表示しないことが明らかになった時点で公表に価しないと判断した。このためさらに「プレ線型性」のためにⅠα型証明表を考案しなければならなかったのだが、Ⅱ型証明表についてはやはりド・モルガン律のためのアドホックなものにすぎないと判断したのである。(もっともⅠα型証明表はⅠ型証明表と同等であり、Ⅱ型証明表はⅠ型証明表の上位互換なので、「プレ線型性」を読みとるためのⅡα型証明表を作ることは容易だったのだが。)
この結果を受けて、私は自らに課した宿題について「どうまとめたものか」という望まない思案に陥ることになった。
「直観主義論理におけるすべての定理/非定理を表現できるモデルは存在しない」という先の一文を目にしたのはその折りである。そこで私の「目の梁」は取り除かれた。そういうことであれば俄然状況は変わる。Ⅰ型証明表が12個の論理式全部を正しく表示しないのは当然のこととなり、Ⅱ型証明表はⅠ型を補完する証明表として機能している可能性が考えられてくるのである。
つまり「道元」の言う「可能な認識史のあらゆる時代の知識状態」とは、「一つの証明表の中の知識状態」の話なのではなく、別種の「証明表」や、あるいは「証明表」のような二次元マトリクスで表現できるものとも限らない、とにかく可能である限りのすべての知識状態を言うものであったというのが真相だったということである。(もっとも『論理学』の中ではとてもそのようには――つまり「真理表で表すことはできない」というのが「一つの真理表だけでは表せない」という意味だとは――読めないのだが。)
そこでⅡ型証明表は複数のハイティング代数モデルが果たす役割と同じ役割を果たすものとまでは言えないが、この証明表で何がなされようとしたかについての全体的な視点に立った見方が可能になった。
見るところでは、Ⅰ型証明表の行数と証明値は、{0, ½, 1} の3値からなる最も簡素な(とはいえ難しいが)ハイティング代数の真理表と全く同じであり、また、{0, ⅓, ⅓', ⅔, 1} の5値からなるハイティング代数はいくつかの点でⅡ型証明表と似ている。
というのは、5値ハイティング代数モデルはⅡ型証明表と同じく、ド・モルガン律(2)aの非定理性を示すために使われているからである。ド・モルガン律(2)aは、Ⅰ型証明表と同じく、3値ハイティング代数では非定理性を示せないらしい。また、後述のとおり、5値ハイティング代数はⅡ型証明表と同様に、3種類の偽を定義していると見える。
このHard study 最終節では、これまで見てきたクリプキ意味論とは異なるアプローチを持つハイティング代数によって、直観主義論理意味論を改めて学んでみたい。(なお、Ⅱ型証明表については2025年8月に再判断してWEB掲載を取り止めた。)
ハイティング代数はクリプキ意味論と並ぶ、直観主義論理のもう一つの意味論である。
古典論理の意味論は、論理記号(¬、∧、∨、⊃)で結ばれる分子命題の真偽を、原子命題の真偽のあり方に応じて0か1を与える真理表によって表現されていた(Easy study 5-2-1冒頭)。この古典論理の真理値の集合{0,1}は「ブール代数」と呼ばれる。
直観主義論理の真理値の集合は「ハイティング代数」と呼ばれ、ブール代数が古典論理の意味論すなわち真理表を形成するのと同様に、ハイティング代数は直観主義論理の意味論となる。
このハイティング代数が、これまでに見てきた論理式を含め、非定理のド・モルガン律とプレ線型性式をどのように表現するのか、その非定理性を示すことができるのかを確認したい。
ハイティング代数を学ぶにあたり、まず、より理解しやすいブール代数から見ていくことにする。
さて、代数というのは数字を文字で置き換えて演算規則などを考える「代数学」で使われる文字や数字のことで、ブール代数としては{0,1}の他にも、有限集合のべき集合などがある。
べき集合とは集合の部分集合全部を集めた集合のことで、例えば、集合{a,b}のべき集合は{{ab},{a},{b},{φ}}(φファイ=空集合)であるが、これも後に述べるブール代数の要件を満たす集合となっている。(以下、べき集合の要素では集合記号 { } を省略する。)
代数は演算が可能であり、ブール代数{0,1}の演算が、古典論理の真理表に対応するものであることが下の真理表から確認できる。
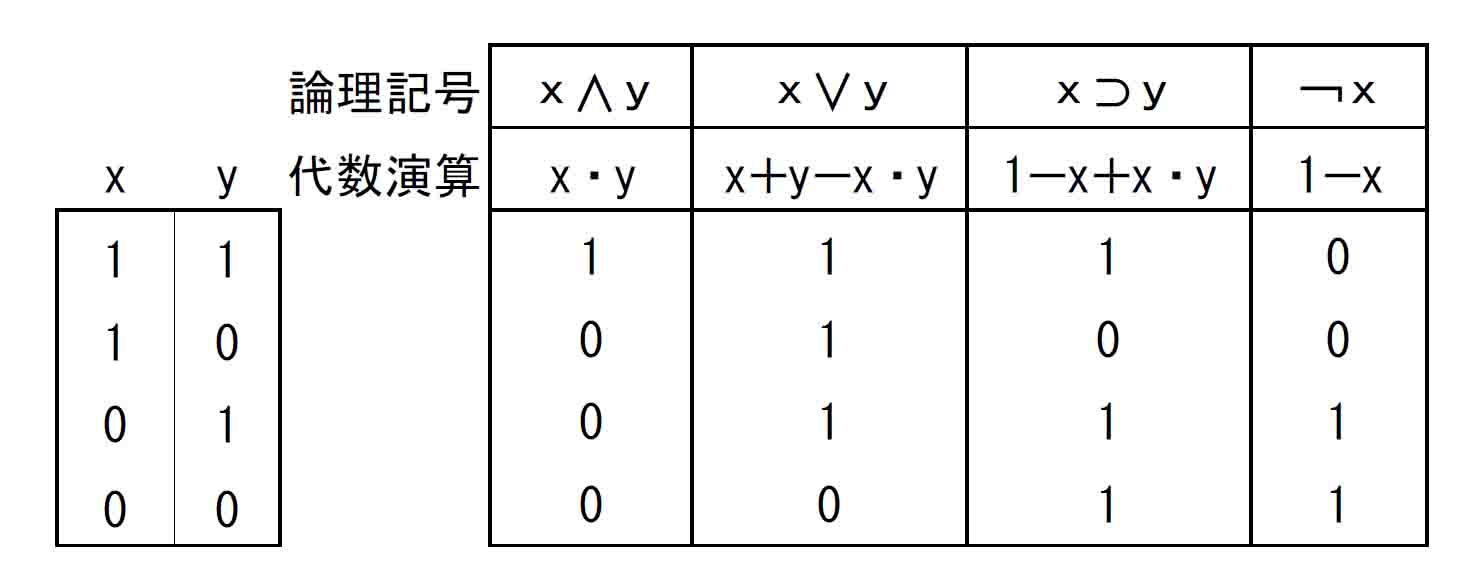
真理表の0、1について、先の箇所(Easy study 5-2-1)では真理表の中では未定義であると述べた。真理値0、1は、哲学的な「真理の対応説(Easy study 1)」による意味付けを持つものとして理解されるからである。
例えば、二つの命題X、Yがあるとき、「『XかつY』は真」という言い方ができるのは、XとYが共に真であるときだけで、事態がそれ以外の場合には「『XかつY』は偽」とする。これが上の真理表のx∧y列の1行目から4行目の真理値1000に表現されていることである。
代数演算では分子命題の真理値を、原子命題X、Yの真理値を用いた計算によって求める。Easy Study 2-2で見た真理値分析では、基本の真理表を使いながら、分子命題の真理値を一つ一つ手計算していたが、ブール代数演算を使えばこれを機械化できるということである。
ただしこの演算式はいくらか難しいので、特に∨や⊃の計算がどうしてこの式になるのかを理解するには若干の労力を要する。その労力はわずかだが、ここで理解したい内容からは離れるので解説が載っている書籍の紹介にとどめる。
このブール代数演算は、論理記号が持つ「真理の対応説」的意味を工夫して計算式にしたものであって、真理値の定義という観点からは「真理の対応説」以上の意味を持つものではない。言いかえれば、論理計算の機械化に役立つこの演算は、少なくとも真理表を扱ってきた者に対しては真理値0、1に関する理解を深めるものではない。
一方、以下に見ようとするブール代数とハイティング代数についての定義は「真理の対応説」とは別の観点から行われていて、真理値0、1について新たな理解をもたらす。
ブール代数、ハイティング代数は「代数」と呼ばれることから、数字や英文字による演算の値としてのイメージがあるが、実は集合のことである。これらの「代数」は、集合のある特質として定義される。
これらの代数は「順序集合」という集合を出発点として定義される。(なお「順序集合」には「半順序集合」「部分順序集合」という別の呼び名もある。)
順序集合というのは、数字や文字列や集合を要素とする集合において、要素間に大小や含有、前後などの関係による序列がつけられた集合のことである。
例えば、集合{0,1}は≦(大小)によって順序付けられ、集合{a, b}のべき集合{ab, a, b, φ}は⊆(含有)によって順序付けられた順序集合である。
順序集合のうち、集合内の任意の2つの元が共通の「上界」を持ち、その共通の上界に「最小元」があるとき、これを2つの元の「上限」とする、という決まりがある。
数学用語が続出したがここは難しくない。「上界」というのはその元を含むそれよりも大きな元全部のことで、例えば、順序集合{0,1,2,3}において、1の上界は{1,2,3}、2の上界は{2,3}である。そこで、1と2の共通上界は{2,3}であり、この中の「最小元」2が、1と2の「上限」ということになる。
同様に、集合内の任意の2元が共通の「下界」を持ち、その共通下界に「最大元」があるとき、これをその2つの元の「下限」という。
順序集合{0,1,2,3}において、0の下界は0を含めたそれ以下の元のことなので{0}、2の下界は{0,1,2}である。そこで、0と2の共通下界は{0}であり、その「最大元」0が0と2の「下限」ということになる。
任意の2元に関してこの「上限」と「下限」が存在する順序集合を「束(そく)」という。つまり順序集合{0,1,2,3}は束であり、この束にさらにある規則が加わったものがブール代数となる、という流れである。
理解をなじませるために、束と束ではない順序集合について見ておくと、まず、集合{a, b}のべき集合{ab, a, b, φ}は束である。
この場合、4個の要素は{ab}を頂点とする◇型のような、途中で枝分かれする形に配置され、横に張り出したところに{a},{b}が位置し、下端に{φ}(空集合ファイ)がくる。
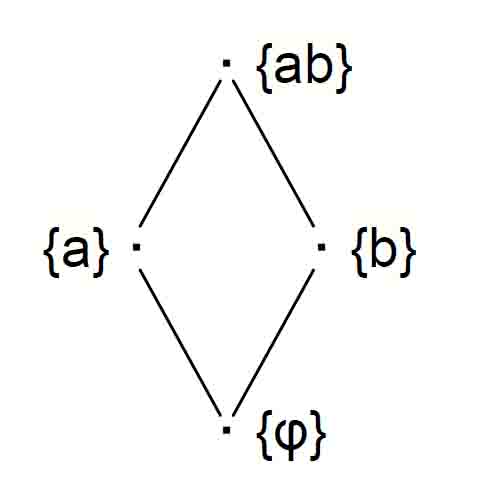
したがって {a}, {b} 間には順序関係はつかないが、それらの共通上界は{ab}であり、また{ab}自身が共通上界の最小元なので{a}, {b}の上限は{ab}として存在する。また、共通下界は{φ}で、それ自身共通下界の最大元でありこれが下限である。このようにして、{a} と {b} 以外の組においても上限と下限が定まるので、これが束であることが確認できる。
束ではない順序集合というのは、例えば、4個の元からなる集合{a, b, c, d}が、Yの字に配置される場合(a, b がYの2本の枝それぞれの上端、c がYの中心、d がYの下端)、上端のa, b を組とするとこの2元には共通の上界が存在しないので(aの上界はa、bの上界はb)上限が定まらず、これは順序集合ではあるが束ではない。(下限についてはどの2元を取ってもcまたはdに定まるので、このような場合の順序集合は「下半束」と呼ばれる。)

なるほど形から見ても◇は束(たば)だがYは束(たば)ではないといえる。
順序集合{0,1,2,3}のようにI型に1列に配置される順序集合は、◇型の{a}, {b}のように順序関係を持たない元の組がないため「全順序集合」と呼ばれる。そしてこの場合、「上限」「下限」は、上に述べた「共通上界の最小元」「共通下界の最大元」という面倒な言い方をしなくてもすむようになる。

I型順序集合における「上限」は、2元のうちの「大きい方」と言えばよい。下限も同様、2元のうちの「小さい方」ということで誤りなく指定できる。このため、古典論理の真理値の集合{0,1}が考えられているときは、これは全順序集合であるから、上限は2元のうちの大きい方、下限は小さい方という理解で賄うことができる。
このように順序集合に対して「上限」と「下限」という概念を加え、これを満たす順序集合が、言いかえれば「上限」と「下限」が存在する順序集合が「束」である。
そしてこのとき、上限を求める操作、下限を求める操作は、それぞれ2元に対する計算であるということができ、上限を求める計算を∨演算、下限を求める演算を∧演算とみなすことができる。この点を真理表から確認してみる。
これまでの理解では、∧と∨の真理値は「真理の対応説」に基づくあり方として得られる真理値であった。∧式はxとyの「かつ言明」成り立つとき真とするのが適切であり、∨式はxとyの「または言明」成り立つとき真とするのが適切であるという見通しから、∧と∨の真理値が定められていたのである。
厳密にはEasy Study 2-2で述べた通り、「論理記号の意味に合うように1と0を配置しているのではなく、1、0をそう配置することによって論理記号の意味を定めている」のであり、この点は⊃(条件法)と≡(同値)の区別や、∨(両立的選言)と▽(排反的選言)の区別においては特に重視されなければならないことであった。
そもそも論理学とはただ「真理の整合説」にのみ依拠する体系であり、「現実との対応」つまり「意味内容」から独立したものだが、構文論において整合説を完全に満たす体系を整えた上で、その体系と現実との対応を見ようとするものでもある。それが意味論の役目である。
しかし束論のこの段階ではこういった「かつ」や「または」の意味による理解は一切考えない。単純に、x、yの真理値と、∧、∨の真理値を比較してみると次のことに気がつく。
すなわち、∧の真理値というのはxとyの真理値のうち小さい方を採用したものであり、∨の真理値はxとyの真理値のうち大きい方を採用したものだということである。
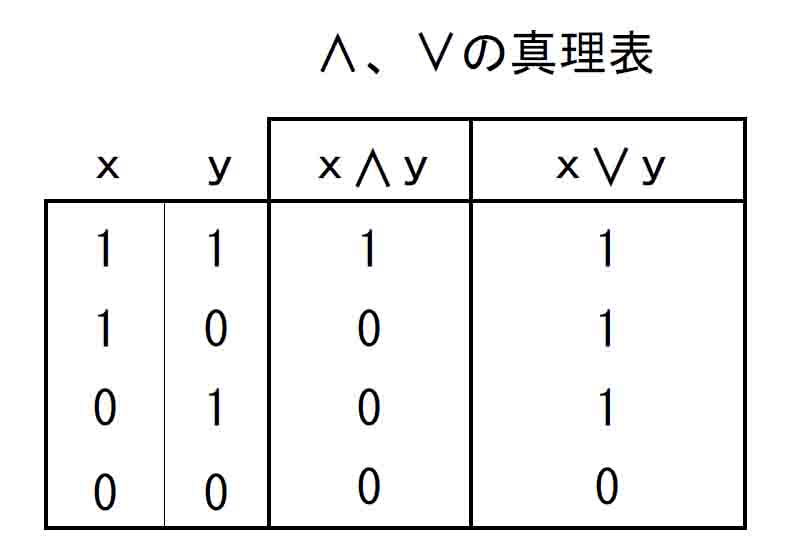
つまり∧というのは2元の下限を求める演算であり、∨は上限を求める演算であったということである。
上限、下限の考えでいくと、1と1の下限は1で、上限も1である。これが上の真理表の1行目のx∧y列と、x∨y列の値となっている。
同様に1と0の下限は0、上限は1で、これが2行目の∧列と∨列の値であり、3行目も同様である。4行目は、0と0の下限は0、上限は0、これが∧列と∨列の値である。
なお、順序集合{0,1}において1と1、0と0のように、同じ元を2つ考えることについて疑問が起こるかもしれないが、この点は順序集合の定義に、「反射律」(x≦x)、「非対象律」(x≦y、y≦xならばx=y)という規則が含まれていることから説明される。反射律は、0や1についてもう一つ同じ元を考えてよいことを示すものといえる。これに「推移律」(x≦y、y≦zならばx≦z)を加えたものが、集合が順序集合であるための条件となっている。
そこで繰り返しの確認となるが、「順序集合」に∧演算と∨演算が加わったもの、すなわち任意の2元ついて「上限」と「下限」が存在しているのが「束」である。
ブール代数はこの「束」に「補元」という元が加わったものである。プール代数一般を考えるときには「補元」の他に、その束において分配律が成り立つ「分配束」という性質が必要になるが、ここではブール代数として束{0,1}だけを考えるので「分配束」については省略し、この束{0,1}が「補元」を持つものであるかを確認したい。
なお、束{0,1}が分配法則を満たす束であることは、0と1をあてがった8通りのx,y,zの組み合わせの全てにおいて、x∧(y∨z)=(x∧y)∨(x∧z)が成り立つことを見ることで確認できる。(ここでは省略する。)
さて、「補元」とは、束{0,1}の任意の元xについて、次の性質を同時に満たす元yのことで、意味としてはxの「否定」に相当する。
x∧y=0
x∨y=1
束{0,1}で考えると、xを0とすると、
0∧y=0
0∨y=1
となるようなyのことである。ここでyに1を与えると
0∧1=0(0と1の小さい方は0)
0∨1=1(0と1の大きい方は1)
であるから、1が0の補元であることが分かる。
そしてこの1は、言うまでもなく束{0,1}の元として存在するものである。
同様にxを束{0,1}の1とした場合は、
1∧y=0
1∨y=1
となるyは0である。すなわち、
1∧0=0(1と0の小さい方は0)
1∨0=1(1と0の大きい方は1)
であるから、0が1の補元となっている。
そして、この補元0は束{0,1}の元として存在している。
つまり束{0,1}においては、2元の双方が、互いの補元となっているということである。
そこで、このような性質を持つxの補元yを¬xと書く。すると、
x∧¬x=0 (矛盾律)「xかつ¬xである」ことはない
x∨¬x=1 (排中律)「xまたは¬x」という言明は常に真
という見慣れた論理式となる。
論理記号∧、∨が2項目演算であるのに対し、¬は1項目演算でありxの値が決まることで¬xの値が定まることになる。先の「分配束」という条件は、このときxの補元が一意に定まること、すなわち補元を¬という写像として表現できるための条件である。これについての証明は[注]資料参照。
以上をまとめると、束とは上限と下限が存在する順序集合のことで、ブール代数とはxに対する¬xが定義できる束のことである、ということである。
なお、先にブール代数の要件を満たすと書いた、集合{a,b}のべき集合{ab, a, b, φ}について、その補元を確認しておくと次のようである。
集合を元とするブール代数の補元¬xは、xの差集合として定義される。したがってxが{a}のとき、¬xは{ab, b, φ}である。
これが補元の性質を満たすことは次のように確かめられる。
順序関係が⊆である集合、つまり元が集合である集合の場合は、∧演算は集合の∩(共通集合)を求める演算であり、∨演算は集合の∪(和集合)を求める演算である。
x∧¬x:=x∩¬x={a}∩{ab, b, φ}=φ(空集合なので0相当)
x∨¬x:=x∪¬x={a}∪{ab, b, φ}={ab, a, b, φ}(全体集合なので1相当)
(:=は「定義」の意味)
ハイティング代数はブール代数よりも規則が緩い束である。古典論理の二重否定除去則を、より緩い否定除去に置き換えた直観主義論理(Hard study 5-3-2 注[5])が難しいのと同じく、規則の緩いハイティング代数はブール代数よりも理解が難しい。
見てきたように、古典論理におけるブール代数は、順序集合に∧と∨を定義して束となったものに、補元による¬演算を加えたもので、古典論理の⊃は、この∧と¬を使って定義される。そしてこれが先に見たブール代数⊃演算の1-x+x・yという式にもなっている。
また、補元¬xの存在によりブール代数は「x∨¬xは常に真」という排中律が成立する代数になっている。 そこで、ハイティング代数がどういうものかを考える際には、ここまで直観主義論理が排中律を定理として持たないことを見てきたので、補元を定義できない束としてそれを考えることが我々にとっての近道となる。
このとき補元すなわち¬が定義できないということは、∧と¬を使った →(⊃のハイティング代数版)の定義ができないことを意味する。そのためハイティング代数では → の定義を独自に行うことになる。
補元による¬の定義に代えて、先に → を定義し、その後、この → を使って¬を定義しようというのがハイティング代数である。
したがって、独自に定義される直観主義論理の → は古典論理の⊃とは働きが違っており、その結果、この → を使って定義される直観主義論理の¬も古典論理の¬とは働きが違うものになる。
なお、→ 記号は、これまでの説明に用いていた⊃記号と同じ条件法の結合子だが、束論では → が多く使われているようなので、以下、ハイティング代数では → を使うこととする。以下に限り、⊃は古典論理の条件法、→ は直観主義論理の条件法を示すものと理解されたい。(これまでの記述では直観主義論理でも⊃記号を使ってきた。)
代数学の書籍やWEB文献に紹介されているハイティング代数の代表的な定義は以下である。
定義式①
束の任意の元 a, b, c, x があるとき、これらが
(a∧x)≦b ←→ x≦c (←→は双条件)
であるような元cが存在する束をハイティング代数と呼び、このcをa→bとする。
Easy study 5-2-1で見たクリプキ意味論は、初め何を言っているのか見当がつかないものだったがハイティング代数も同様である。上の定義に大まかな概念図が添えられていることがあるが、それが助けになるという人はまずいないだろう。
後ほど見る「ガロア接続」という写像概念を理解することで、その往復写像の図から上の定義をいくらかイメージできるようになる。しかしそこから明瞭な理解に至るためには「随伴」などの深遠な概念を知る必要があり、かなり遠回りしなければならない。
そこでここでは、理解しやすいと私が考える順序で、また言わずもがなであるが、私が理解している範囲でハイティング代数を説明していくことにする。
上の定義はひとまず置いておき、ハイティング代数が、排中律が成立しない直観主義論理の意味論を形成する代数であり補元のない束である、ということを出発点としよう。
正確に言えば、補元を持つブール代数はハイティング代数の特殊な場合であり、ハイティング代数の一種であるので、ハイティング代数に補元がある場合もあるというべきだが、ここではハイティング代数からブール代数を除いて考えることで、ハイティング代数独自の形式を捉えたい。
そこでとりあえず補元がない束というものを考えてみる。
束{0,1}に元½を加えた3値からなる全順序集合の束{0, ½, 1}はどうか。
0と1に関しては互いが補元となることを見てきたので、新たに加えた元½に補元となる元があるかを確認してみる。
補元は束の中に見い出されなければならないものなので、補元候補は0、½、1の3つである。
繰り返しになるが、補元とは、
x∧y=0
x∨y=1
を同時に満たすyのことである。
そこでxを½とした上で、yに3つの候補値を代入して確かめてみる。
y=0 としたとき、
x∧y=½∧0=0
x∨y=½∨0=½
y=½ としたとき、
x∧y=½∧½=½
x∨y=½∨½=½
y=1 としたとき、
x∧y=½∧1=½
x∨y=½∨1=1
である。
したがってyがいずれであっても、上の補元の定義式は満たされない。
つまり束{0, ½, 1}は、任意の元において補元が存在するのではない束であり、ハイティング代数となる資格があるといえる。
次に、このハイティング代数の候補束{0, ½, 1}、つまり補元のない束に、補元(¬)に頼らずに → を定義することを考える。
ブール代数の箇所で見た通り、束においてはすでに∧と∨が定義されている。これに → を定義することでハイティング代数になるのである。
このとき参考にするのは当然のことながらブール代数の⊃である。というのは、→ をできるだけ⊃のように定義できれば、それは「うまく定義した」こととなって、この新たな代数においても、→ を古典論理の条件法に準じた扱いができるようになるからである。
Easy Study 2-1 の「A⊃Bの真理表」を再掲して、古典論理の⊃の働きを確認してみる。
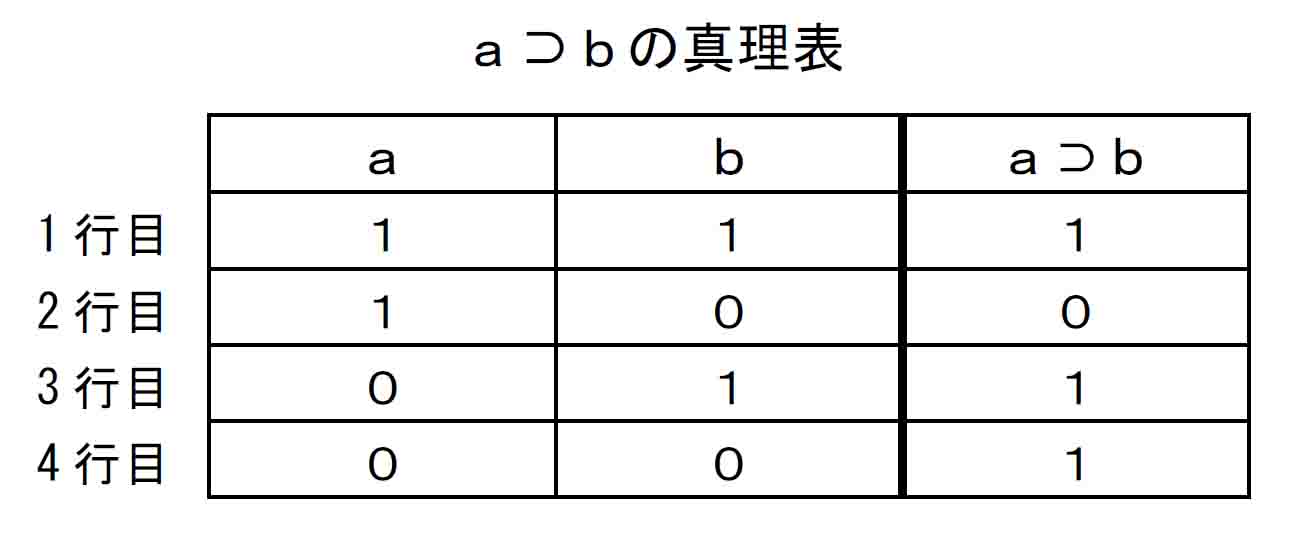
古典論理ではa⊃bの真理値を、その対応説的意味から考えて、前件が真であるのに後件が偽であるときに偽、それ以外は真であるとした(Easy Study 2-1)。
しかしここでは、a⊃bの定義をaとbの大小関係に注目して捉えてみる。それは、順序集合から束に至る過程での∧と∨の導入が、やはり2つの元の大小関係の演算として定義されたことに倣うということである。
そこで⊃について同じようにやってみる。するとa⊃bの真理表からは、次の規則を見いだすことができる。
a≦bのとき、a⊃b=1(1、3、4行目)
a>bのとき、a⊃b=b(2行目)
a>bの場合はa⊃b=0として捉えることもできるが、a>bである行は1行しかないので規則の汎用性を考えて、特定の真理値ではなくbの値としておきたい。
この規則に従って、束{0, ½, 1}でのa→bの真理表を作ってみる。3値2命題真理表なので、3^2=9行の真理表となる。
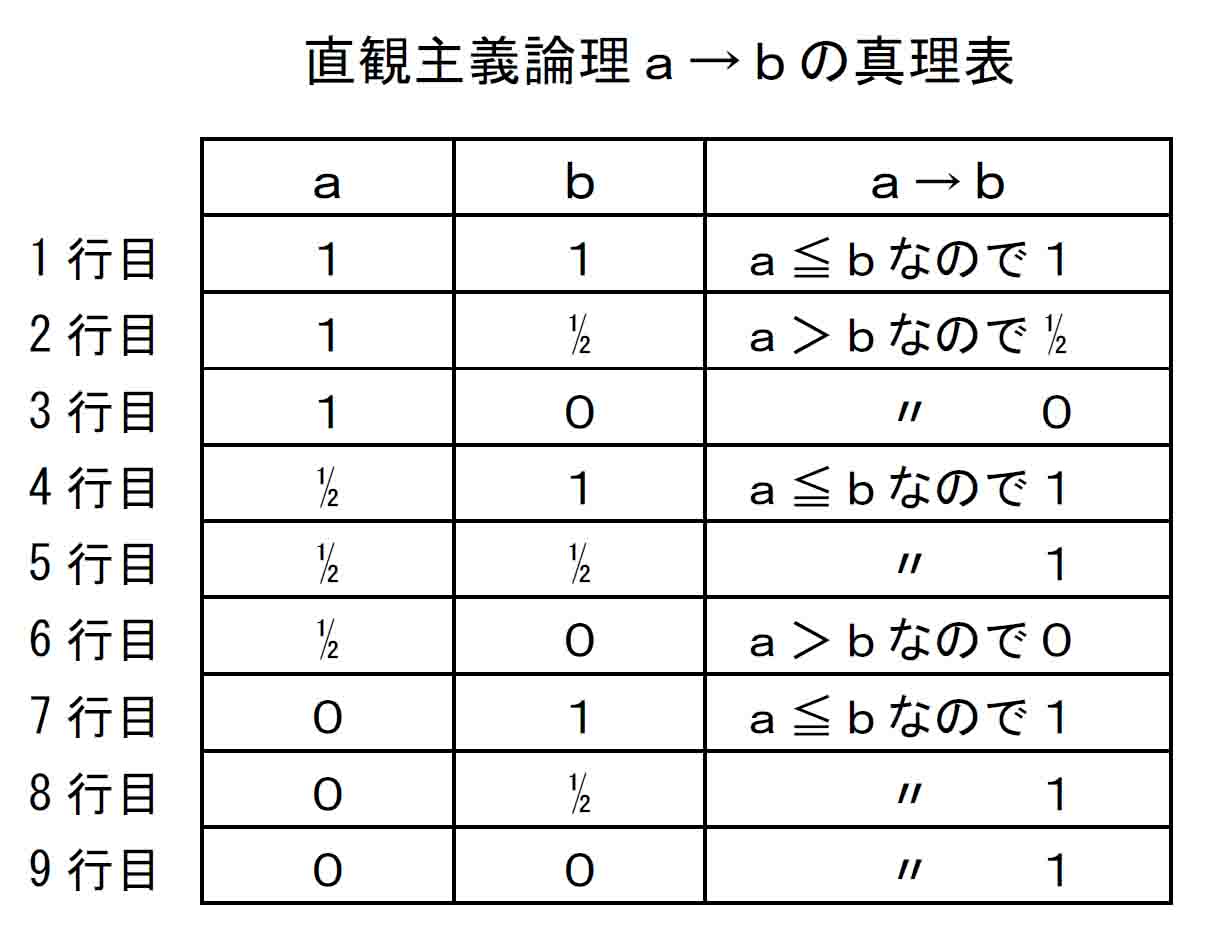
とりあえずa→bの真理値が出た。
このa→bの真理値が → に求められている働きをきちんと果たしているかを知るにはどうすればよいだろうか。 古典論理の⊃の働きを如実に表現するものとして前件肯定式がある。(Easy Study 2-2 より)
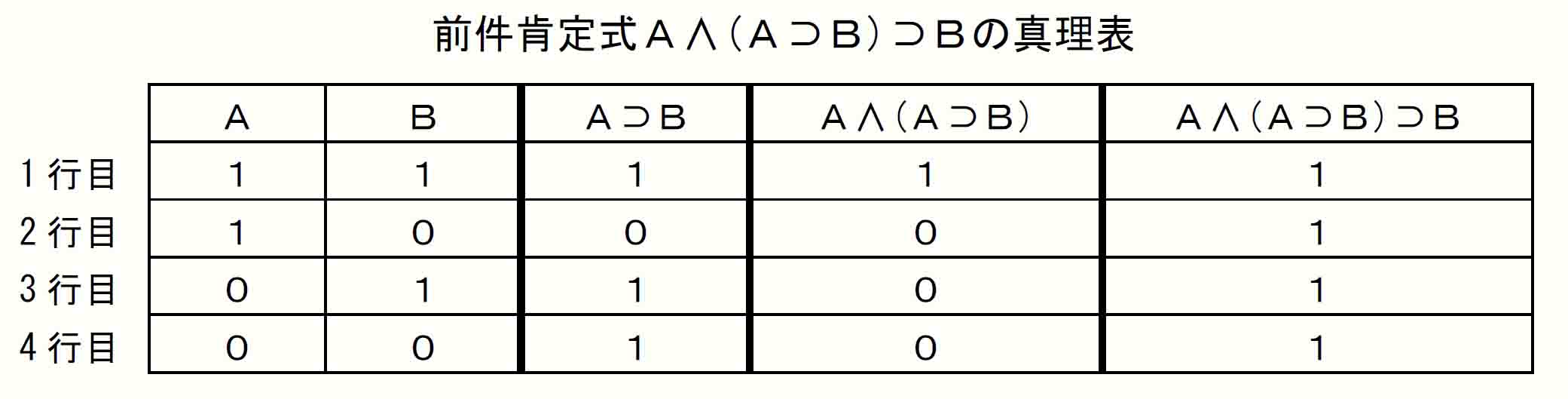
すなわち a∧(a⊃b)⊃b である。
この前件肯定式(MP=Modus Ponens)は、古典論理における規則、定理であるにとどまらず、論理体系の無矛盾性や健全性などを、その論理体系の外からメタ論理として検証する際にも使用される最も基礎的な論理式である。
上に作成した「直観主義論理a→bの真理表」において、このMPが成立していれば、a、bの大小関係から導いた「a→b」における「→」は「うまく定義されている」ということになるだろう。
そこで「a→bの真理表」から前件肯定式の左辺a∧(a→b)を計算して、それをbの値と比較してみる。(∧演算の値は両辺の小さい方)
ここで、全行で前件肯定式a∧(a→b) → bが成立しているのは当然である。前件肯定式はa∧(a→b)の値が、bと等しいか小さいことで成立するが、上表はこの性質をa⊃bの真理表からくみ取ってできあがったものだからである。
確認すると、a≦b(1、4、5、7、8、9行目)の場合、a→bの値は最大値である1としたが、aはbより小さいので、たとえa→bがどんな値であったとしてもa∧(a→b)はbより小さいことになる。したがって前件肯定式が成り立つ。(分かりにくい人のために別の言い回しをすると、ここではa→bの値は1なので、a∧(a→b)=a∧1=a。いまa≦bであるから、a∧(a→b)≦b。)
a>bの場合(2、3、6行目)、aはbより大きいが、a→bをbの値としているので、aがどんな値であったとしてもa∧(a→b)はbの値を超えることはない。したがって前件肯定式が成り立つ。(同じく別の言い回しをすると、ここではa→bの値はbなので、a∧(a→b)=a∧b。いまa>bなのでa∧b=b。したがってa∧(a→b)=b。)
このように上表全行でMPが成立することは当然のことにすぎないので、これをもってa→bを古典論理のa⊃bと同じように設定できたと見なすことは早計である。MPの性質をさらに詳しく見てみなければならない。
そこで先の「前件肯定式A∧(A⊃B)⊃Bの真理表」を見直して、a∧(a⊃b)とbの真理値関係から、MPで何が実現されているかを、もう一度捉え直してみる。特にaの真偽に注目するのは、aはここで条件法の前件であり連言の単独要素でもあることから、いずれも式全体の真理値を決定づける役割をしているためである。
1行目 a=1で、a∧(a⊃b)=1、b=1のとき、a⊃bは1である。
このとき、a∧(a⊃b)=bが成立している。
2行目 a=1で、a∧(a⊃b)=0、b=0のとき、a⊃bは0である。
このとき、a∧(a⊃b)=bが成立している。
3行目、4行目 a=0のときは、a∧(a⊃b)とbの真理値は一致したりしなかったりする。つまりa=0のときはa∧(a⊃b)=bは成立しなくてよい。
前件肯定式の真理表ではa∧(a⊃b)⊃bだけではなく、aが真の場合にa∧(a⊃b)=bが成立している点が注目される。このことから、直観主義論理において実現されるべきa→bを考えると、
1行目の考察から
① a∧(a→b)=1で、b=1のとき、a→bは1であってほしい。
そしてこのときa∧(a⊃b)とbは同値であるべきである。
2行目の考察から
② a∧(a→b)=0で、b=0のとき、a→bは0であってほしい。
そしてこのときa∧(a⊃b)とbは同値であるべきである。
3、4行目の考察から
③ a=0のときは、a∧(a⊃b)とbの値は一致していなくてよい
ということになる。
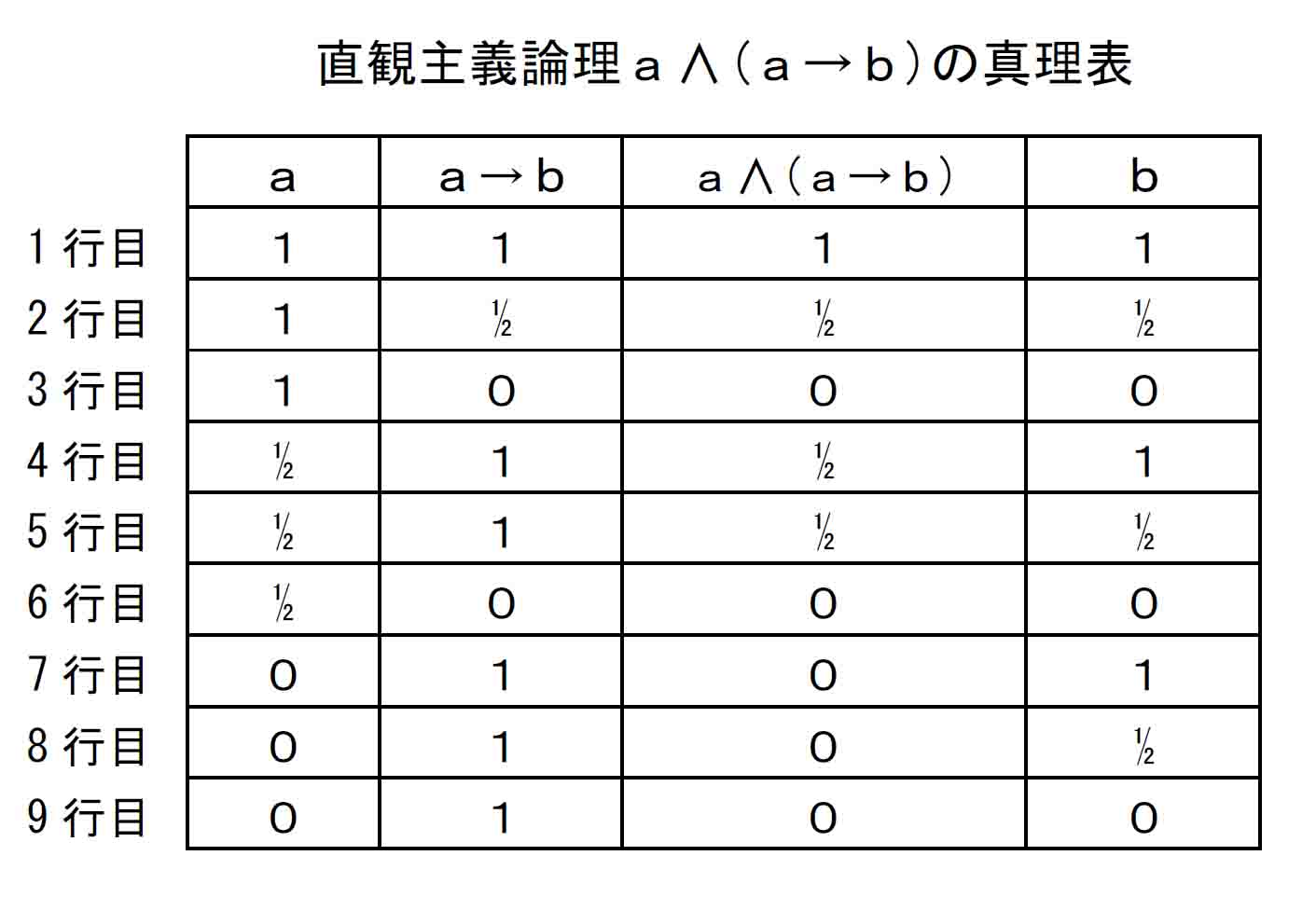
a→bに関する上の要請が、先のa∧(a→b)の真理表で実現されているのかを確認してみる。a∧(a→b)の真理表を再掲する。
①については、1行目がこれを満たしているので、①の印をつける。
②については、3行目と6行目がこれを満たしているので②の印をつける。
③については、7行目、8行目、9行目が該当しているので③の印をつける。

印がつかなかった残り3行についてはどうか。
2行目はa∧(a→b)=½ 、b=½ で、a→bは½である。
5行目はa∧(a→b)=½ 、b=½ で、a→bは1である。
いずれも①の前半の要件は満たしていないが、しかしa∧(a⊃b)=bという前件肯定式において必須である後半の要件は満たしている。
したがって2行目と5行目において、a→bは前件肯定式に用いられてよい種類の式であるといえる。これらには①'の印をつけておこう。
4行目はa∧(a→b)=½ 、b=1で、a→bは1である。これは①の前半を完全には満たさず、また、肝心のa∧(a→b)=bが実現されていない。したがってこの4行目によって、ここに見てきた → は前件肯定式の重要な性質を完全には満たしていないということになる。
しかしここで、前件肯定式の近似式a∧(a→b)<bを考えれば、これについては満たしているといえる。このため4行目には①<という印をつけることにしよう。
こうして見てくると、束{0, ½, 1}の全体では、aが0以外のときに前件肯定式における
a∧(a→b)=b
ではなく、それふうの
a∧(a→b)≦b
が成立しているという結論となる。
残念な結果にも思えるが、しかしここまでくると、先にあげたハイティング代数の定義の意味が少し見えてくる。それは先の定義式は、この前件肯定式の近似を表現するものであったということである。再掲すると、
定義式①
束の任意の元 a, b, c, x について
(a∧x)≦b ←→ x≦c
であるような元cが存在する束をハイティング代数と呼び、このcをa→bとする。
(以下、←→ の左側の式を定義第1式、右側を定義第2式と呼ぶ)
ここで、定義第1式左辺のxをa→bに置き換えると、これは上で、束{0, ½ ,1}で成立を確認したa∧(a→b)≦bそのものである。つまり定義式のxというのはa→bの代用と解することができる。
このことから定義第1式左辺の前件肯定式風の式は、古典論理の前件肯定式の妥協版といえるが、しかしこれがハイティング代数の定義として述べられているということは、このa∧(a→b)≦bを、ここで → の定義のために用いてきた前件肯定式の内容とするということにほかならない。
そしてこの前件肯定式の近似式を用いて定義された → を、古典論理の条件法⊃に代わる直観主義論理の条件法とするということである。(直観主義論理で変わるのは前件肯定式ではなく条件法。前件肯定式は妥当式。)
定義第2式についても同様にして調べてみよう。第2式 x≦c については次のように理解できる。
任意の整数p,qに、常にp≦qの関係を成り立たせたい場合は、qの値をpが取り得る値の最大にしておけばよい。
定義第2式はこれを意味しており、上と同様にxをa→bに置き換えると、
(a→b)≦c
となるが、この式が成り立つためには、cは、少なくともa→bが取り得る値の最大の値でなければならない。そしてこの式は双条件の第2式として置かれているのであるから、当然、成り立つことが求められている。
しかしa→bの最大値をとるとはどういう意味なのか。
ここまで定義式のxにa→bを代入してきたが、実は、そのa→bというのは、ここで最終的に定義されようとしている直観主義論理におけるa→bそのものではない。そうではなくその「候補としてのa→b」である。
ハイティング代数定義の終わりに「このcをa→bとする」とある。つまり、真の「a→b」はxではなくcである。
x≦cを満たすようなxすなわち「a→bの候補」は複数あり得るが、それら候補の中の最大のものをcすなわち正規の「a→b」とするというのが
x≦c
の意味である。
つまりcはxと無関係な変数ではなくxの中のいずれかであり、x≦cと置くことで、その中の最大値を意味するものとなっている。x≦cが常に成り立つようなcとはxの最大値に他ならないからである。
ここで最大値を採用するのは、a∧(a→b)≦bをできるだけa∧(a→b)=bに近づくものにしたいためである。なお、ここでa→bとして定められたcは「相対擬補元」と呼ばれる。
ここまでの状況をハイティング代数の表で確認してみよう。確認したいのはa→bの候補としてのxと、その最大値cの状況。また、aが0以外のときにa∧(a→b)=bあるいはa∧(a→b)≦bが成立している状況である。
ハイティング代数を{0, 0.5, 1}とすると、aとbが取る値はそれぞれ3個なので、そのすべての組み合わせを作ると9行の表となる。
→ 演算を「閉じている」、つまり、→ の演算結果が束 {0, 0.5, 1} 内にとどまるとすると、a→bすなわちcの値は 0, 0.5, 1 のいずれかであり、a→bの候補としてのxもこのいずれかである。
ただしここではxに制約を設けず、xの値は0~1の間で無限にとることができると考える。xの数がある程度多い方がxの最大としてのcということがイメージしやすいからである。ここではa→bの候補値を0から0.1刻みの1まで x0~x10 の11個のxを設定し、x0=0、x1=0.1 ... x9=0.9、x10=1 のようにする。
例えば、
(1行目)a=0、b=0のとき、a→bの値は 0, 0.1 .... 0.9, 1 のいずれかである
(2行目)a=0、b=0.5のとき、a→bの値はやはり 0, 0.1 .... 0.9, 1 のいずれかである
:
ということである。
このようにして、a→bの候補値xすべてを書き出したのが下の表である。
さて、この中でどのxがa∧(a→b)≦bというハイティング代数定義式の制約を満たすか、すなわちa→bの候補となれるxなのかを見てみる。
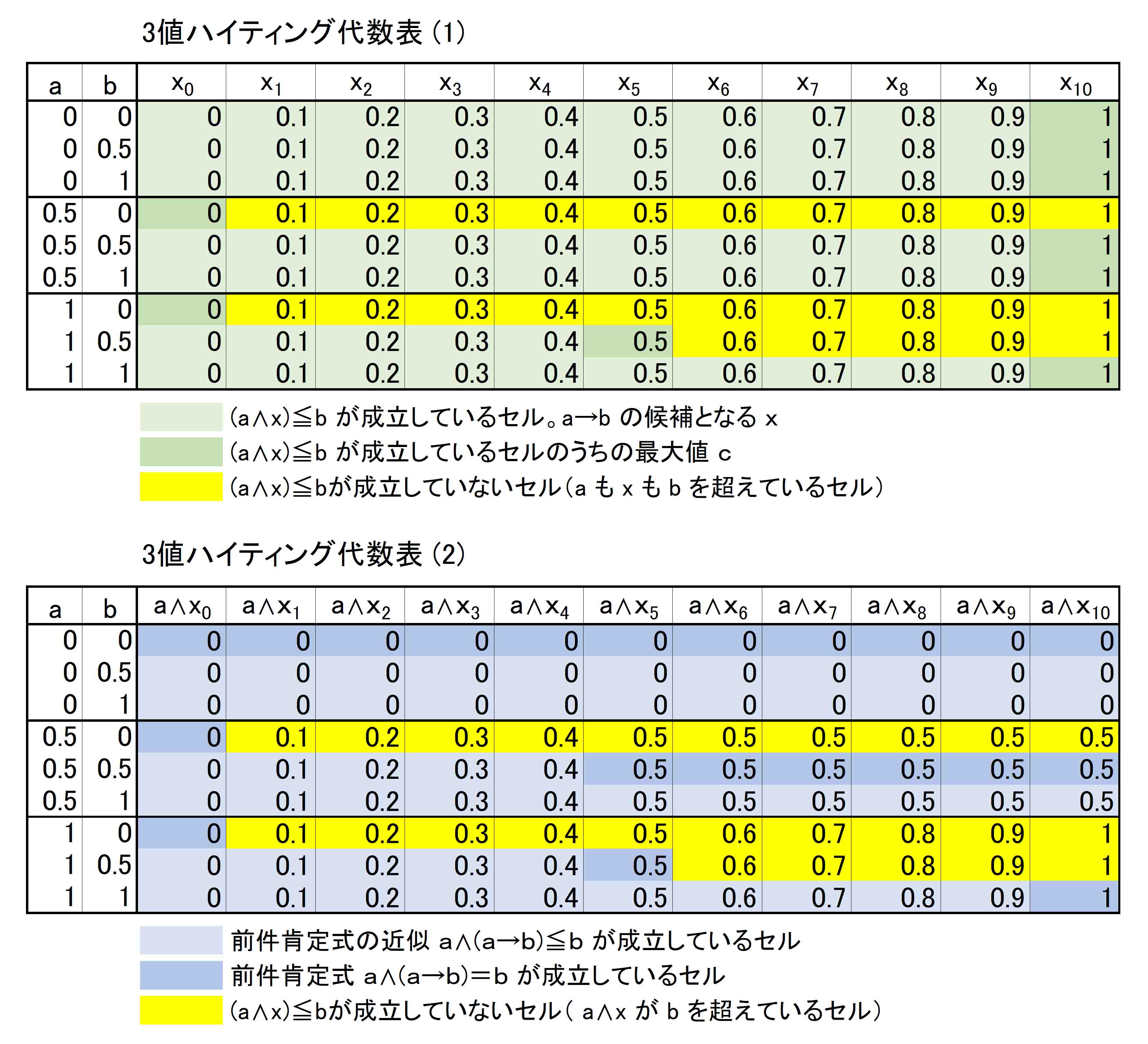
表(1)と表(2)の表内数値の関係を確認しておくと、表(1)は単に0から1の値を0.1刻みにxに割り振ったものである。表(2)は表(1)のそれぞれのxにおけるaとの下限(a∧x)を示したものである。
そこで、どのxがa∧(a→b)≦bを満たすかを見るために、まず表(2)でa∧xとbの大小関係を確認する。
a∧xの値(aとx0~x10 の小さい方)とbを比較していくと、黄色のセルで(a∧x)>bとなり式が破られている。例えば、a=1、b=0.5の行では、a∧xが0.6になるところで、(a∧x)=(1∧0.6)=0.6>0.5=bとなって(a∧x)≦bが成立しなくなる。
この黄色の状況をそのまま表(1)に移すと、黄色のセルのxが(a∧x)≦bを破るxであることになる。例えば、a=0.5、b=0の場合ではx1~x10 にはa→bの資格がないということである。
表(1)で黄色以外のセルが(a∧x)≦bが成立しているxであり、その最大を濃い緑色にしている。この濃い緑色の値がa、bの状況に応じて定まるc、つまりa→bの値である。
すなわち、a=0のときは、すべて c=1
a=0.5 b=0のとき、 c=0
a=0.5 b=0.5のとき、c=1
a=0.5 b=1のとき、 c=1
a=1 b=0のとき、 c=0
a=1 b=0.5のとき、c=0.5
a=1 b=1のとき、 c=1
である。
aとbがこれら一連の値をとるときに上のcの値となる演算を、→ 演算として定義したのが直観主義論理であるということになる。
前件a=0のときはa⊃b=1とし、前件a=1で後件b=0のときa⊃b=0とする古典論理の⊃の働きが保たれているのが分かる。ただし古典論理ではaが真の場合、すなわちaが0以外の場合にa∧(a⊃b)=bが成立していたが、この点を表(2)で見てみると、a=0.5、b=1の行には濃い青色のセルがない。つまり、このときa∧xの最大は0.5止まりでありbの値1に届いていない。(a=0、b=0.5の行と、a=0、b=1の行も濃い青色のセルがないが、これらはaが0なのでa∧(a→b)とbの値は一致していなくてよい。)
3値ハイティング代数表はこのように、直観主義論理においてaが0以外の場合であってもa∧(a→b)=bではなく、a∧(a→b)≦bが成立するのみであることを示している。古典論理でaが0以外というのはaが真であることを意味するが、直観主義論理ではaが0.5の場合もあり、そのときたまたまbが0.5であれば=が成り立つが、bが1の場合にはそうならないということである。
また表(2)からは、先に「(xの)最大値を採用するのは、a∧(a→b)≦bをできるだけa∧(a→b)=bに近づくものにしたいため」と説明した状況も見てとれる。例えば、a=0.5、b=0.5の行ではすべてのxにa→bの資格があるが、その中の最大であるx10 がcに採用されていることでa∧xの値がbと等しくなっている。
前段のハイティング代数表では、ハイティング代数の定義が実際にどのように実現されているかを見たが、これをグラフに表すとcの定義の成り立ちが分かり、定義式の意味をイメージできるようになる。次段に見る「ガロア接続」の予習にもなる。
以下、図1~図6で、縦軸xはa→bの候補を示し、縦軸a∧xはaとxの下限を示している。
3値ハイティング代数表と同様、xが取り得る値の範囲をx0~x10 の11個としている。

→ の定義にMP(前件肯定式)を利用する。a∧(a→b)=bにおけるa→bはこれから定義されようとしているものなので、これをxとし、a∧x=bとなるxをa→bとして定めたい。しかし、a∧x=bとなるようなxを定めることは望めないかもしれないので、その近似式a∧x≦bを満たすxをa→bとすることにする。
ただしそのようなxは複数あり得るのでa∧xのxはa→bの候補であるにすぎない。ここでは0から0.1刻みで1までx0~x10 の11個を考える。
定義の第一段階
xをa∧xにする関数(写像)fを考える。(x0 からの写像をf0 とし、以下同様。)
図1のa=0.5 b=1の場合、a∧x0~a∧x10 までのすべてがb以下の値となることがグラフで確認できる。
定義の第二段階
MPを満たす資格があるa∧xの範囲が分かったところで、これら資格があるa∧xについて、a∧xをxに戻す逆写像f-1 を考える。(図2)
この逆写像によって得られたxは、MPを満たすa∧xから作られたものなので、いずれもMPを満たすxである。
a∧xにおいては、aが何であれ、MPの資格を有するxの最大のものがa∧xをbに近づかせるので、逆写像f-1 から得られたxの中の最大のものをa→bとして定義する。このxが定義式のcに相当する。
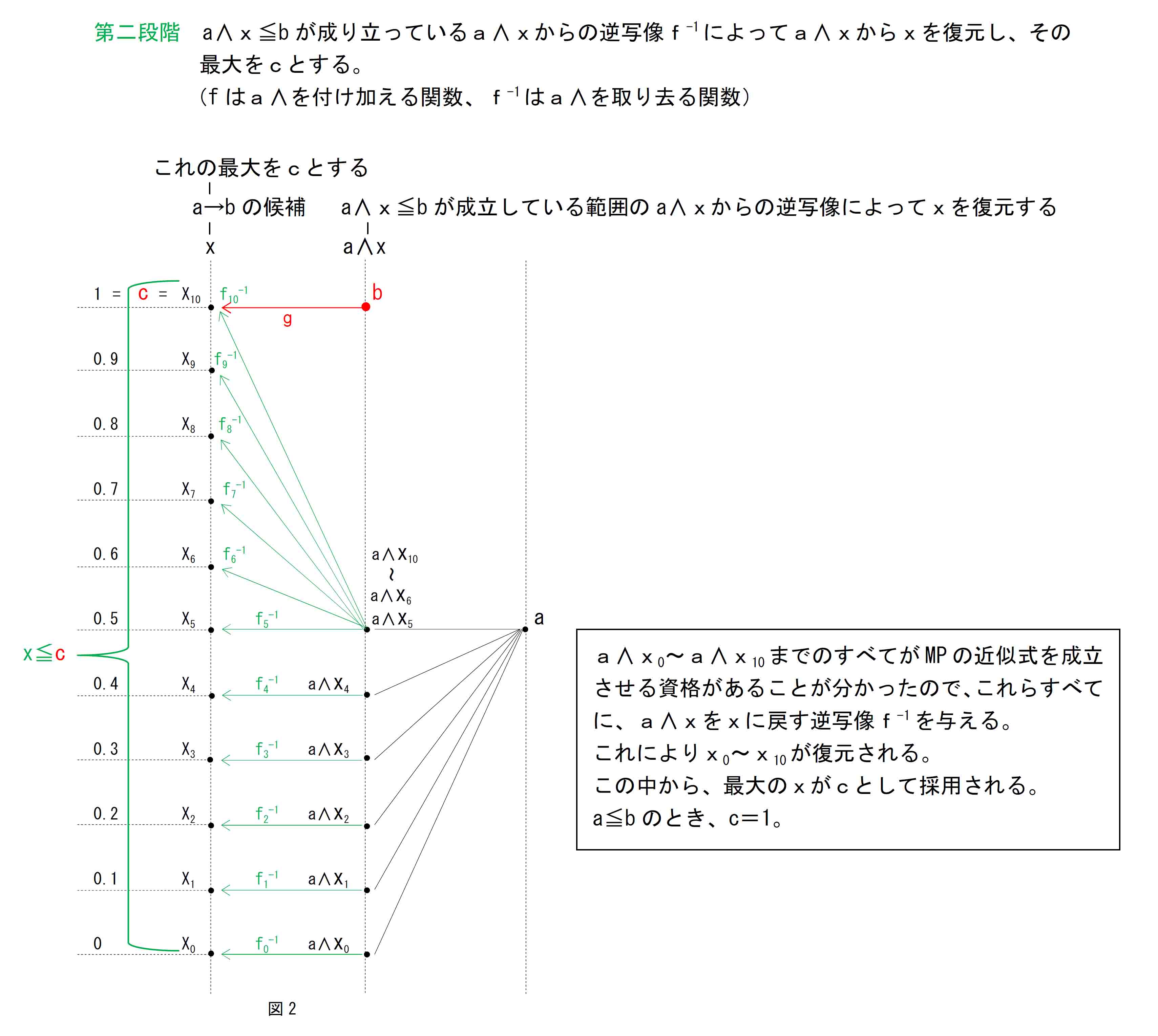
写像fでa∧xを得てそれをbと比較することにより、MPの資格のあるa∧xを限定しておいて(第一段階)、そこからの逆写像f-1 でxを復元することで、MPに最も近づくことができるxを特定する(第二段階)。
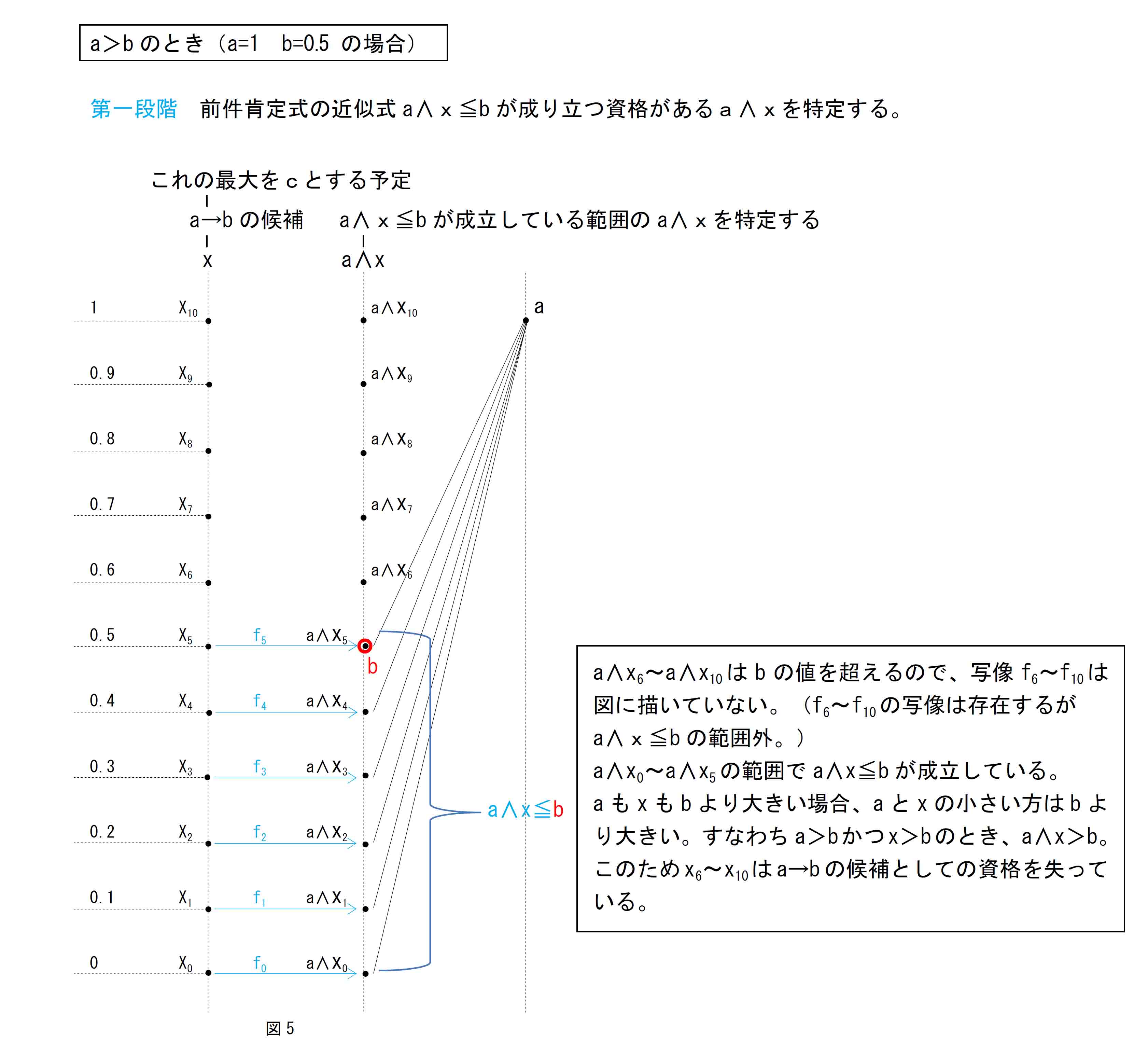
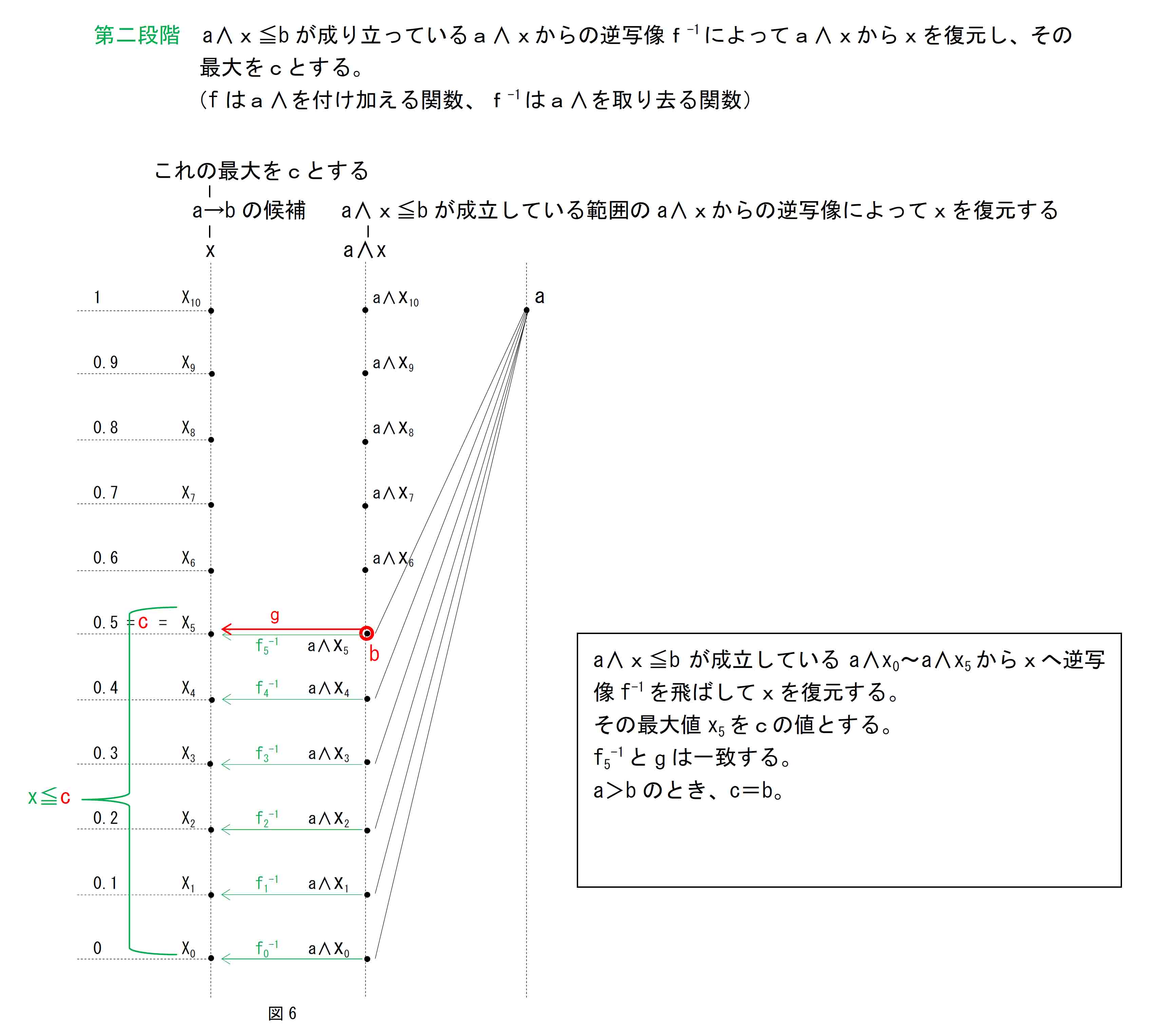
図1、図2のa=0.5 b=1の場合は、すべてのa∧xがb以下になるので、xを写像fでa∧xとした後、そのa∧xを逆写像f-1で単に元に戻しているだけのように見えるが、xをa∧xとする写像fによってMPの篩いにかけている。その篩いを通ったa∧xだけを逆写像でxに戻すということ。全部が篩いを通るのではない状況は、a=1 b=0.5など、a>bの設定で確認できる。(図5)
図1と図2の関係は「ガロア接続」と呼ばれる。通常、「ガロア接続」を説明する図では、図2のf-1 の過程を端折ったものになっているが、上図および後出する図ではf-1 の過程を表示している。
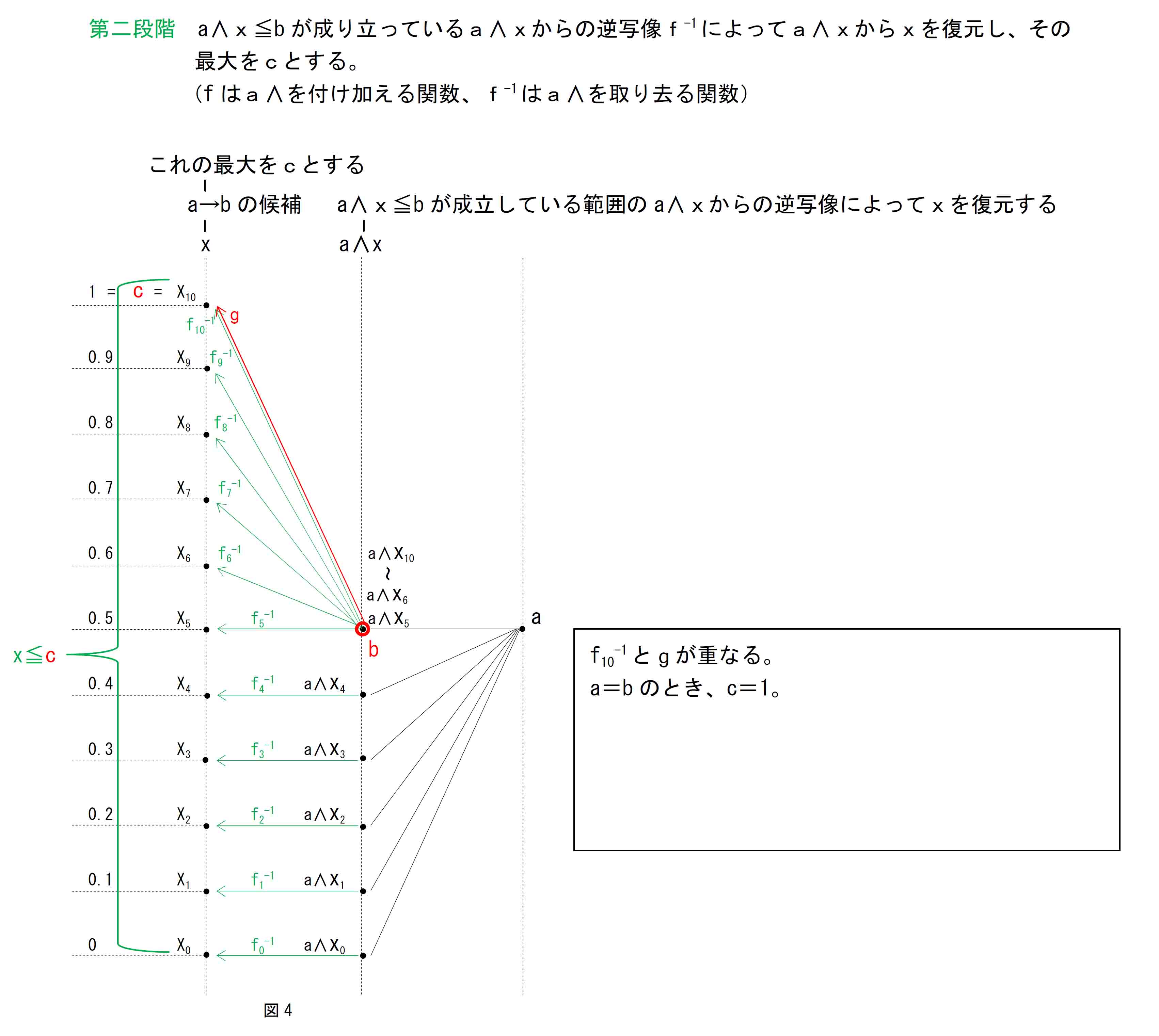
a=0.5 b=1の場合は、「ガロア接続」の写像 g(図2の x10 ← b) と、a∧x10 からの逆写像f-1 は一致しないが、これ以外のa、bの値の場合はgとf-1 は一致することが確認できる。(この点は(6)での「直観主義論理a∧(a→b)の真理表2」の4行目、また、3値ハイティング代数表(2)の6行目がMPでの=を実現していないこととして確認していた。)
仮にa、bの組み合わせすべてにおいて、gとf-1 が一致すれば図1と図2の関係は「同型写像」となるが、a=0.5 b=1の場合は一致しないので、ハイティング代数は「ガロア接続」というより緩い関係にとどまる。
ここでは写像gを、bをcにする関数として理解しておく。(関数gの全体は次段で確認する。)
bは「理想のa∧(a→b)」であり(∵a∧(a→b)=bとなることが理想なので)、cは「正規のa→b」である。したがってgを言いかえれば「理想のa∧(a→b)」を「正規の(a→b)」にする関数であり、gは「a∧」を取り去るf-1 と同種の関数といえる。

ガロア接続とは、対応する二つの集合間において、それぞれの順序関係が保たれるような写像(関数)でのやりとりが成立する状態をいう。
ある集合A {a, b, c. d} を関数fによって、別の集合Bに {f(a), f(b), f(c), f(d)} として移行する。このとき集合Aでの a, b, c, d の順序が、集合Bにおいて f(a), f(b), f(c), f(d) として保たれるとする。ここで集合Bの f(a), f(b), f(c), f(d) を逆関数f-1によって元の集合Aに戻せば、A内に復元された a, b, c, d の順序は元のまま保たれる。このような二つの集合間のやりとりは「同型写像」と呼ばれる。
ガロア接続は、BからAへの戻し写像が単純厳格な逆写像f-1ではないが、ある写像、例えば何らかの工夫を凝らした写像gを使えば、Aに戻したときの f(a), f(b), f(c), f(d) つまりg(f(a)), g(f(b)), g(f(c)), g(f(d))を、元の a, b, c, d の順序のまま保つことができるというものである。
式で表すと次のようになる。
Aでの順序 Bでの順序
x≦g(y) ←→ f(x)≦y
言葉で言うと――Aの任意の元xを関数fでf(x)に変換してBに移行した後、移行したそのf(x)よりも大きいBの元yを、ある関数gでg(y)に変換してAに戻す。このときAでのそのg(y)が初めの元xより大きくなるということが、すべてのx、yについて成り立つような関数の組f、gが存在する――ということである。
ハイティング代数では、このガロア接続が成立している。
x≦c ←→ a∧x≦b あるいは
x≦a→b ←→ a∧x≦b
a∧xを、xが関数fによってa∧xに変換されたもの、つまりf(x)とみる。また、a→bを、bが関数gによってa→bに変換されたもの、つまりg(b)とみれば、(4)のハイティング代数の定義式①はガロア接続そのものである。というよりも、定義式①はガロア接続によるハイティング代数の定義なのである。
ハイティング代数では写像fについてはaをa∧xにする関数、簡単に言えばaに∧xを付け加える関数であることが初めから定まっている。ただしfはa→bをbにする関数でもあって、a→bとbの関係は明らかではないので、この部分でfは完全には明らかではない状況にある。
また、写像gもf(x)については、a∧xをaに戻す、簡単に言えばa∧xから∧xを取り去る関数であり、fの逆写像f-1 であることが明らかである。しかしまたgは、bをa→bにする関数でもあって、fと同様、この部分については明らかではない。
したがってこの時点で、関数fもgも、aとxに関しては働きが分かっているが、ただbが関わる部分については別の働きをする関数であることが明らかであるものの、その内容は分かっていない。
以下では、ガロア接続が実現されるために写像gがbについてどのように働かなければならないかを説明する。fはa→bとbに関して写像gの逆写像であるから、bに関する写像gの働きが明らかとなってgの全体が分かればfの全体も定まるので、fについては改めて述べない。
なお、ガロア接続は2つの集合間の関係だが、ハイティング代数でのガロア接続は自分自身への往復写像である。下図では、往復写像として描くと見づらくなるので、写像を左から右への移行として描いている。左端と右端の枠は同一枠の描画であり、中央の枠も自分自身である。
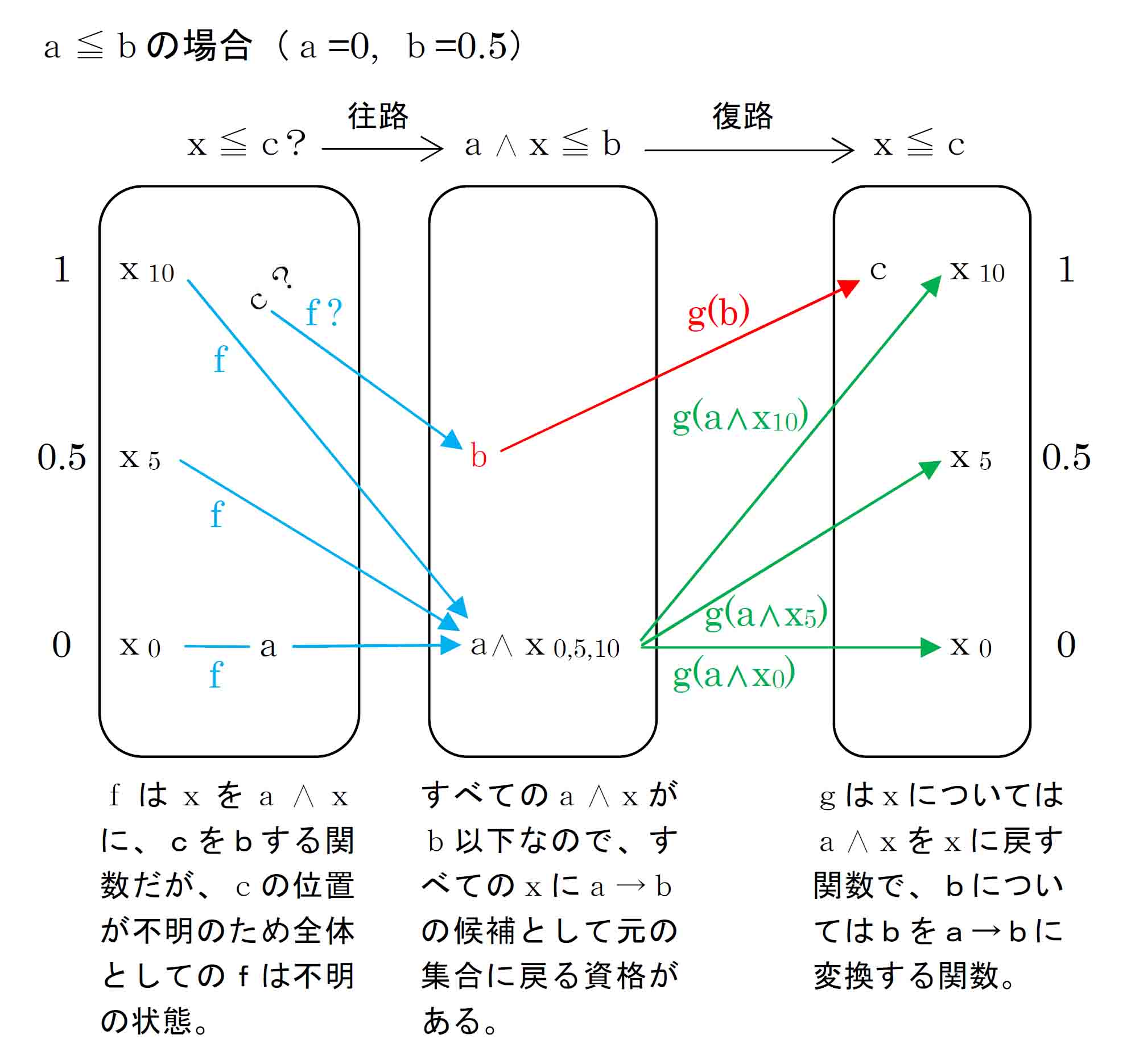
|
a≦bの場合、aおよびxがどんな値であっても、とにかくaがbより小さいのでa∧xは常にbより小さい。すなわち、すべてのxがa∧x≦bの関係を満たす。 したがってこの場合にbをcとして戻した先でx≦cを維持するためには、gはbを、このときxが取り得る最大の値である1の位置に戻してやらなければならない。この働きがg(b)である。 すなわちbについてg(b)=1=c=(a→b)。 a∧xをxに戻す際は、逆写像f-1によって元のxの大小関係を保つことができるが、bについては別の扱いをしなければならない。このため、この対応は同型写像ではなくガロア接続となる。 a≦bでの写像gは、bを1に戻す働きと、f(x)をf-1によって元のxの位置に戻す働きの二つを兼ね備えた写像となる。すなわちxについてg(f(x))=f-1(f(x))=x。 |
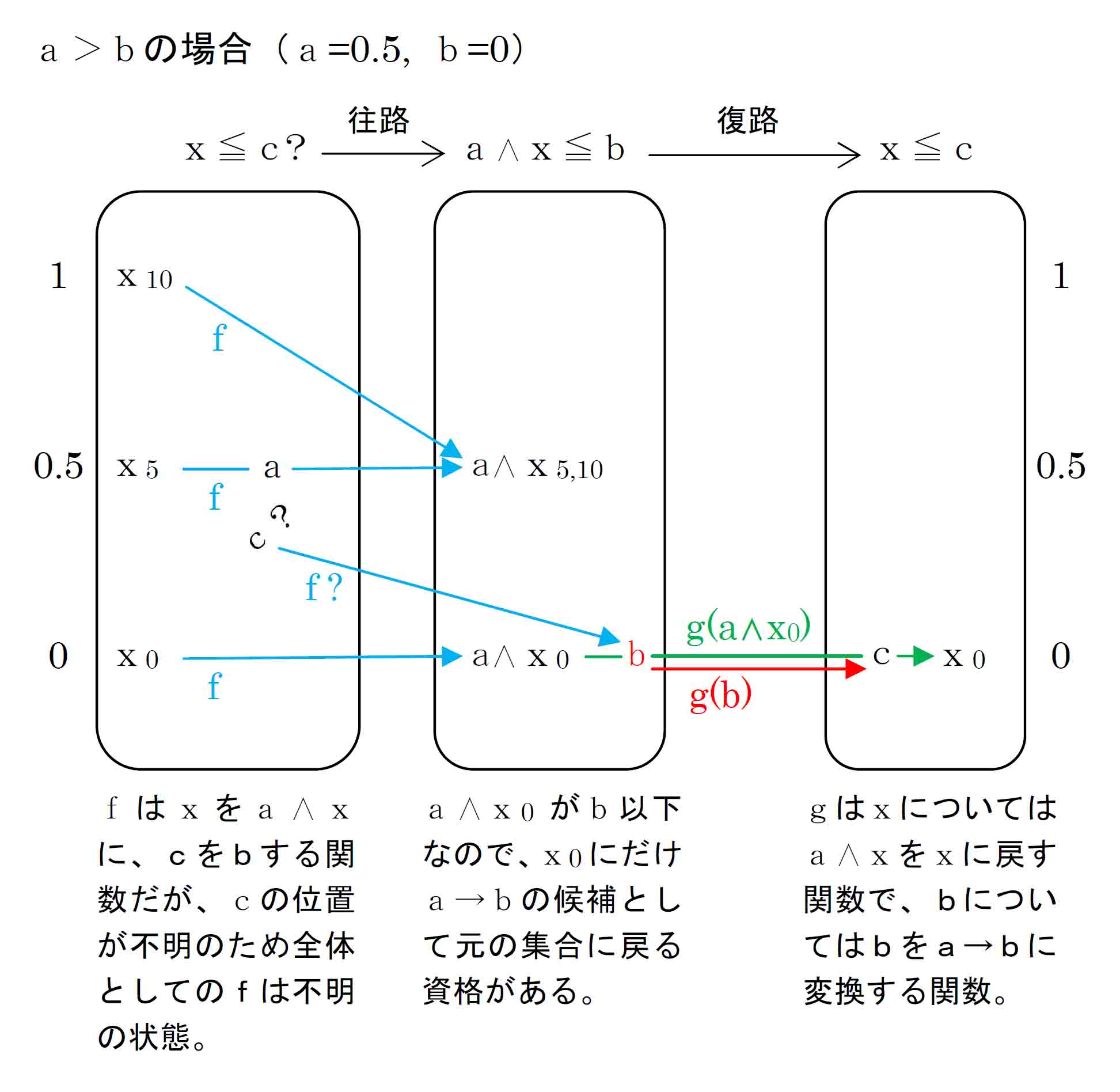
|
a>bの場合も、a∧xとbの大小関係をxとcの関係において保つためには、a≦bの場合と同様に、bを、a∧x≦bを保っている最大のxの位置に戻してやればよい。 ただしa>bの場合は、a∧x≦bの関係を満たすxが限られる。a=0.5、b=0の例では、a∧x≦bを保っているのはx0 のみで、これが最大のxである。 a>bであり、a∧x≦bが保たれるためには、すなわちaとxの小さい方がbより小さく保たれるためには(すでにaはbより大きいので)xの方がbより小さくなければならない。そのようなxの最大はx=bであるxなので最大のxの位置はbである。したがってbの位置にbをcとして戻してやればよい。 すなわちbについてg(b)=b=c=(a→b)。 a>bでの写像gは、bを元のbの位置に戻す働きと、b以下であるf(x)すなわちa∧xを逆写像f-1によって元のxの位置に戻す働きの二つを兼ね備えた写像となる。xについてのgはa≦bの場合と同じ。ただしa>bの場合、x≦bを満たさないxについては「a→bの候補」ではなくなりx自体存在しなくなるのでgも存在しない。 これらのことから先の図と合わせたガロア接続の写像gは、a≦bの場合とa>bで動作を分ける働きを持つ関数である。 |
ガロア接続は、下のハイティング代数の定義[第1式左辺]xと[第2式左辺]a∧xを関数fによって関連づけ、[第2式右辺]bと[第1式右辺]cを関数gによって関連づけることによって、定義式が持つ性質を簡明に捉えている。
x≦c ←→ (a∧x)≦b
関数f、gを使って表現すると、
x≦g(b) ←→f(x)≦b
となり、式からaとcが消えてxとbの一種不思議な関係が浮かんでくる。先に(4)の段でこのガロア接続に触れたところで「『随伴』などの深遠な概念」と書いた「随伴」というのは、fとgがもたらすこのxとbの関係のことである。
ここでf(x)はa∧xであり、g(b)はa→bだが、「随伴」は∧と→ の関係の深さを示した概念といえる。実際、古典論理ではaが真のときa∧bとa→bは同じ真理値を持ち、直観主義論理においてもaが1のとき両者の真理値は同じである。意味を考えればさらに明らかである。「aとbが起こる」ということと「aが起こればbも起こる」ということは、aが起きている状況では同じことである。
ここでのまとめとして、関数gとfの働きを、a≦b と a>b に区分けした3値ハイティング代数表で確認しておく。
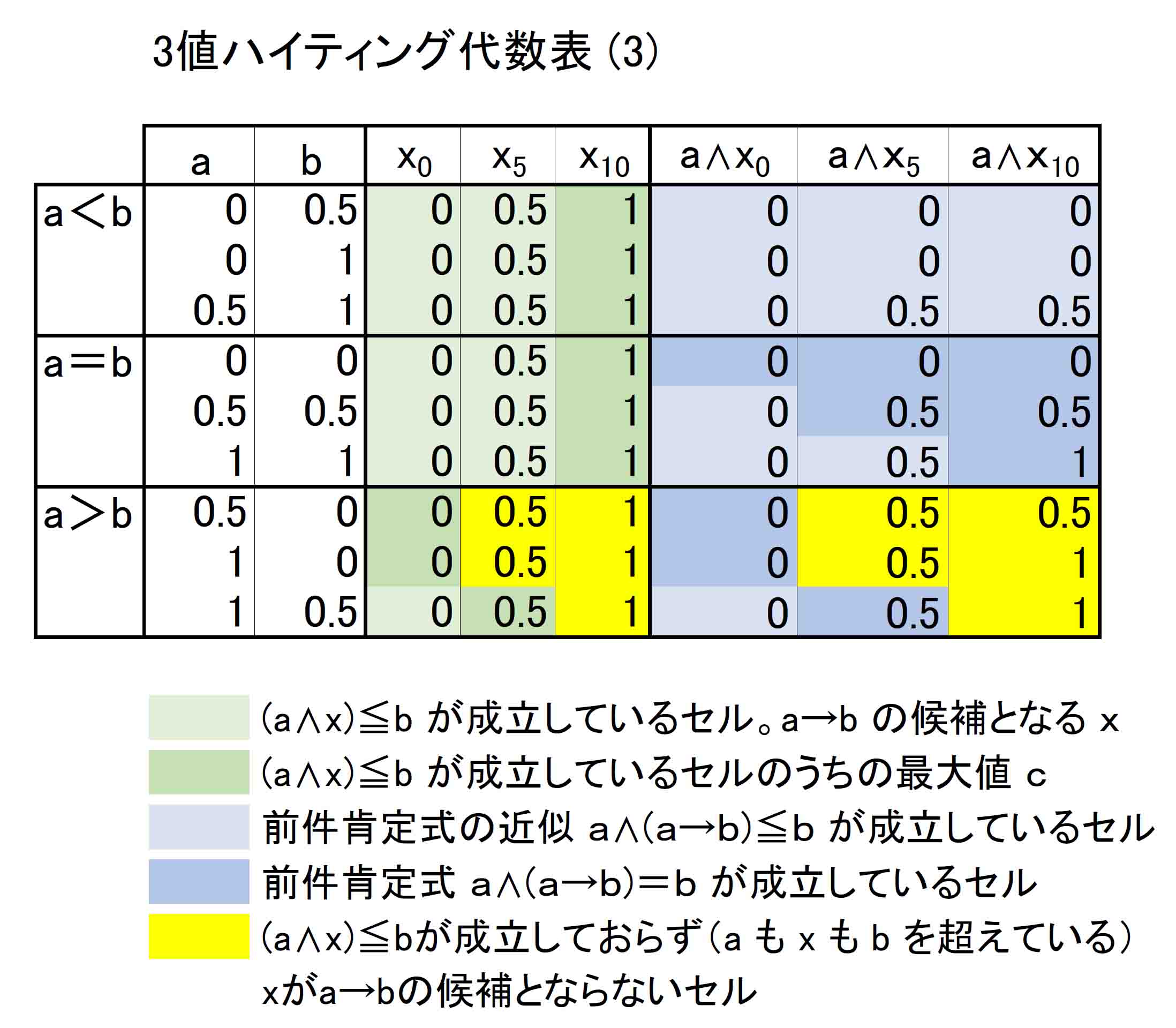
まず、すべての行でx≦cが成立していることを確認する。cはxの最大として設定されたものなので、これは当然のことだが、a≦bのときとa>bのときではcの値の成立の仕方が違う。
定義第2式x≦cが成立している行で(したがってすべての行で)、
a≦bの場合、
bをcにする関数gとは、0、0.5、1であるbをすべて1にしているのでg(b)=1である。
a>bの場合、
bをcにする関数gとは、bの値をもってcとしているので、g(b)=bである。
これらのときの定義第1式a∧x≦bの成立有無を数値から確認すると、
a≦bのときは、
xをa∧xにする関数fは、
x≦aの場合はf(x)=x
x>aの場合はf(x)=a
であることが確認できる。
つまりxがa以下ではf(x)=xだが、xがaを超えているときはf(x)=aで、f(x)の最大はaである。また、ここではa≦bが前提なので、これによりf(x)≦b、すなわちa∧x≦bが成立している。
a>bのときは、
xをa∧xにする関数fは、a≦bの場合と同様に、aかxの小さい方の値を採用するものとして働いている。ただしその最大はb止まりになっていることが確認できる。したがってf(x)≦b、つまりa∧x≦bが成立している。
以上によってガロア接続の関数g、fが働いている状況で、x≦cとa∧x≦bが同時に成り立っていることが確認できた。
以上、ハイティング代数 {0, ½, 1} の → の定義がどのように行われているかを見てきた。古典論理とは異なる条件法の定義についてとりあえず理解できたとしてよいだろう。
Hard study 5-2-4 で、「『論理学』では⊃の分子式の分析が慎重に避けられているように見える」と書いたが、実際にそうなのかはともかくとして、やはり直観主義論理の条件法には古典論理からの理解だけでは済まされない性質が含まれていたということである。
ただしハイティング代数を理解するということは、上で行ってきたように予めハイティング代数であるものを用意して、その性質を調べることから定義の成り立ちを理解するというだけでは十分ではない。
それ以前の問題として、ハイティング代数の前提となっている束の条件を理解する必要がある。ハイティング代数の外に出て、ハイティング代数が成立可能である束の範囲を知ることがハイティング代数の完全理解につながる。
この点は定義にも表明されている。
「元cが存在する束をハイティング代数とする」
上に見てきた「3値ハイティング代数表」では、a→bの候補としてのx1~x10には、その上限が0または0.5または1として存在した。この上限をa→bとして定めたが、しかしこのような元cが必ず存在するとは限らないということである。
では、このようなxからなる集合に上限が存在しない(共通上界がない、共通上界に最小元がない、上限が一意に定まらない等)とはどういう束であるのか。
ハイティング代数には、これまでに見てきた定義
① (a∧x)≦b ←→ x≦c あるいは
(a∧x)≦b ←→ x≦a→b
の他に、2つの定義がある。
束を{元∈束|元の性質} と表記すると、その一つめは束Hにおいて、
② Max{x∈H|a∧x≦b}が存在し、これをa→bとする
というものである。
これは、a∧xがb以下であるようなxの最大値の存在を述べた定義である。つまり①の定義のcの存在を述べたもので、①の第2式と第1式を合わせて1つの式に表現したものと解することができる。
二つめは、束Hの任意の元aとHの可算部分集合{b}において、(可算部分集合とは、{b1},{b2}...のように番号を割り当てることができる部分集合。ここでは簡略にbで表す。)
③ a∧Vb=V(a∧b) が成り立つ
というもの。ここで、Vは∨と同じ上限記号の一種で、集合のように一つの項において上限が存在するときの上限の書き方である。
また、{b}が付番できる集合として指定されているのは、③ではこれまでに見てきた有限束ではなく、無限を要素に持つことができる「完備束」を前提しているためである。(束の定義が任意の2元について上限と下限が存在するということであるのに対し、完備束では任意の部分集合について上限と下限が存在するという定義が行われる。)ただしここでは、束の拡張に伴って出てきた完備性や可算部分集合については置いておき、以下に注目する。
③は完備ハイティング代数において分配律が成立することを述べたものである。この式自体の証明は①の定義式を使って行うことができる。証明内容をたどったものを注に挙げておく。
また、①と②が同等であることの証明と、②と③が同等であること(厳密には②の完備版の定義と③が同等であること)の証明が、注[22]に引用した同書 命題5.1と命題5.9で確認できる。こちらも証明内容をたどったものを注に挙げておく。
さて、課題は①の定義における「a∧x≦bが成立するようなxの集合において上限が存在しない束とはどのようなものか」を知ることだが、上の三個の定義は同等なので、このいずれかが成立しない束が分かればよいことになる。
ただし、これまでに見てきたIの形の3値ハイティング代数モデル(次段(13)のハイティング代数モデル参照)では「上限が存在しない」ということはあり得ないので、したがってそれだけを見てきた我々としては、その事態をイメージできない状況にある。この点を考えれば、やはり定義①あるいは同じことを述べている②において、それが実現できない束というものを知りたい気がする。
『束論』(1966年初版)、『現代のブール代数』(1986年)などの古い書籍には、分配律やモジュラー律が成立しない束の具体例が掲載されている。モジュラー律というのは束特有の弱い分配律である。
したがって、ある束では定義③が成立しないことについてはこれらの書物に当たれば確認できるが、本来的には、その束において定義①②が成立しないことを理解したい。「上限cが存在しない」というのがどういう事態であるのかをイメージしたいためである。しかしとりあえずは、ある束では定義③が成立しないことを以下の通り確認しておこう。
分配律が成立しない束の一つは、いびつな五角形に5値が配されたもので、上端を1、下端を0とし、仮にこれをD形と呼ぶと、Dの弧上に相当する2つの頂点にa、xが置かれ、直線的な縦棒の中程にbが置かれている束である。いずれの2点をとっても上限、下限が存在し、したがってこれが束であることについては明らかである。
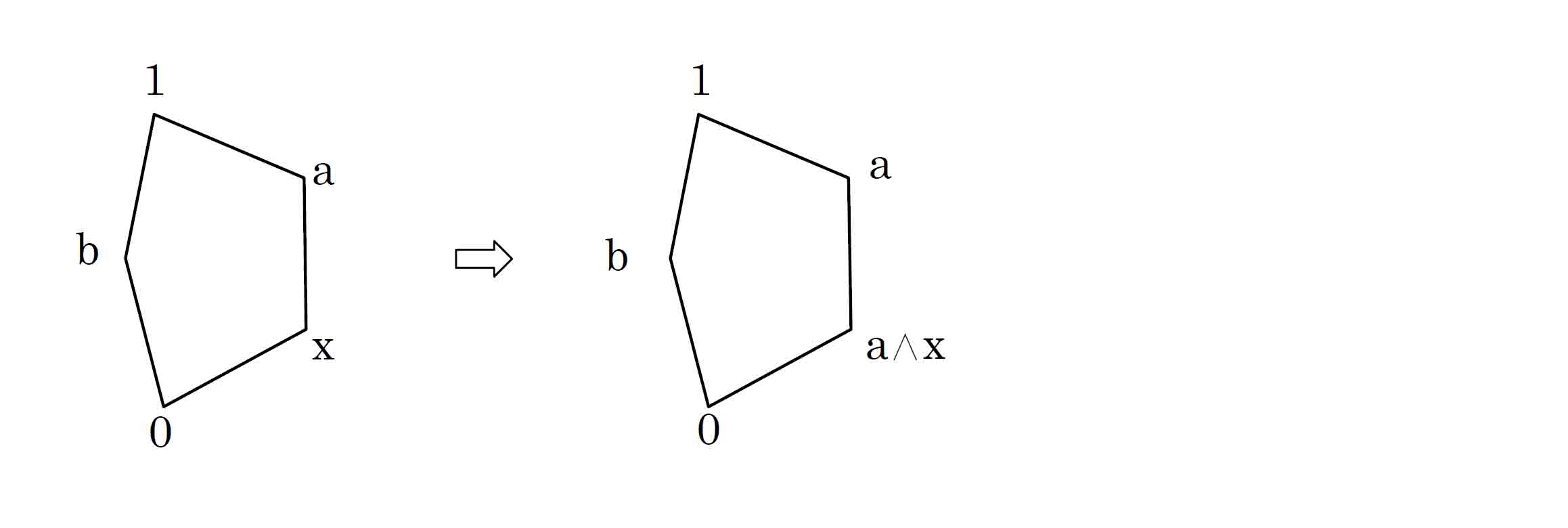
上図でaとb間、xとb間に順序関係はない。aとxの下限(a∧x)はxとなるが、xとb間の大小比較ができないので、a∧x≦bというハイティング代数定義①の基準の論外的状況が生じている。
先に、上限が存在しない例として「共通上界がない」「共通上界に最小元がない」「上限が一意に定まらない」という思いつく限りのことを挙げていたが、考えてみれば前二者については「上限がない」ことになるので、そもそも束ではなく見当違いである。
そういうことではなく、上図のように束でありながら、a∧xとb間の順序関係が存在できない場合があり、「cが存在しない」少なくとも一つの例がこれだということである。
なお、先段(10)の図5では、a>bかつx>bのとき、a∧xのxが、a→bの候補としての資格を失っていることを確認したが、その状況がcが存在しないケースの一つであるというわけではない。そこでは、ただa→bの候補xが、a≦bである場合や、a>bだがx≦bである場合とは異なり、a∧x≦bによって、すなわちa∧xとbの比較によって限定される事態が起きているということであり、これは候補xの中からa→bを特定しようとする操作の過程で生じる除外であり、定義が実行できているその過程に生じる事態であるにすぎない。
これに対して、上の5角形の束で起きているのは、a∧xとbの比較そのものができない、つまり定義が実行できないという事態である。
この束は、また、ハイティング代数定義③に表れているモジュラー律を満たさない。モジュラー律は、x≦aのときに、
(x∨b)∧a=x∨(b∧a)
というように、左辺と右辺のx、b、aの並び順が同じ、∨と∧の位置も同じで、ただカッコだけがずれる形となるある種の分配律である。
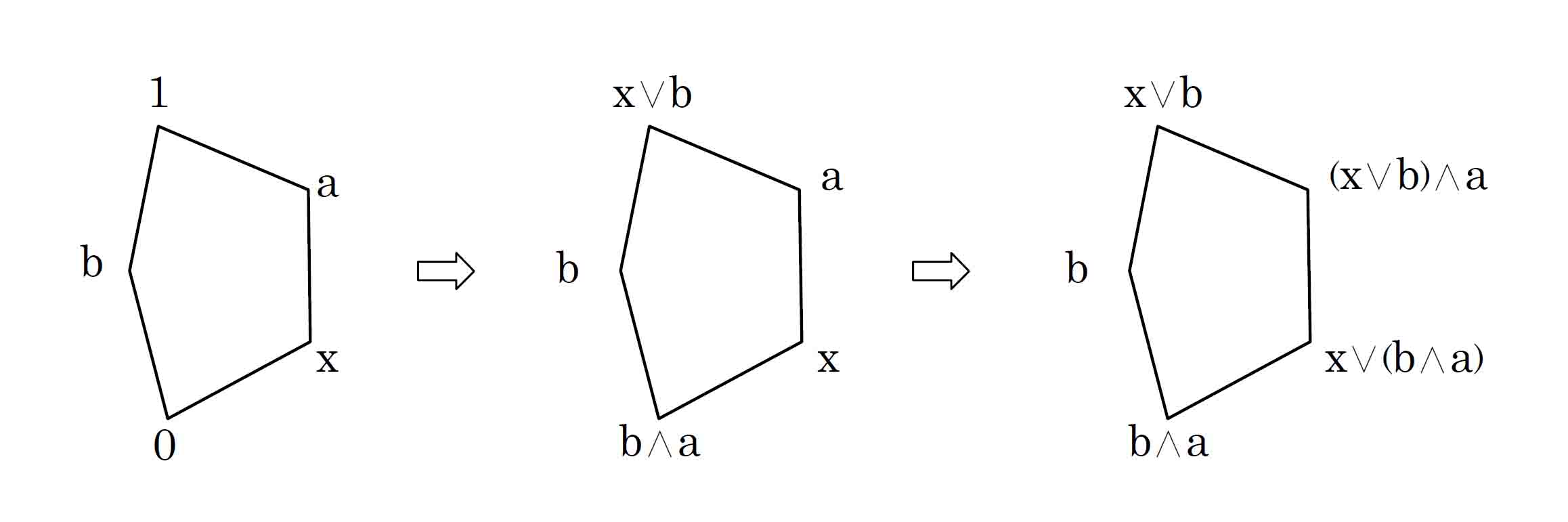
上図で、xとbの上限は1、したがって(x∨b)∧a=a。bとaの下限は0、したがってx∨(b∧a)=xとなり、(x∨b)∧aとx∨(b∧a)は=で結ばれない。
この束が一般の分配律を満たさないことも容易に見てとれる。分配律は、
a∧(b∨x)=(a∧b)∨(a∧x)
だが、b∨x=1なので、左辺は
a∧(b∨x)=a∧1=a
右辺の第1項はa∧b=0。右辺の第2項はa∧x=xなので、
(a∧b)∨(a∧x)=0∨x=x
したがって、左辺がa、右辺がxでモジュラー律と同じ結果となり分配律は成立していない。
先の『束論』に紹介されている分配律が成立しないもう一つの例は、◇の中央に縦棒があるモデルで、上端を1、下端を0とし、その中間位置にa、b、cを横並びに配置したものである。この束では、モジュラー律は成立するが、分配律は成立しないということである。
モジュラー律 (x∨b)∧a=x∨(b∧a) では「x≦aのとき」という条件が付くので、xを0のところに配置して確認する。(xをaのところに置いても同様の結果となる。)
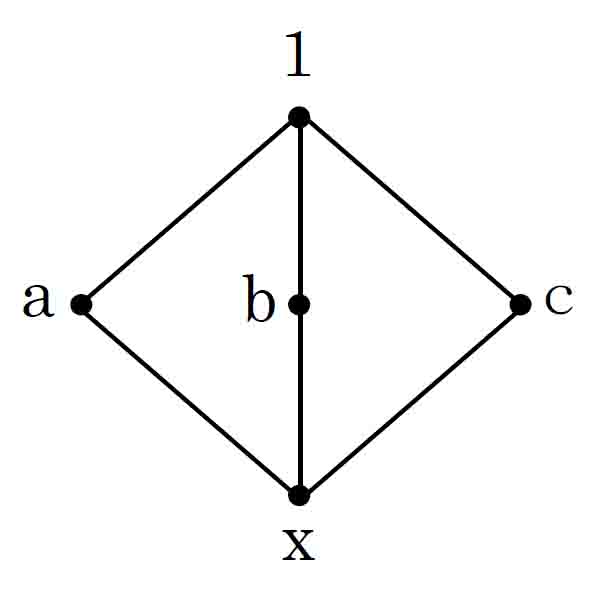
左辺(x∨b)∧a=b∧a=x
右辺x∨(b∧a)=x∨x=x となり成立している。
分配律a∧(b∨c)=(a∧b)∨(a∧c) では、
左辺a∧(b∨c)=a∧1=a
右辺(a∧b)∨(a∧c)=x∨x=x となり成立しない。
縦棒ありの◇形束では、すべての元の比較ができるとしても(a、b、cそれぞれを0.5の値を持つものとしても上の状況が成立する)、分配律が成立していないためにハイティング代数にならない。5角形束との共通点を考えれば、ハイティング代数にならない、すなわち「上限cが存在しない」というのは、元同士の比較ができないということであるよりも、分配律が成り立たないことにあるということになる。
先に挙げた見通しを拾うと、分配律が成立しないとは「上限が一意に定まらない」ということであり、それが「上限cが存在しない」ことの意味だと思われるが、確認ができれば追記したい。また、この2つの非分配束以外の例についても知りたいところだが、今回は以上で満足することとしたい。
ブール代数の補元に相当するハイティング代数の補元は「擬補元」と呼ばれ、次のように定義される。
¬x:=x→ 0(:=は定義の意味)
上の定義で使われている → は、ハイティング代数の定義で定めた → である。すなわち、その定義は、a→bの候補xにおいて
a≦ bのとき、x≦1
a>bのとき、x≦b
が成り立つ最大のxを正規の「a→b」の値とするということであった。つまり、左辺のxをa→bに置き換えたときの値とは、その最大値であるから、
a≦ bのとき、a→b=1
a>bのとき、a→b=b
である。ハイティング代数の最小元が0であることを踏まえて、このa→bの定義を、¬xの定義x→ 0 にそのまま置き換えると、¬xとは、
x≦ 0のとき、すなわちx=0のとき、x→ 0=1。したがって ¬x=1
x>0のとき、すなわちxが0以上のとき、x→ 0=0。したがって ¬x=0
ということになる。
これによってハイティング代数 {0, ½, 1} の¬の真理表は以下になる。

x=½を意味づけして、例えば「現時点では未証明だがやがて証明される」と解すると、¬x=0は「現時点で未証明で将来的にも証明されない」といった意味合いになる。
これは3値ハイティング代数の½をクリプキ意味論の認識史01(α⊮、~β⊩)相当と見たものだが、「直観主義論理の¬Pの証明表」で確認すると(Hard study 5-2-4)、¬xの認識史01は確かにα⊮、~β⊮であり、「現時点で未証明で将来的にも証明されない」という上の解釈に一致している。
参考までに、ウカシェヴィチの三値論理の¬の真理表は以下のようである。

こちらはx=½を「『彼は生きている』という情報はあいまいである」という意味に解すると、¬xは「『彼は死んでいる』という情報もまたあいまいである」という意味に解することができる。½の解釈にはいろいろな可能性がある。
さて、以上で、ハイティング代数の「擬補元」¬については一件落着とも思える。しかし一筋縄ではいかないのがハイティング代数である。
当節冒頭に紹介したWEB文献に掲載されているハイティング代数モデルは以下である。
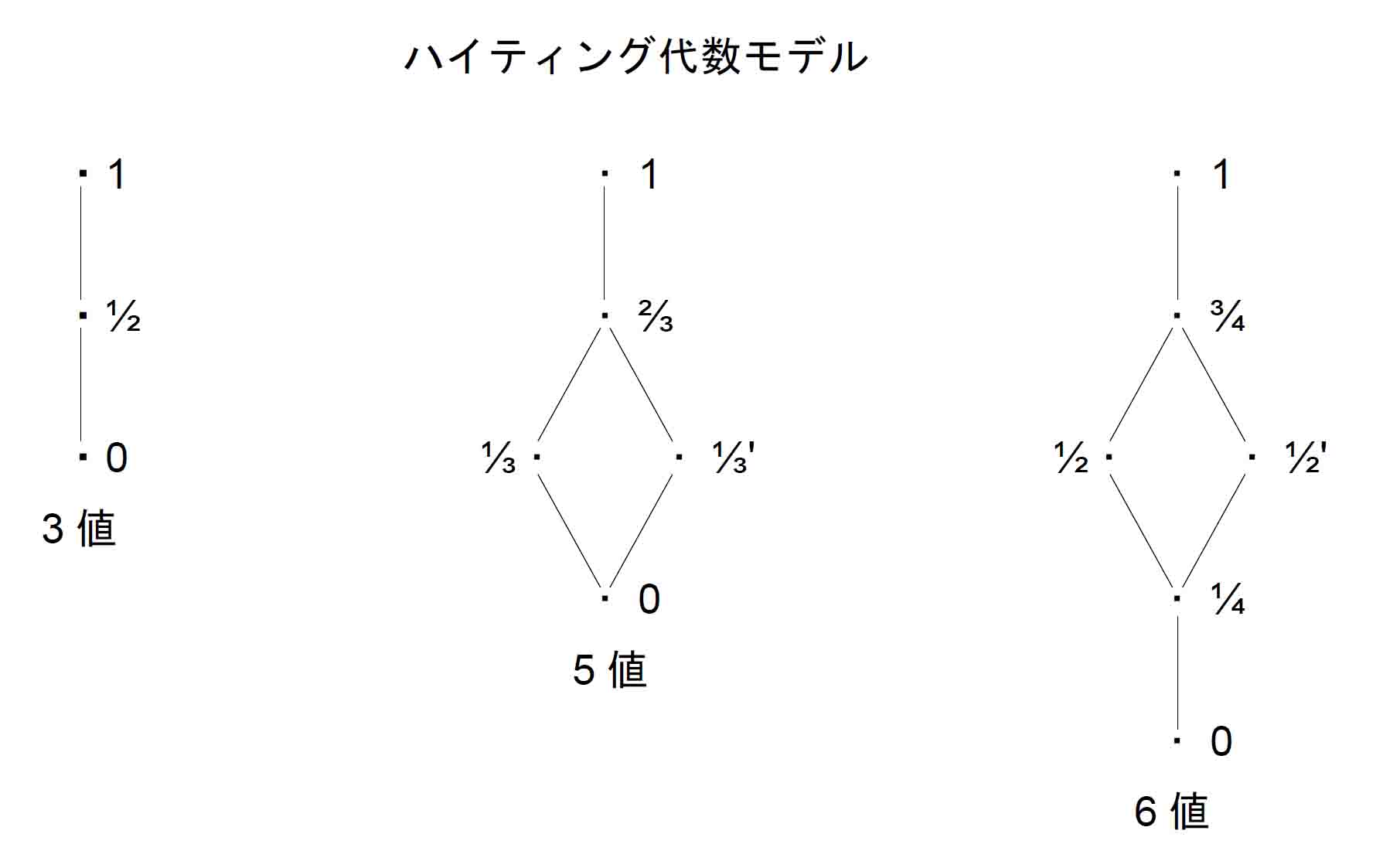
左端のモデルはこれまでに扱ってきた {0, ½, 1} がI形に並んだもので、これをハイティング代数3値モデルと呼ぶことにする。
真中は5値からなるハイティング代数で5値モデル、右は6値モデルと呼ぶ。また、ここで新たに登場した真中と右のモデルがハイティング代数であることの確認は省略する。(分配律が成立していればハイティング代数である。)
注目したいのは、それぞれの否定のあり方である。
当該WEB文献では、
3値モデル ¬1=0、¬½=0、¬0=1
5値モデル ¬1=0、¬⅔=0、¬⅓=⅓'、¬⅓'=⅓、¬0=1
6値モデル ¬1=0、¬¾=0、¬½=0、¬½'=0、¬¼=0、¬0=1
となっており、続けて
「0以外の元の擬補元は0になることが多いようですが、例外もあります。」
とだけ書かれている。この他の説明はないので検討してみると以下のことが分かる。
まず、どのモデルにも、
¬1=0、¬0=1
というブール代数的な否定がある。
また、どのモデルにも、
¬½=0、¬⅔=0、¬¾=0、¬¼=0
のように、当段冒頭に見たハイティング代数の擬補元の定義から導かれている否定がある。もっともブール代数的否定もこの定義から導かれたものなので、両者を同等と見ることは可能である。
5値モデルには、ブール代数的でもハイティング代数的でもない否定
¬⅓=⅓'、¬⅓'=⅓
がある。これが先の説明で「例外もあります」と言われていたものである。
この⅓とシングルクォート付きの⅓'は、上に見たウカシェヴィチの三値論理の否定と同じ種類のもののようにも見えるが、ウカシェヴィチでは ½ → ½=1で、5値モデルでは ⅓ → ⅓'=0、 ⅓' → ⅓=0として計算されるので両者は全く別種のものである。(同WEB文献のプレ線型性式「A→B.∨.B→A」での計算に見られるこの ⅓ → ⅓'=0、 ⅓' → ⅓=0 は誤りであることが判明。これに伴い旧稿を以下に訂正[2025年8月]。)
上の5値モデルでは、⅓ と ⅓' との間には順序関係が存在していない。そのため ⅓ → ⅓' では、前件後件の大小から値が決まる3値モデルでのような簡潔な → 演算を行うことができない。そこでハイティング代数定義①に立ち戻ると以下。
定義① (a∧x)≦b ←→ x≦a→b
aに ⅓、bに ⅓' を代入すると、
(⅓ ∧x)≦⅓' ←→ x≦ ⅓ → ⅓'
ここで⅓ → ⅓'、すなわちa→bはa∧x≦bを満たす最大のxというのが定義式の意味である。定義式 x≦a→b が、a→bをxの最大のものとして定める式であることは、当節「(8) 定義第2式 x≦c の意味」で解説したところである。
すなわちa(= ⅓ )と∧演算を行って、b(= ⅓' )以下となるxのうちの最も大きいxがa→bの値、つまり、ここで求めたい ⅓ → ⅓' の値である。
ハイティング代数5値モデルでは、⅓ に∧演算を行って ⅓' 以下になる(5値モデルの形から ⅓' 以下とは0のこと)、すなわち0になる∧の相方は、0だけではなく⅓' もある。⅓ ∧ 0=0 だが、⅓∧⅓'=0 でもある。したがってxの候補は、以下の2つ
0 ≦ ⅓ → ⅓'
⅓'≦ ⅓ → ⅓'
だが、このうちの大きい方がa→bの値、つまり ⅓ → ⅓' の値であるので等号が成り立ち、 ⅓'=⅓ → ⅓' となる。
⅓' と ⅓ についても同じことが成り立つので、以下となる。
⅓' → ⅓ = ⅓
そして当段の本題である ¬ ⅓ の定義については以下。
5値モデルで◇の左右に配されている ⅓ と ⅓' の下限(◇の下端)は 0 であるため、⅓ ∧ ⅓'=0が成り立つことが明らかだが、ここから直ちに ¬⅓ = ⅓' とすることはできない。というのは、⅓ の否定は、当段冒頭に示した否定の定義から
¬ ⅓ := ⅓ → 0
となるが、これは ¬ ⅓ が ⅓ → 0 という相対擬補元の定義によって定められる値と等しいことをいうものである。そして⅓ → 0 の値とは、相対擬補元の定義から ⅓ ∧x≦ 0 を満たす最大のxのことであり、いま、⅓' がその最大のxであるかは ⅓ ∧ ⅓'=0 だけからは決定できないからである。ここもハイティング代数定義①式を使って以下のように考える。
定義① (a∧x)≦b ←→ x≦a→b
aに⅓、xに⅓'、bに0を代入すると、
(⅓ ∧⅓' )≦0 ←→ ⅓' ≦ ⅓ → 0 ――A
いま ⅓ ∧ ⅓' =0 が成り立っていることは分かっているので、上式の第1式で等号が成立することになるが、第2式でも等号が成立するかはこれも調べてみなければ分からない。双条件の関係にある2つの不等式の一方で等号が成り立てば、他方の式でも等号が成り立つとは言えないからである。(例:a≦2 ⇔ a+b≦5 が成り立っているとして、a=2、b=2とすると、a=2 だが、それによってa+b=5とはならない。)もし成り立つのであれば、ここで直ちに ⅓' = ⅓ → 0 としてよいのだが。
すでに見てきたように、⅓ に∧演算を行って0になる∧の相方は、⅓'だけではなく0もある。すなわち、
(⅓ ∧ 0)≦0 ←→ 0≦ ⅓ → 0 ――B
も定義①式として成り立っている。A式、B式のxを比べると5値モデルの形により(定義により)0 < ⅓' であるからA式のxが大きいので、a→bの値として採用されるのは ⅓' である。すなわち ⅓' ≦ ⅓ → 0 改め、
⅓' = ⅓ → 0
である。この式はハイティング代数の擬補元 ¬ の定義の形、 ¬⅓ = ⅓ → 0 の形なので、⅓' =¬⅓ が言える。これが「例外もあります」と言われていた ⅓ と ⅓' についての理解となる。
今回、上に赤字で示した誤りに気がついたのは、当該WEB記事の⅓ → ⅓'=0 と、これに導かれて⅓ → 0 =0 として設定した5値モデル真理表(後掲)が、ある定理式についておかしな結果を示したことによる。
さて、注[22][23]で参照した『論理体系と代数モデル』では、直観主義論理の否定の性質が次のように書かれている。
「ハイティング代数ではx∧¬x=0はつねに成り立つが、x∨¬x=1は一般には成り立たない。」
また、直観主義論理の否定について、次のように伝えているWEB文献がある。
「(直観主義で)2重否定の性質とド・モルガン律が成立するような否定を定義することは可能で,これは古典論的否定あるいは擬否定と呼ばれる.しかし,この擬否定の決め方は一意ではない。」
ここからは、直観主義論理における否定というのはx∧¬x=0が満たされることが唯一の条件であり、それを満たす複数の定義が可能であって、一般にハイティング代数の否定の定義として書かれている¬x:=x→ 0は、そのような否定の決め方の一つであり、これとは別に「擬否定」という、二重否定除去則やド・モルガン律(2)aを成立させるような古典論理的な否定の定義もあるということが推察される。
ここで言われている「古典論的否定あるいは擬否定」というのは、先に「ブール代数的否定」として理解してきたものを指すように思われ、そうであればその存在は確認してきたところである。
すでに(5)の段で「ブール代数はハイティング代数の一種なので、ハイティング代数に補元がある場合もある」と理解してきたところであり、5値ハイティング代数でのように、ハイティング代数的否定と、ブール代数的否定が同時に存在してもおかしなことではないということは納得できる。
確かにどのモデルの擬補元もx∧¬x=0が果たされている。多くの場合で¬xが0だからである。そして見てきたように、5値モデルでは ⅓ と ⅓' の下限が0なので ⅓∧⅓'=0である。
なお、6値モデルの ½∧½' では、両者の下限が¼になっているので、5値モデルの⅓と⅓'とは異なり、この½と½'は相互否定の関係にはない。6値モデルでは¬½=0,¬½'=0であって、これはハイティング代数の擬補元の定義による否定である。
先の誤りが見つかった当該WEB文献では、6値モデルでは (½ → ¼)= ½' と計算されている。単純にハイティング代数3値モデルで通用する → の定義を直接当てはめるなら ½ → ¼ はa>bのパターンであるからa→b≦b、つまり ¼ となるが、これは私が上の5値モデルで犯していた誤りなので同じ轍は踏まない。
ここも6値モデルを思い浮かべて確認すると、a=½、b=¼ の場合、½ ∧x≦ ¼ となるxは ¼ と ½'。大きいのは ½' なので、(½ → ¼)= ½'であり、WEB文献の値で正しい。
なお、 ½ → ¼ のようにa>bである場合は (a∧x)≦bではなく (a∧x)=bが成立することが、前段の「3値ハイティング代数表(3)」で確認できるが(濃い青色のセル)、5値モデル、6値モデルでも同様かは確認していない。
ついでに「x∨¬x=1は一般には成り立たない」について確認しておくと、
3値モデル 元½ 擬補元0 ½∨0=½
5値モデル 元⅓ 擬補元⅓' ⅓∨⅓'=⅔
(⅓∨⅓'=⅓ではなく、∨は上限を求める計算。)
6値モデル 元½ 擬補元½' ½∨½'=¾
(½+½=1ではなく、∨は上限を求める計算。)
等々で、いずれも1にならないことが見てとれる。
これまで古典論理の「排中律」について「肯定と否定を合わせると全体を満たす」という言い方を何度かしてきたが、これら直観主義論理の擬補元では、もとの元と合せても1に満たないことが排中律の非成立を示している。ただ1と0の関係においてのみ例外的に排中律が成立しているのである。
したがって『論理体系と代数モデル』の先の文言が述べているのは、ハイティング代数は、否定に関して排中律は満たさなくてよいが矛盾律は満たさなければならないということである。
(14) クリプキ系証明表とハイティング代数モデル、否定概念のまとめ <↑> <↓>
当稿で作成したクリプキ系証明表をハイティング代数モデルと比較して、現時点での評価を与えておきたい。また、「Ⅰ型証明表が直観主義論理の非定理式を妥当式として表示する」件、および「意味論を真理表で表すことはできない」とされていることについての最終的なまとめを記す。
まず、ハイティング代数 {0, ½ ,1} の真理表はⅠ型証明表と同じであることを確認する。
Ⅰ型証明表はクリプキ意味論に基づいて16行からスタートしたが、「証明済」が「不証明」に変わる認識史はないということから9行に収まった(Hard study 5-5-1)。これにより11、10、01、00の4通りの認識史のうち10が除かれたので、命題A、Bそれぞれは3通りの認識史を持つこととなり、(3認識史)^(2命題)=9行となったのである。
一方、3値ハイティング代数の2命題真理表を作成すると(3値)^(2命題)でやはり9行となってⅠ型証明表と同じになる。
次にⅠ型証明表の証明値と3値ハイティング代数の真理値を確認してみると、Ⅰ型証明表の認識史11、01、00を3値ハイティング代数の1、½、0とみなしてよいことが分かる。
以下は、∧(下限の定義)、∨(上限の定義)、→(ハイティング代数定義)、¬(擬補元の定義)から計算した3値ハイティング代数の真理表である。
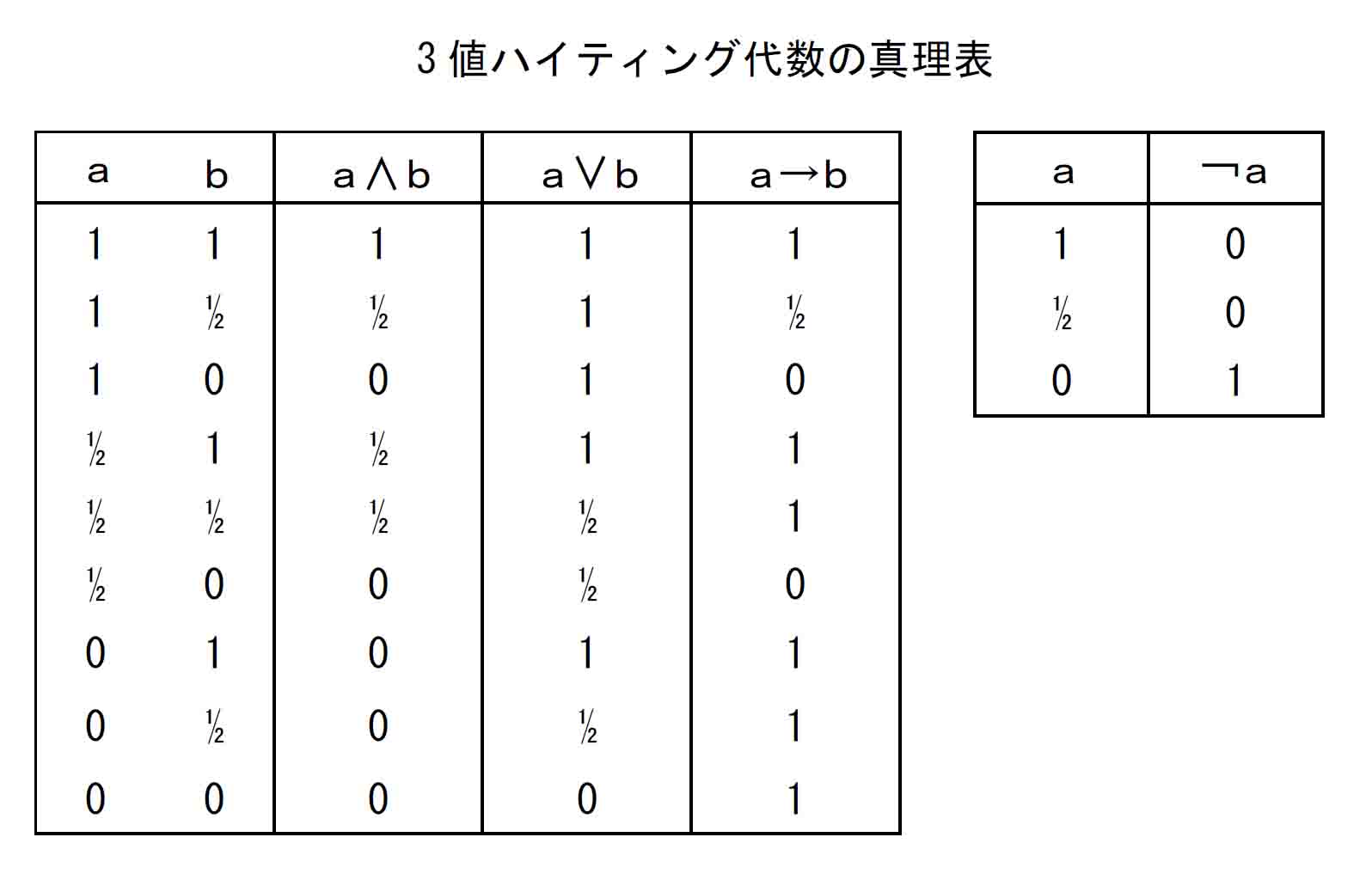
3値ハイティング代数真理表の真理値は、Hard study 5-5-1に示したⅠ型基本証明表の証明値との完全な一致がある。したがって認識史11、01、00は、それぞれ1、½、0相当である。
Ⅰ型証明表と3値ハイティング代数の値が一致するということは、それらの証明可能範囲も同じであることを意味している。
したがって、Hard study 5-5-2~3で扱ったプレ線型性 (A⊃B)∨(B⊃A) と、ド・モルガン律(2)a ¬(A∧B)⊃(¬A∨¬B)は、3値ハイティング代数モデルでも非妥当性を示すことができない。ハイティング代数モデルを掲載している先のWEB文献で、プレ線型性とド・モルガン律(2)a の非妥当性を示すための計算を5値モデルで行っているのはそのためである。
次に、否定の種類について見てみると、Ⅰ型基本証明表では認識史01と認識史00の2種の否定があるのに対し、3値モデルでは先に見たようにブール代数的否定とハイティング代数定義による否定というやはり2種の否定があり両者は一致している。(認識史01がハイティング代数定義による否定相当、認識史00がブール代数的否定相当)
以上のことから、Ⅰ型証明表と3値ハイティング代数は完全に同じであるという見方ができる。
ではⅡ型証明表と5値ハイティング代数についてはどうだろうか。確かなことは言えないが、否定の種類に関しては両者に類似があるということは言えそうである。すでにWEB掲載を取り下げたHard study 5-5-3から再録すると、Ⅱ型証明表には
1. 認識史01での├/p 直観主義論理の「やがて証明されることになる未証明」
2. 認識史00での├/t 古典論理的「否定」
3. 認識史00での├/p 三値論理的「永遠の真偽不明」
の3種の否定が設定されている。これらは5値ハイティング代数の
1. 擬補元 ¬x:=x→ 0
2. ブール代数的否定 ¬1=0、¬0=1
3. 5値モデル的否定 ¬⅓=⅓'、¬⅓'=⅓
に相当すると言えなくはない。ただし、否定の性質というよりは3種類という数に一致があるように思われて、それが当節冒頭に述べたように、一時的とはいえⅡ型証明表を生き返らせることとなった。
Ⅱ型証明表はⅠ型4値証明表とも言うべきもので、Ⅰ型では捉えられない直観主義論理の¬のふるまいを捉えようとして偽相当の認識史をⅠ型の2行から3行に増やして作成したものだが、やはりⅠ型の限界を背負っている。直観主義論理の非定理式に対して幅広く機能するものではないことが次第に明らかになってきたため、WEB掲載の取りやめに至った。
代わりに、5値ハイティング代数真理表と、それを用いたド・モルガン律9(2)a、プレ線型性の真理表を掲げておく。これらの真理値はすべて上に確認してきた計算方法によって算出されている。二つの論理式の非定理であることは見ての通りである。(ハイティング代数では1が真、1以外の値は偽。)

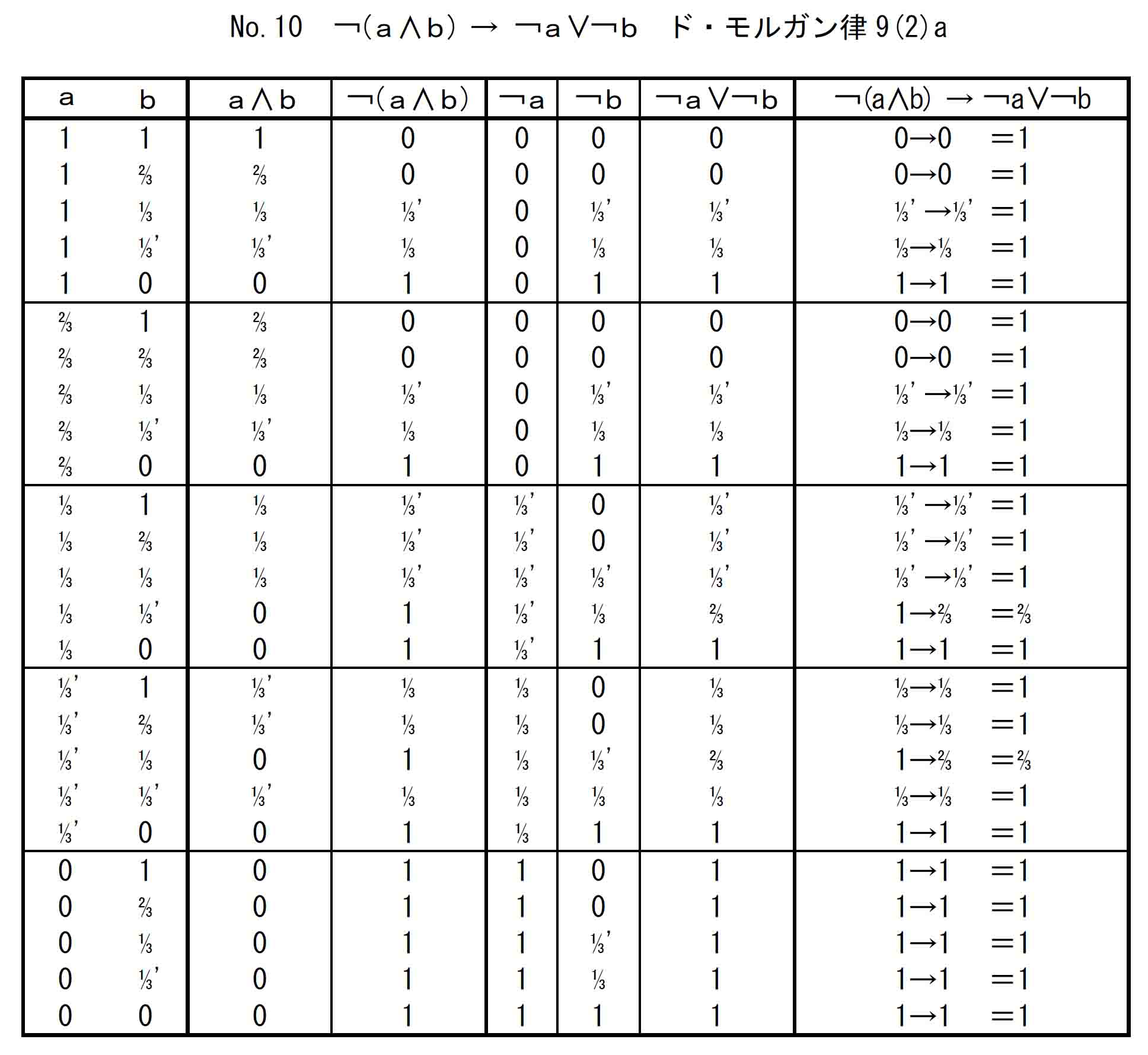
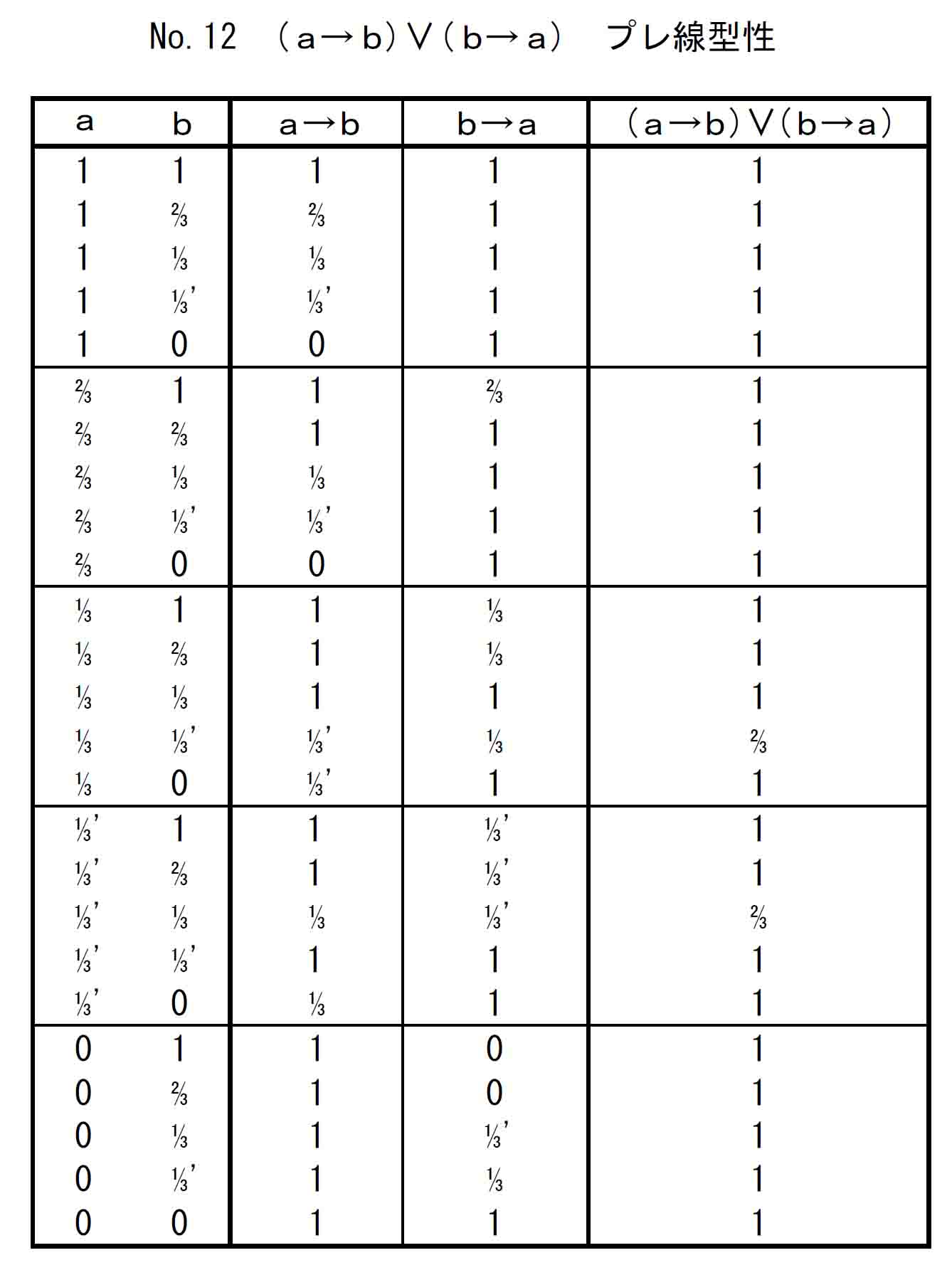
上の2式の他、「Hard study 5-5-1 クリプキ系Ⅰ型証明表」で扱った論理式12個を含む論理式21個について、「5値ハイティング代数真理表」がその妥当/非妥当を正しく表示することを確認した。
さて、クリプキ系Ⅰ型証明表、あるいは3値ハイティング代数真理表では捉えられないド・モルガン律9(2)a などの非定理性を、5値ハイティング代数真理表が正しく非定理として表示することからは「では、クリプキ系Ⅰ型証明表や3値ハイティング代数真理表をどう理解すべきなのか」という疑問が生じる。
ここで、「完全性」と「健全性」を以下のように定めると、上に見てきた限りでは、クリプキ系Ⅰ型証明表と3値ハイティング代数真理表は「不完全」であるが「健全」という評価となる。
完 全 直観主義論理で非定理である全ての式について非妥当式として表示する。
不完全 直観主義論理で非定理である一部の式について妥当式として表示する。非定理式を見逃すことがある。
健 全 直観主義論理で定理である式は必ず妥当式として表示する。
不健全 直観主義論理で定理である式を非妥当式として表示することがある。定理式を見逃すことがある。
クリプキ系Ⅰ型証明表と3値ハイティング代数真理表が「不完全」であることは、既述の通り、そのことがⅡ型証明表の作成やハイティング代数を学ぶきっかけとなったのであり、これらの「不完全」であることは確定としてよい。一方、「健全」であることについては、直観主義論理で定理である式に関して、これまで、これらのシステムですべて妥当として表示されてきたことによる見通しである。
クリプキ系証明表とハイティング代数3値モデルが、直観主義論理に対して「不完全」であることについての、現行の私の理解は以下のようである。
古典論理の一般式、例えばA⊃Bの真理表を思い起こしてみると、真理表の4行すべての真理値が1となるとき、この論理式のトートロジーであることが示される。しかしA⊃Bの真理表は2行目が0であり、トートロジーではないことがこの2行目によって示されている。
つまり古典論理において、論理式が非定理であることは真理表の4行中の1行が偽を示すことを確認することで確定する。逆に、それが定理であることは、真理表の4行全てが真を示していることを確認しなければならない。
これと同じように、クリプキ系証明表とハイティング代数3値モデルが直観主義論理意味論から正しく作られたものである限り、それによって非妥当として示された論理式は直観主義論理において非定理であることが確定する。非定理の確定のためには、あらゆるクリプキ系証明表、あらゆるハイティング代数モデルの中で、1つだけ非定理を示す行があればそれで充分だからである。
そして同じく、クリプキ系証明表とハイティング代数3値モデルが妥当として表示する論理式については、それによってその式を直観主義論理において定理であると確定することはできない。定理であることをこれらのモデルによって確認するためには、古典論理のトートロジーにおいて真理表の全行が1でなければならないのと同様に、直観主義論理のすべての意味論モデルが⊩で埋め尽くされることを確認しなければならないからである。
つまり、ある論理式をⅠ型証明表とハイティング代数3値モデルが定理として表示する事態とは、古典論理に例えれば「真理表4行の一部の行しか見ることができない状況」だと理解するのが正しいということである。
したがって、クリプキ系証明表とハイティング代数3値モデルは「不完全」ではあるが、非定理を示すための有効なモデルであり「健全」である。これらのモデルを直観主義論理意味論の一員とは見ずに、それをもって全員と見なすとき、非定理である論理式の一部を妥当式として表示することが誤った表示と見えるのである。
この事態は当然ながらハイティング代数5値モデルにも当てはまることであるだろう。5値モデルが特別である理由はなく、これまでに調べてきた21個の式については「完全」を示してきたということであるにすぎない。5値モデルも直観主義論理意味論の一員という立場である以上、やはりそれは「健全」ではあるが「不完全」である。
そこで、Hard study 5-2-4 以来、懸案となってきた「直観主義論理意味論を真理表で表すことはできない」という野矢茂樹『論理学』に書かれていた意味深な文言を、どう理解すべきなのかも見えてきたとしてよいだろう。
これまでに見てきた通り、直観主義論理の意味論を証明表や真理表で表すことはできる。ただし、どのモデルもそれ一つでは完全ではない。どのくらいのモデルが揃えばよいのか、というとおそらく無限に必要ということになるのだろう。5値モデルでは古典論理で定理でありながら直観主義論理では非定理である式のかなりの部分が賄えることが分かったが全部の式を賄えるわけではない。
したがって、「直観主義論理意味論を真理表で表すことはできない」というのは、「真理表で表すことはできるが完全にはできない。なぜならその類いの真理表を無限に必要とするからだ」ということになる。この意味で『論理学』の文言は誤りではない。しかし不親切というか、混乱を与えるのに十分な記述であるということは言っても許されるだろう。
否定に関するクリプキ系証明表とハイティング代数モデル真理表を並べて、いくつかのことを考察したい。



直観主義論理には三重否定除去則という定理があり¬¬¬A⊃¬Aが成り立つ。
Hard study 5-4-2に「直観主義論理¬には『否』と『不』の二義が含まれる」と述べた。こちらは¬そのものに二重性があるという見方である。これらの見方は整合するのだろうか。
上の三つの真理表を見ると、¬¬¬A⊃¬Aが成り立つ様子がよく分かる。どの真理表においても¬¬¬Aと¬Aの真理値が同じであることで¬¬¬A⊃¬Aが成立していることが一目瞭然であるのはもちろんのこと、¬A以降(以右)の証明値パターンが証明値の反転を繰り返していることが明らかで、新しい証明値パターンが現れないことを示しているからである。
つまり、¬¬¬A⊃¬Aが成り立っているのは、¬¬Aに新たに加わった¬が相殺を起こしているというのではなく、第1にAから¬Aへの証明値の変換があり、第2に¬Aから¬¬Aへの証明値の変換があって、以降は第2の変換の繰り返しがあることで、¬¬¬Aがそれ以上¬を有意味に増やすことがない状況が現出しているということである。
この状況をまとめると、直観主義論理の否定には、まず、第1の証明値変換としてAから¬Aへの変換がある。これは、ハイティング代数3値モデルでは1から0、0から1、½から0という、古典論理とは異なるイレギュラーな証明値変換である(Ⅰ型証明表、5値モデルも同様)。そして、第2の証明値変換として、¬Aから¬¬Aへの変換があり、これは1から0、0から1、⅓ から ⅓'、⅓'から ⅓ への証明値変換であり、証明値の反転という意味で古典論理の否定と同じ変換である。
したがって、¬¬¬A⊃¬Aが成り立つことで、¬が実質的にこれ以上は増えないのは¬による相殺によるというのではなく、一度、直観主義論理独特の否定変換が行われた後、それ以降は古典論理と同じ証明値反転を繰り返すことで、否定の証明値パターンが増えないことによる、と理解するのが正しい。
ただし、古典論理の二重否定除去を¬Aに対する¬の相殺(Hard study 5-4-2 後半部参照)によると見てよいのであれば、直観主義論理の三重否定除去を¬¬Aに対する¬の相殺と見ることも誤りではないだろう。直観主義論理は、¬に関しては一つの否定が入った後は古典論理と同じふるまいをするといえるからである。
Hard study 5-4-2に書いた「直観主義論理¬の二義性」という見方についてはどうだろうか。WEB掲載を取り下げたHard study 5-5-3のⅡ型証明表では¬を三重性を持つものと見ていたのだった。
この「¬の二義性」「三重性」という捉え方が適切であったことについては上の真理表から見てとれる。
Ⅰ型証明表での¬A、すなわちAからの第1の証明値変換は、Aの認識史01(α⊮、~β⊩)の否定と、Aの認識史11および00の証明値の反転による古典論理的な否定の二義を持っている。ハイティング代数3値モデルも同じである。
ハイティング代数5値モデルの¬A(第1の証明値変換)では、それらに加えて、証明値の反転という点では上の古典論理的否定と同じでありながら、⅓と⅓'という下限は0だが上限は0ではない、つまり否定を繰り返すと0と1の反転になるのではない証明値の反転パターンがある。つまりハイティング代数5値モデルの¬は三重の振る舞いを内包しているのである。
Hard study 5-4-2では¬の二義性を「不」と「否」として表現した。前者が認識史01相当で「肯定の未証明」、後者は認識史00相当で「否定の証明」である。そして、Hard study 5-5-1に掲載した意味論規則
(ハ) Ⅱ(5)←方向(証明済の¬の導入則)
すべてのβで⊮Aのときαで⊩¬A
すべての期で命題Aの肯定が証明されない場合、頭初期で否定が証明されている
により、最後まで不証明が続く事態を否定の証明と同等と見なすのであった。
ただし、これは認識史が有限である場合に言えることであり、無限の期を考えると「最後まで不証明が続くのを見届ける」ことはできないので(Easy Study 5-1)、限られた期の不証明をもって否定の証明と見なすことはできないと考えられなければならない。つまり、クリプキ意味論そのものは「永遠の不証明」という事態を含意していると考えられるのであり、ただしそれはⅠ型証明表のような有限期での証明表によって表すことはできないということである。
この点を勘案すると、5値モデルでの⅓と⅓'に、クリプキ系Ⅱ型証明表での「永遠の真偽不明」としての否定を対応させるという、先の見方も的を外したものではないといえる。
直観主義論理の擬補元 ¬ の値は、すべて相対擬補元 → の定義から導かれているが、5値モデルでのAから¬Aへの第1の証明値変換に注目すると、
⅔から0、1から0、0から1
という相対擬補元による¬の定義に基づく変換と、
1から0、0から1、⅓から⅓'
という古典論理的な証明値反転による変換がある。両者に共通する
1から0、0から1
を古典論理の変換として別に取り出すと、ここに見てきた直観主義論理では、¬ の種類として3通りがあると見ることができる。直観主義論理の否定概念をこの分類によってまとめておく。
¬の複数定義まとめ
ここまでの考察において3種類の¬の定義を認めることができる。¬が3種類に分類されることは、それぞれの¬の働き方において論理式の妥当/非妥当の弁別に違いが出るためである。
相対擬補元 → において前件xと後件yに順序関係がある場合の¬xは以下。
x≦ 0のとき、すなわちx=0のとき、x→ 0=1 すなわち¬x=1
x>0のとき、すなわちxが0以上のとき、x→ 0=0 すなわち¬x=0
この定義による¬xは、x,yのいずれかが0である¬xであり、以下の2種類。
¬xの種類1:x∧y=0 かつ
x∨y=1 となるy(ブール代数の補元の定義と同じ¬の定義)
例:3値ハイティング代数 x=0のときのy(y=1)
x=1のときのy(y=0)
5値ハイティング代数 x=0のときのy(y=1)
x=1のときのy(y=0)
クリプキ系¬の証明表認識史11、認識史00
種類1の¬xは古典論理の補元と同じ。
¬xの種類2:x∧y=0 ただし、yすなわち¬xが0で、かつ
x∨y<1 となるy
例:3値ハイティング代数 x=½のときのy(y=0)
5値ハイティング代数 x=⅔のときのy(y=0)
クリプキ系¬の証明表認識史01
種類1の古典論理の¬xに、種類2の¬xが加わることで排中律、二重否定除去則などの非定理を示すことができるようになる。
ただし種類2の¬xでは、例えば、3値ハイティング代数x=½のとき、¬x=0、¬¬x=1 であり、種類1と同じく二重否定でのxの値が1となる。つまり、x∨¬x<1 だが、¬x∨¬¬x=1 であり、直観主義論理の非定理式¬x∨¬¬xが「定理表現」となる。
3種類目の¬xは、 → の前件xと後件yに順序関係がなく、また、x,yのいずれも0ではないが、x,yの下限は0である¬x。
¬xの種類3:x∧y=0 ただし、x,yのいずれも0ではなく、かつ
x∨y<1 となるy
例:5値ハイティング代数 x=⅓のときのy(y=⅓')
種類1、種類2の¬xに種類3の¬xが加わることで、ド・モルガン律9(2)a、プレ線型性、¬A∨¬¬Aの非定理を示すことができるようになる。
種類3の¬xでは、例えば、5値ハイティング代数x=⅓のとき、¬x=⅓'、¬¬x=⅓ のように二重否定でのxの値が1にならないことが種類2との違い。したがって、x∨¬x<1 で、¬x∨¬¬x<1 である。
排中律のように、古典論理で定理、直観主義論理で非定理となる論理式は、何によってそれが非定理となっているのかという性質が古典論理の非定理式、例えばA⊃Bなどの一般式とは異なる。そのため、論理式の意味を重視したい立場としては、直観主義論理での非定理式をすべてひとまとめにするのではなく、一般式として古典論理においてすでに非定理であるのか、直観主義論理における偽の複数性がもたらす非定理であるのかを区別することは重要な視点と思える。
直観主義論理において初めて非定理となる論理式は、古典論理では明らかにならない非定理性を潜在させていると見ることもできる。排中律の非定理性は、二種類の偽を設定するⅠ型証明表と3値ハイティング代数によって明らかになる。同様に、プレ線型性とド・モルガン律(2)a および ¬A∨¬¬Aに潜在する非定理性は、三種類の偽を設定するⅡ型証明表と5値ハイティング代数によって、ようやく明らかになるということである。
このことは、論理学の意味論が論理と世界の対応付けを行うものであるということを省みるとき意義深いものであるように思われる。常識的な古典論理の視点では、世界は「内在と超越」という、常に二分された世界に見えている。しかし、実は内在の否定としての超越には複数の種類の否定が存在しており、それら複数の否定を明るみに出す新たな論理を採用した視界にとっては、世界は二分された世界というものではなくなってくるということである。
250年前にカントは形而上世界に対する理性の無制約の使用を誤りとする『純粋理性批判』を発表した。現在では、形而下世界における古典論理のイデオロギー的使用が作り上げる二元世界観が正しいわけではないことが知られるべきであるだろう。
さて、この「Hard Study」は直観主義論理における否定概念の追求として始まったので(Easy Study 5-1 最後から5行目の記述)、否定概念のまとめを終えたことによってひとまず終わりを迎えた。