| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (25)
Hard study 5-5-3 ド・モルガン律のためのⅡ型証明表
頁内目次
(1) ド・モルガン律のための証明表
(2) Ⅱ型証明表の作成
(3) 偽値の演算規則
(4) Ⅱ型証明表による諸定理の表示
No.10 非定理 ¬(A∧B)⊃(¬A∨¬B) ド・モルガン律9(2)a
No.11 定理 (¬A∨¬B)⊃¬(A∧B) ド・モルガン律9(2)b
No. 8 定理 ¬(A∨B)⊃(¬A∧¬B) ド・モルガン律9(1)a
No. 9 定理 (¬A∧¬B)⊃¬(A∨B) ド・モルガン律9(1)b
No. 1 非定理 A∨¬A 排中律
No. 2 非定理 ¬¬A⊃A 二重否定除去
No. 3 非定理 (¬B⊃¬A)⊃(A⊃B) 反対偶律
No. 4 非定理 (A⊃B)⊃(¬A∨B) 古典論理条件法(1)
No. 5 定理 (¬A∨B)⊃(A⊃B) 古典論理条件法(2)
No. 6 非定理 ((A⊃B)⊃A)⊃A パース律
No. 7 非定理 A⊃(B∨¬B)
(1) ド・モルガン律のための証明表
非定理であるド・モルガン律をⅠ型証明表が正しく表示しない理由を考えたい。
Hard study 5-5-1 に見た通り、Ⅰ型証明表はド・モルガン律の非定理¬(A∧B)⊃(¬A∨¬B)および、前件、後件を入れ替えた同じくド・モルガン律の定理(¬A∨¬B)⊃¬(A∧B)を、いずれも妥当式として表示する。
このとき証明表が示す前件と後件の証明値は同じであって、それは見るからに腹立たしい。なぜかと言うに、¬(A∧B)と(¬A∨¬B)が全く同じ証明値であっては、その入れ替えによって、一つを非妥当式、もう一つを妥当式として表示するなどという芸当はとてもできそうにないからである。
仮に、ド・モルガン律(2)aを非妥当式として表現する規則を、直観主義論理の⊃記号の特異性(認識史0100)などに見い出せたとしても、その規則は、前件後件を入れ替えたド・モルガン律(2)bをも非妥当式にしてしまうだろう。なぜなら前件と後件が同じ証明値である以上、それを入れ替えたド・モルガン律(2)bは、入れ替え前の(2)aと同じ事態を再現するだけであることは明らかだからである。
しかしこのことは、Ⅰ型証明表でド・モルガン律(2)aが不正表示となる原因として考えられるべきであるのが、⊃についての意味論の捉え方や、⊃に関するⅠ型証明表の作り方ではないことを示している。
つまり問題は、¬(A∧B)と(¬A∨¬B)が同じ証明値になっている点にあると考えられるのである。ただしここに含まれる∧と∨記号については、その規則がα期に集約されることから古典論理と同じ規則といえるので、このところに誤りや何かの見落としがあるとは考えにくい。残りの¬記号の中に、問題は隠れていると予想される。
一方で、¬(A∧B)と(¬A∨¬B)が同じ事態を示すものであることは明らかであるようにも思われる。実際、これを高校数学に出るベン図のような領域図としてイメージする限り、この二つの式には何の違いも見つけられない。これらが同じ証明値であることは当然のことと思えるのである。
ただし、これまで直観主義論理の¬の意味を「不証明」と「否定」という二重性において追求してきた(Hard study 5-4-2、5-4-4)ことを思い起こすと、¬(A∧B)と(¬A∨¬B)の違いを述べることは、むしろ容易であることにも思い至る。
Hard study 5-4-2での表現を用いると、¬(A∧B)という主張は、A∧Bについて、
① 不(A∧B)であるか、または
② 否(A∧B)である
という2つの要素からなる主張を行うものである。これはド・モルガン律により、
① 不A∨不Bであるか、または
② 否A∨否Bである
と言い直すことができる。
これに対し、¬A∨¬Bという主張は、
(1) 不A∨不Bであるか、または
(2) 不A∨否Bであるか、または
(3) 否A∨不Bであるか、または
(4) 否A∨否Bである
という4つの要素からなる主張を行うものである。
①と(1)は同じ式で、②と(4)も同じ式である。そして¬A∨¬Bの(2)と(3)に対応する¬(A∧B)の要素は存在しない。
したがってベン図では同じに見える¬(A∧B)と¬A∨¬Bは、偽に関わる主張について、前者は後者よりも狭い主張であるといえる。¬A∨¬Bは¬(A∧B)を包含するが、¬(A∧B)は¬A∨¬Bを包含しない。それゆえ、ド・モルガン律(2)b ¬A∨¬B⊃¬(A∧B)は成立するが、(2)a ¬(A∧B)⊃(¬A∨¬B)は成立しないのである。
この見通しをⅠ型証明表の整合性を保ちながら証明表に反映させることができれば、ド・モルガン律(2)aと(2)bを区別する証明表ができるはずである。
そのためにはまず、¬記号を、上の(1)~(4)の「不」と「否」の組み合わせに相当する偽として多重化する。実際には(2)と(3)は前後関係が異なるだけなので、これを一種類とみなすことができるので、¬記号を三重化することを考える。その上で、①②と(1)(2)(3)(4)の領域差を表現するために、集合演算の「外部結合」を導入する。
すでにⅠ型証明表の作成で、2つの論理式が持つ認識史を一つの認識史にまとめる際に、集合演算の「直積」と「内部結合」を行っているが、ここに「外部結合」
(2) Ⅱ型証明表の作成
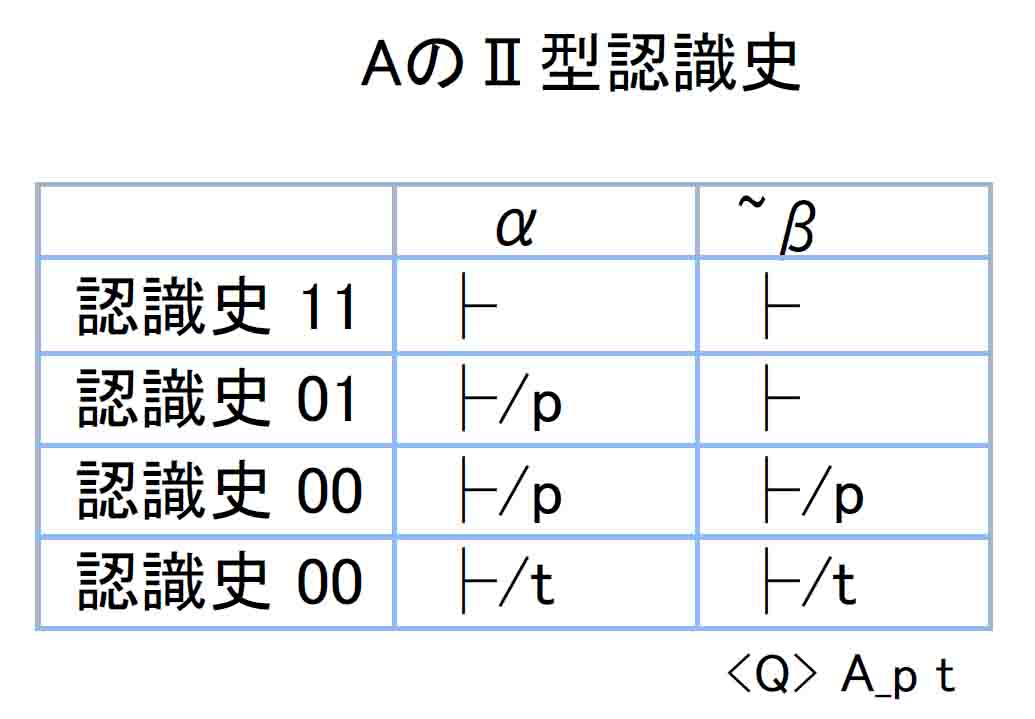
AのⅠ型認識史および、そのときの¬AのⅠ型証明表は以下。(Hard study 5-2-4 から再掲)

Ⅰ型証明表は⊩と⊮に関する演算を行うものであり、⊮自身の二重性は表さない。
直観主義論理構文論の公理(『論理学』p.167)には証明表の⊩、⊮はなく、否定記号は¬だけである。Hard study 5-4-2では、この構文論の¬に直観主義論理意味論由来の「不証明」と、古典論理由来の「否定」としての偽が二重に含まれていることを考察した。
では、直観主義論理意味論の⊮自体についてはどうだろうか。同箇所でも⊮の二重性について言及したが、もう少し詳しく見てみる。
証明表左半分の「Aの認識史」において、⊮は認識史01α、認識史00α、認識史00~βの3箇所にある。
認識史01αの⊮は将来証明されることが定まっている⊮であるので、これは「未証明」としての⊮であり、直観主義論理で導入された新たな偽の概念として理解してよい。(例えるなら、「ダークマター」が存在しているのだが能力不足により現時点でそれを認識できないという状況。)
そうすると認識史00の⊮は、¬の二重性におけるもう一方の偽である「否定」を意味するということになる。つまり、意味論は構文論の¬の二重性を認識史01と00で分けているので、このままで、偽内部の区別に由来すると考えられるド・モルガン律(2)aと(2)bの区別も表現できるはずと考えられる。
そうであるなら、これを区別できなかったⅠ型証明表は、認識史01と認識史00の扱いに関する何らかの不十分さがあるということになる。
確かにⅠ型証明表は、認識史01の⊮と認識史00の⊮に記号としての区別を設けていないので、否定の意味を考えればその点に不十分さがあると言えるのかもしれない。しかし、記号は同じでもそれらが異なる認識史に配されていることで、二つの⊮は十分に区別されていると言うこともできるだろう。ただしこの認識史01と00による区別ではド・モルガン律(2)aの非妥当性を示すことはできないということである。
そこで⊮が持ちえる意味をさらに考えてみると、認識史00の⊮がそれ自身二重の事態を内包しており、これを区別することが可能であることが分かる。
<1> 認識史00のα⊮A、~β⊮Aを、命題Aの肯定が最後まで明らかにならなかったことを示すものと見るとき、これは意味論Ⅱ(5)(ハ)に該当し、αでの⊮は「否定の証明」である。そしてこの「否定の証明」は古典論理の「偽」に相当する。(ここまで、認識史00の偽はこの意味のものとして捉えてきた。例えるなら、「ダークマター」が存在しないので認識できないという状況。)
<2> 認識史00のα⊮A、~β⊮Aを、Aであるか否かの真偽が最終期まで明らかにならなかった事態の表現と見ることもできる。その場合、これら二つの⊮は「永遠の真偽不明」を意味することとなり、三値論理の「不明」に相当するといえる。(これにより新たな偽の概念が加わる。これは認識史01の「現時点での不証明」と認識史00の「否定」が融合した概念ともいえる。例えるなら、「ダークマター」を認識できない理由が、それが存在していないからなのか、能力不足だからなのかが分からないという状況。)
ここに認識史01α⊮Aを加えると、Ⅰ型証明表の⊮は、
1. 認識史01での、直観主義論理の「やがて証明されることになる未証明」――(1)不A∨不B相当
2. 認識史00での、古典論理的「否定」――(4)否A∨否B相当
3. 認識史00での、三値論理的「永遠の真偽不明」――(2)(3)不A∨否B相当
という3種類の偽を保持するものとして理解することができる。
このようにして、認識史00の⊮を証明表で二重に表現すると、偽について三様のあり方を持つことになるが、このことは、先の「Ⅰ型証明表がド・モルガン律(2)aを正しく表示しない原因を¬の二重性に求めると、¬の二重性を⊮を認識史01と00によって区別しているⅠ型証明表がそれを表現できないことが理解できなくなる」という疑問を解決するものともなる。
つまり、Ⅰ型証明表がド・モルガン律(2)aを正しく表示しない原因は、¬の二重性にあるのではなく⊮の二重性にある可能性があるということである。すなわち、¬を認識史01と00における二重性として表現するだけの証明表ではド・モルガン律(2)aと(2)bを分離できず、認識史00における⊮の二重性を捉えた証明表でなければ分離できない、というのがここでの見通しである。
Ⅰ型証明表の結果を振り返ってみると、非定理式を非妥当式として示す⊮が表示されているのは認識史1101、0101、0100等、全て認識史01がらみの認識史においてである。これは証明表における認識史01の存在が、古典論理の定理を、直観主義論理の非定理として示すことに成功させているということである。こうして直観主義論理の公理系LIP(『論理学』p.167)の¬記号を、意味論において認識史01と00に分離したことで、直観主義論理における定理/非定理の識別がとりあえずは可能になったといえる。
しかしそれにも拘わらず、Ⅰ型証明表がド・モルガン律(2)aの非定理性を表示できないということは、¬を認識史01と00に分離するだけでは不十分だということである。そこで、本来の(古典論理由来の)¬である認識史00はさらにそれ自身が分離されなければならないということなのである。
したがって構文論の¬については二重性ではなく三重性があるという見方となる。この見方の上に、先に述べた¬(A∧B)と¬A∨¬Bの領域差を表現するための「外部結合」を導入することで、ド・モルガン律(2)aの非定理性を示す証明表ができるだろう。
この「外部結合」は、これによって¬(A∧B)と¬A∨¬Bの違いを捻出するというものではなく、あくまでもその違いを目に見える形にするための手法にすぎない。¬(A∧B)と¬A∨¬Bの違いは認識史00における⊮の二重性がもたらすものである。そこで以下のように考える。
⊮を、「証明/不証明」に関する偽⊮ proof(⊮ p)と、「真/偽」に関する偽⊮ truth(⊮ t)に分ける。
三値論理的「真偽不明」の偽は、その意味から「証明/不証明」に関する偽(⊮ p)に割り当てる。
そこでAの認識史は以下のようになる。この表記を持つ証明表を「Ⅱ型証明表」と呼ぶ。
Ⅱ型証明表では、演算にMicrosoft Access®を使用する関係で、証明記号をこれまでのものから置き換えて
⊩ ⇨ ├
⊮ ⇨ ├/
⊮ p ⇨ ├/p
⊮ t ⇨ ├/t
で表示する。
Ⅱ型証明表のタイトル横または表下に記載の<Q>は、データ提供予定のAccessクエリの略記、<Mcr>は同マクロの略記で、これに続く文字列はクエリ、マクロの名称。ただし、以下のⅡ型証明表は紙上(画面上)で演算を確認できるようにしているので、Accessデータの参照は必須ではない。

偽値の認識史についての注:
├/pを「不値」、├/tを「否値」と呼び、両方をまとめて「偽値」または「不否値」または「pt値」と呼ぶ。
Aの認識史00がα├/p、~β├/tであることはない。~βで否定が確定しているとすれば、αでの├/は否定の意味の├/である。この場合、認識史00はα├/t、~β├/tと解さなければならない。直観主義論理においては、未来の最終的な状態が現在の状態を確定させるのである(Hard study 5-2-2)。
Aの認識史00がα├/t、~β├/pであることもない。αで否定として定まっているものが将来において不証明や真偽不明に転じることはない。逆に、将来においてなお不明であるものは、その当初においても不明だったのである。したがってこの場合はα├/p、~β├/pであるか、または初めに否定が定まっていてα├/t、~β├/tでなければならない。
偽値が├/pでありかつ├/tであることはない。直観主義論理の偽は二重性を持つが、それは不証明か否定のいずれかである二重性であり、両者が同時に存在する二重性ではない。この点は Hard study 5-4-2の当該箇所 に述べた。偽値が排反的に├/pであるかまたは├/tであるという意味での二重性を持って存在することは可能である。
偽値同士の演算規則を次のように設定する。
(3) 偽値の演算規則
論理式に¬が出てくるまではⅠ型証明表で演算を行う。¬が付いたⅠ型証明表になった時点で、それをⅡ型証明表に移行する。移行の規則は「(5)¬演算」を参照。A∨¬Aのように、最初の段階から¬が出てくる論理式では、¬のない命題記号(この場合はA)についてもⅡ型認識史またはⅡ型証明表を用いる。
(1) 偽値演算は偽値同士においてだけ定められる。├/pと├/tは、├に対しては├/としてふるまい、Ⅰ型証明表と同じ演算を行う。
(2) ∧演算
├/p ∧├/p → ├/pp
├/t ∧├/t → ├/tt
├/p ∧├/t → ├/ptとなるので、偽値注によりこの認識史は除外される。
∧演算は├/ptを生成しない。
├/t ∧├/p → ├/tp 上と同じくこの認識史は除外される。
(3) ∨演算
├/p ∨├/p → ├/pp
├/t ∨├/t → ├/tt
├/p ∨├/t → ├/pt
この├/ptは∨演算によるものなので、├/pまたは├/tであるものとして成立可能。∨は非排反的選言なので├/pでありかつ├/tの状態が可能だが、偽値として生成される├/ptには両立の状態はない。Hard study 5-4-2(「水」∨「石」は真とは、それが「水」または「石」であるか、その両者であることを主張するものだが、実際には「水」であり「石」でもあることを主張していないのと同様)
├/t ∨├/p → ├/tp 上と同じく成立可能。
(4) ⊃演算
1. ⊃記号の前件と後件の証明値において、すべての期が偽値である認識史があり、かつ、そのうちの一方に存在する偽値が他方のどの認識史にも含まれていない場合(例えば、一方の論理式の認識史1111に├/ptがあるが、他方にはいずれの認識史にも├/ptが存在しないという場合)は、3.の演算に進む。その状況がなければ 2.に進む。
2. A、Bを論理式、xをp, t, pt, tp のいずれかとして、同期同士を以下のように演算して終わる。
(1) ├A ⊃├B → ├A⊃B
(2) ├A ⊃├/xB → ├/xA⊃B
(3) ├/xA ⊃ ├B → ├A⊃B
(4) ├/xA ⊃ ├/xB → ├A⊃B
(4)において、~β├A、~β├/xBがあるときはαで以下とする。
α├/x1A ⊃ α├/x2B → α├/x2A⊃B
前件と後件が異なる偽値の場合、例えば├/p ⊃├/tの場合、├/p ⊃├/tを「├/pではないまたは├/tである」と解して、偽値内で「├/pではない」とは「├/tである」ことなので、├/p ⊃├/tは「├/tであるまたは├/tである」の意味になるので├/tとする。├/t ⊃├/pも同様。
3. 認識史行を├を含む行と含まない行に分ける。
├├/演算と偽値同士の演算は通常は同時に行うが、1.からの分岐によってここでの偽値同士の⊃演算が発生する場合は、規定の⊃演算の前に⊃の前件と後件の包含関係を明らかにするための外部結合を行う。
このとき、AB2命題での通常の├├/演算が認識史同士を内部結合するのに対し、偽値同士の⊃演算では、認識史同士に加えて期同士の外部結合を行うため、これをコンピュータ上で行う場合は、証明表を├を含む行と含まない行に分けて、それぞれの演算処理を行うことが必要となる。次段の「(4) Ⅱ型証明表による諸定理の表示」でのⅡ型証明表の表示はこの流れに沿っている。
3a.├を含む認識史行では2.の処理を行う。
3b.├を含まない認識史行は偽値の種類の多い側からの外部結合を行う。(外部結合の方向は⊃の前件後件とは無関係)。結合項目は認識史、α期、~β期。2命題論理式では認識史は2つあるので、計4項目の結合となる。
├を含まない認識史行で以下の偽値演算を行う。
├/x ⊃ 空値 → ├
空値 ⊃├/x → △「未定義」を示す記号
├/x ⊃├/x → ├
(5) ¬演算
証明表をⅠ型からⅡ型に移行するとき、├/を含む認識史に以下のように不否値を設定する。
α├/、~β├ は、α├/p、~β├ とする。
α├/、~β├/は、α├/p、~β├/p
α├/t、~β├/t と2行化する。
論理式にさらに¬が付加されたときは、それまでの不否値を捨て、改めて上の仕方で不否値を設定する。
(6) 不否値二重記号
∧演算から得られる├/ppと、∨演算から得られる├/ppは、その意味により同等であり同記号とする。├/ttについても同様。
また、
├/p ⇔ ├/pp 意味から考えて両者は同等なので互換可とする。
├/t ⇔ ├/tt 同上
(4) Ⅱ型証明表による諸定理の表示
以上の偽値演算規則に基づいて、ド・モルガン律(2)aのⅡ型証明表を作成する。
その後、ド・モルガン律(2)a以外の論理式の妥当/非妥当を正しく表示するかについても確認する。
■No.10 非定理 ¬(A∧B)⊃(¬A∨¬B) ド・モルガン律(2)a
前件¬(A∧B)のⅠ型証明表は以下。
_ProofMatrix.jpg)
<Q>¬(A∧B)pre∑
Ⅱ型証明表への移行。
Ⅱ型証明表では、偽値演算規則(5)によって¬(A∧B)の証明値にpt値が付加される。
α├/、~β├/である認識史1111、1101、0111、0101では認識史が2行化される。
_.jpg)
¬A∨¬Bとの照合のため、偽値演算規則(6)によって¬(A∧B)のpt値を2桁にする。
∨¬(A∧B)_.jpg)
¬A∨¬Bのpt証明表では¬A、¬Bに¬があるので、この段階からpt値が付加される。認識史11、認識史01がα├/、~β├/のため2行化される。


¬A5行、¬B5行の認識史から集合演算直積により¬A、¬Bの認識史25行を得る。

偽値演算規則(3)によって¬A∨¬Bの証明表を作成。

¬(A∧B)と¬A∨¬Bの偽値の状況を調べる。
¬(A∧B)で偽値だけの認識史行は以下。¬A∨¬Bで偽値だけの認識史行は以下。
pp.jpg)

両者に、α、~βが共に偽値である認識史行があり、¬A∨¬Bには¬(A∧B)には存在しない├/pt、├/tpがあるので、偽値演算規則(4)の3に従って、¬A∨¬B → ¬(A∧B)方向の外部結合を行い、同時に⊃演算を行う。
⊃¬A∨¬B.jpg)
¬(A∧B)⊃(¬A∨¬B)のⅡ型証明表は、¬(A∧B)のとき¬A∨¬Bが必ずしも成り立たないことを示している。
ここで空値を意味する△は、├/p、├/t、├/pt(├/tp)に次ぐ第四の偽値のようにも見える。この△は¬A∨¬Bに、¬(A∧B)には存在しない├/pt、├/tp という、認識史01と認識史00が融合した偽値があることを示している。
したがって、ここで見る偽の概念としては、
不証明(やがて証明されるはずの未証明)
否定 (証明された偽)
不明 (永遠の真偽不明)
無知 (存在そのものが知られていない)
があることになる。
¬(A∧B)は、¬A∨¬Bの├/ptや├/tpを知らないので、¬(A∧B)⊃(¬A∨¬B)であるとは言えないのである。
■No.11 定理 (¬A∨¬B)⊃¬(A∧B) ド・モルガン律9(2)b
No.10の前件、後件を入れ替えた式。
No.10の最終表の列を入れ替えて、偽値演算規則(4)の3bにより下の証明表を得る。
_.jpg)
■No.8 定理 ¬(A∨B)⊃(¬A∧¬B) ド・モルガン律(1)a
No.10、No.11の結果からは、Ⅱ型証明表がNo.10 ¬(A∧B)⊃(¬A∨¬B)を非妥当式として表示するのは、単に、⊃前件の¬の数が後件よりも少ないからではないかという見方が生じるかもしれない。
しかし、同様の事態にあるNo.8 ¬(A∨B)⊃(¬A∧¬B)のⅡ型証明表をみると、そういうことではなさそうだということが分かる。No.8は前件の¬が後件より少ないが、Ⅱ型証明表はこれを妥当式として表示する。
まず、前件¬(A∨B)のⅠ型証明表を Hard study 5-5-1 から再掲する。
_ProofMatrix.jpg)
偽値演算規則(5)を適用してⅡ型証明表を作成する。認識史0000以外の全ての認識史が2行化される。
偽値演算規則(6)によりpt値を2桁にする。
_.jpg)
¬A∧¬BのⅡ型証明表を、前出¬A、¬Bの認識史を使って作成する。
偽値演算規則(2)により、├/pt、├/tpとなる認識史行は除外される。

¬A∧¬Bのpt値を2桁化し、¬(A∨B)と¬A∧¬Bの同認識史と同期を外部結合する。結合方向は、¬(A∨B)と¬A∧¬Bの一方にしか存在しない偽値がないので、どちらからでもよい。
⊃(¬A∧¬B)_.jpg)
■No.9 定理 (¬A∧¬B)⊃¬(A∨B) ド・モルガン律(1)b No.8の逆
No.8のⅡ型証明表で¬(A∨B)と¬A∧¬Bの証明値は同じなので、前件後件を入れ替えたNo.9が妥当式として表示されることは明らか。
以下、Ⅰ型証明表で正しく表示されていた残り7個の式(プレ線型性以外)について、Ⅱ型証明表が正しく表示することを確認する。
■No.1 非定理 A∨¬A 排中律

認識史01で2種類の├/を確認できる。
■No.2 非定理 ¬¬A⊃A 二重否定除去則
偽値演算規則(5)により偽値は¬によって一新されるので、¬Aのpt値は一旦捨てられて通常の├/に戻される。

¬¬Aに不否値を設定する。AのⅡ型証明表を併記する。


¬¬AとAの認識史を組み合わせると認識史00が4行になる。

認識史01で├/を確認できる。
■No.3 非定理 (¬B⊃¬A)⊃(A⊃B) 反対偶律
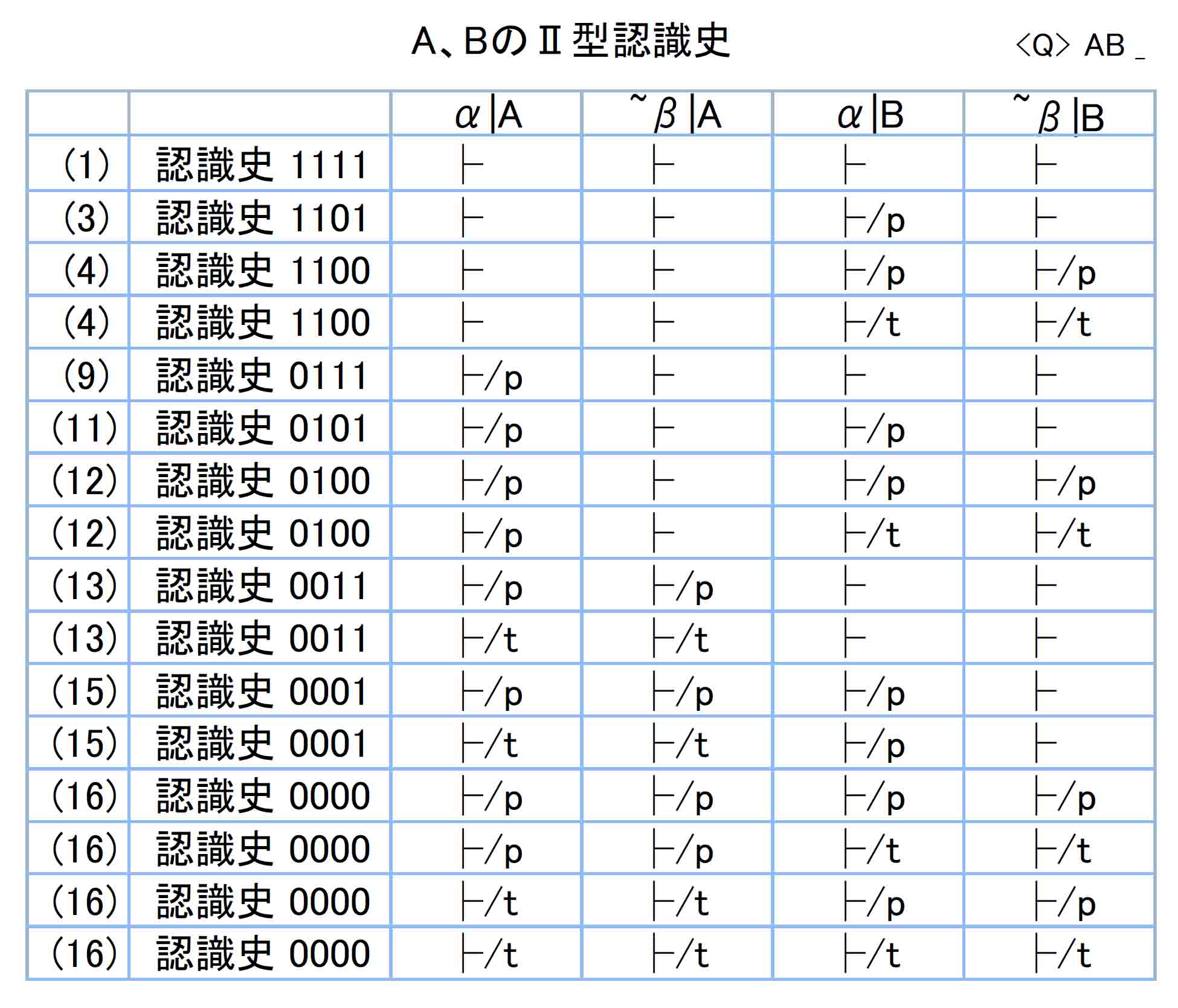
No.10より、¬A、¬BのⅡ型証明表を再録。


列を入れ替えて¬B⊃¬Aの証明表を作成。

同じ認識史で¬B⊃¬Aの値が同じである行をまとめると以下。



偽値演算規則(4)により以下。
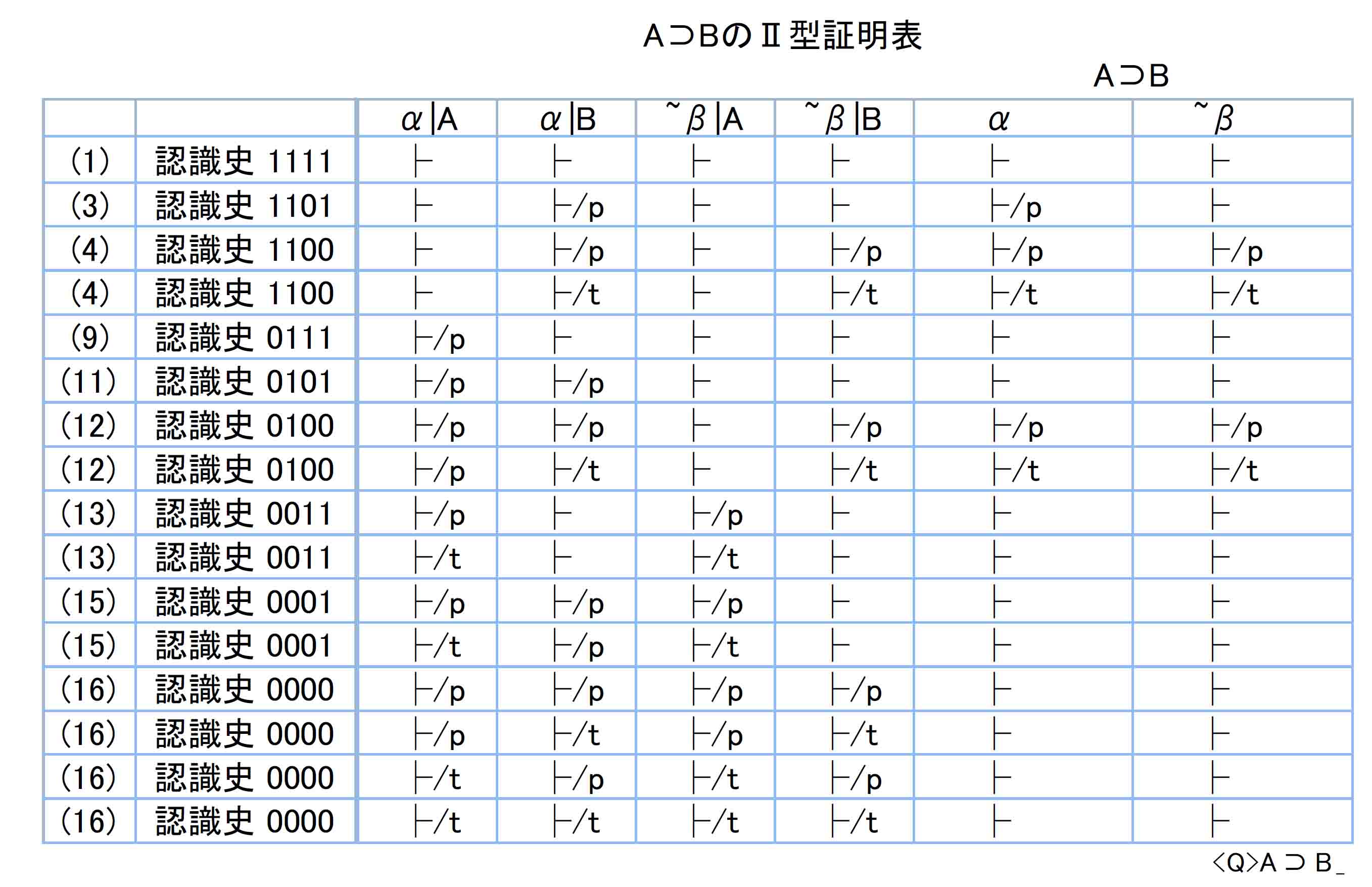
同じ認識史でA⊃Bの値が同じである行をまとめる。
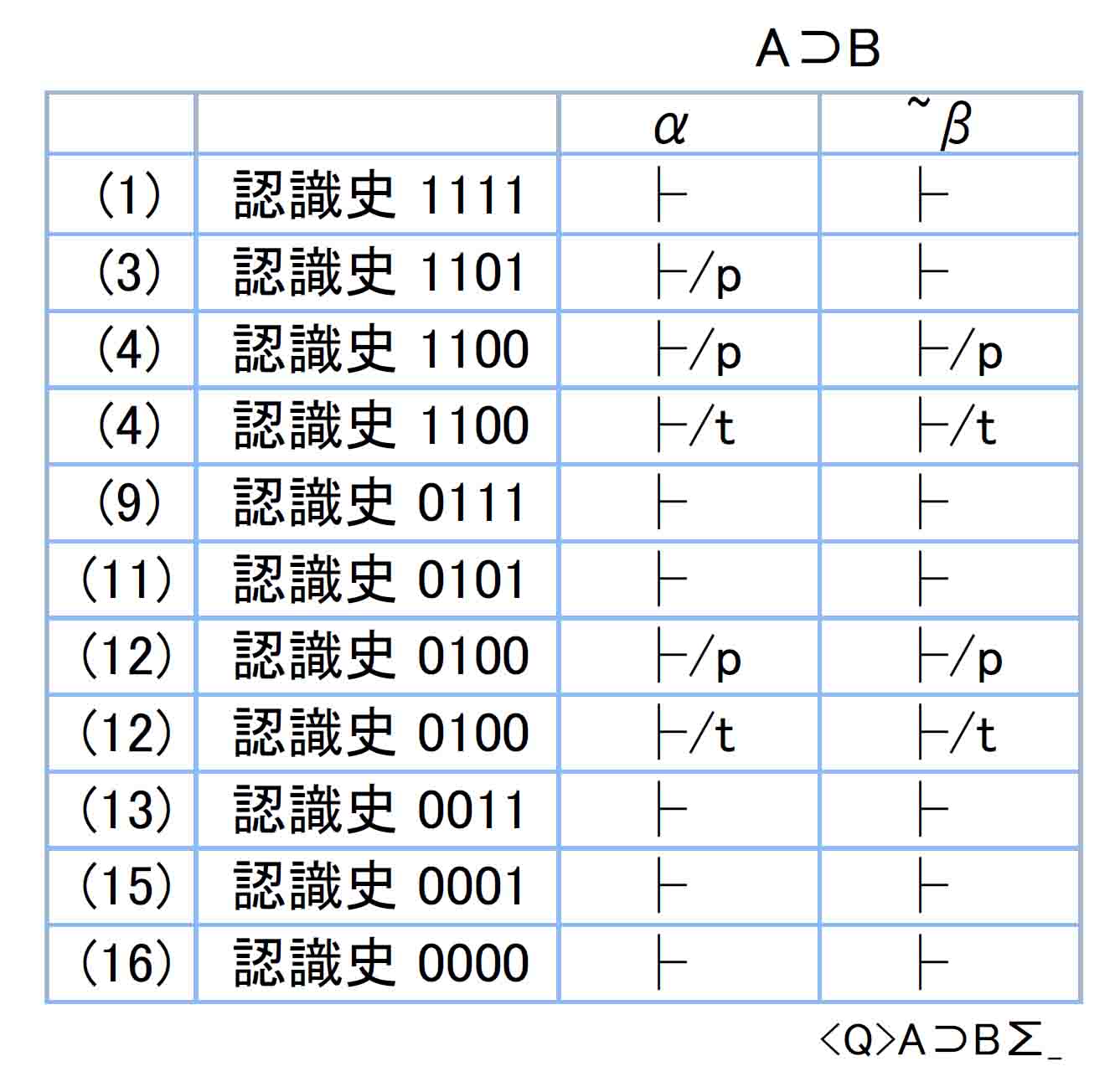
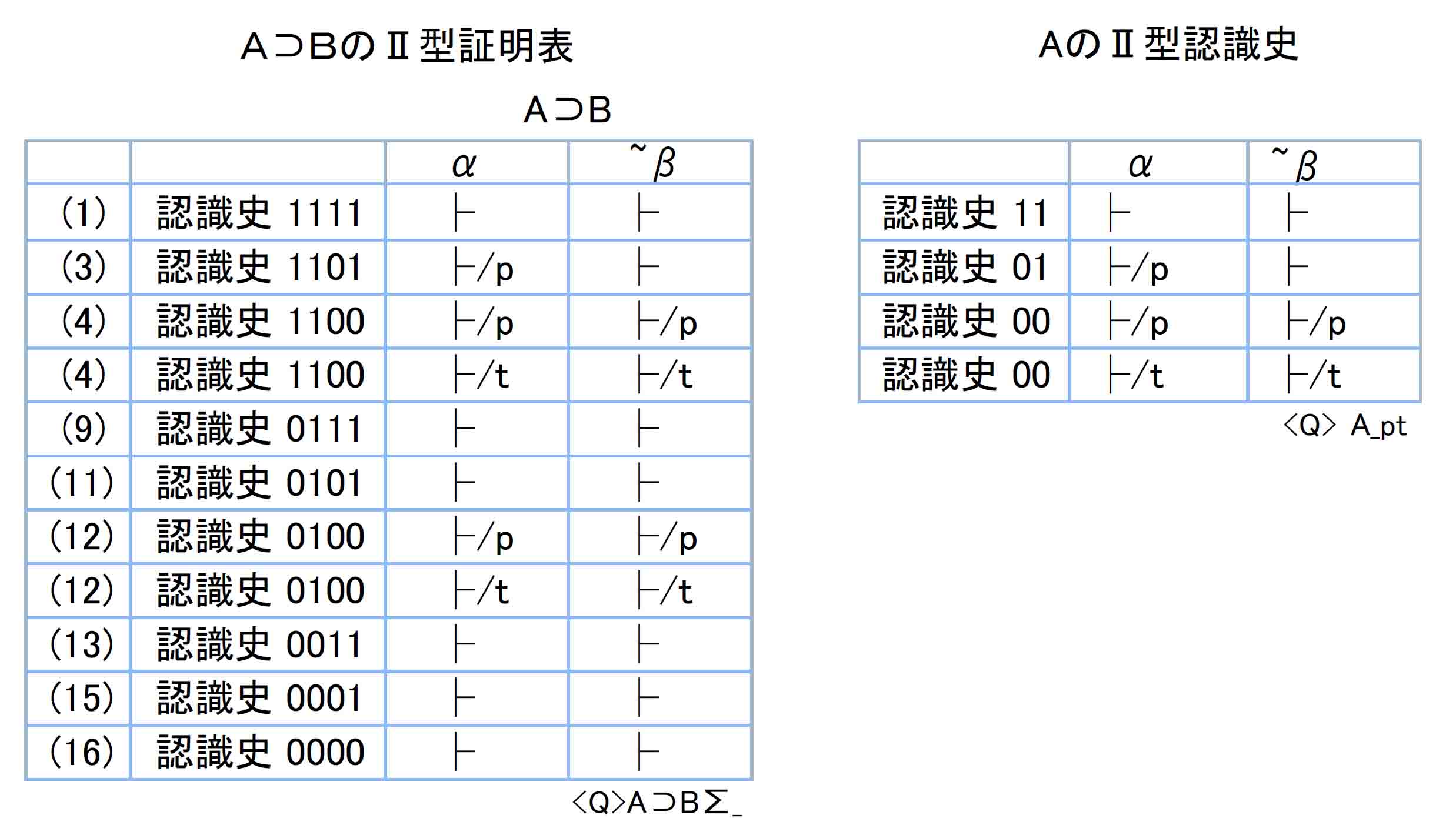
⊃での演算を見やすくするために列を入れ替えてαβ版として作成。¬B⊃¬AとA⊃Bで、認識史1100と0100は各2行あるので組み合せにより、それぞれが4行になる。
⊃(A⊃B)_.jpg)
認識史1101α期の不値によって非妥当式。
■No.4 非定理 (A⊃B)⊃(¬A∨B)
Ⅰ型証明表No.4の「¬A、Bの認識史」において、¬A、Bのどちらかがα├/、~β├/である認識史は2行化され、両方がα├/、~β├/である認識史は4行化される。

同じ認識史で¬A∨Bの値が同じである行をまとめると以下。
A⊃BのⅡ型証明表の偽値を2桁化。

両者を組み合せて以下。
_.jpg)
¬A∨Bの認識史1100、0100の├/pt、├/tpが、前件A⊃Bにはない偽値として存在している。
偽値演算規則(4)3により、前件、後件のいずれかの期に├がある認識史と、前件、後件のすべての期が偽値である認識史を分けて演算処理を行う。
「A⊃Bと¬A∨BのⅡ型証明表」から、├を含む認識史を取り出して偽値演算規則(4)3aの演算を行う。
⊃(¬A∨B)├∑_.jpg)
「A⊃Bと¬A∨BのⅡ型証明表」から、すべての期が├/である認識史を取り出す。
├¬∑_.jpg)
上表のA⊃B、¬A∨Bをまとめると以下。

偽値演算規則(4)3bにより、¬A∨B → A⊃B 方向への外部結合を行う。
⊃(¬A∨B)├¬_.jpg)
├行と├/行に分けた表を結合して以下。
⊃(¬A∨B)_.jpg)
Ⅰ型証明表では以下。(Hard study 5-5-1 から再録)
⊃(¬A∨B)_ProofMatrix.jpg)
Ⅰ型証明表とⅡ型証明表で偽の表れ方が異なっている。
Ⅰ型証明表で├/となっている認識史0101は、Ⅱ型証明表では2種類の偽値によって不証明となっている。
またⅡ型証明表では、Ⅰ型証明表に現れない包含関係による不証明が認識史1100と認識史0100に生じている。これは後件¬A∨Bが、¬によって不証明の二義を含んだ主張となっていることによると理解される。
■No.5 定理 (¬A∨B)⊃(A⊃B) No.4の逆
No.4(A⊃B)⊃(¬A∨B)のⅡ型証明表の列を入れ替えて⊃偽値演算を行うと以下。
⊃(A⊃B)_.jpg)
■No.6 非定理 ((A⊃B)⊃A)⊃A パース律
2命題A⊃Bの認識史4桁の前2桁とAの認識史2桁を対応させると以下。
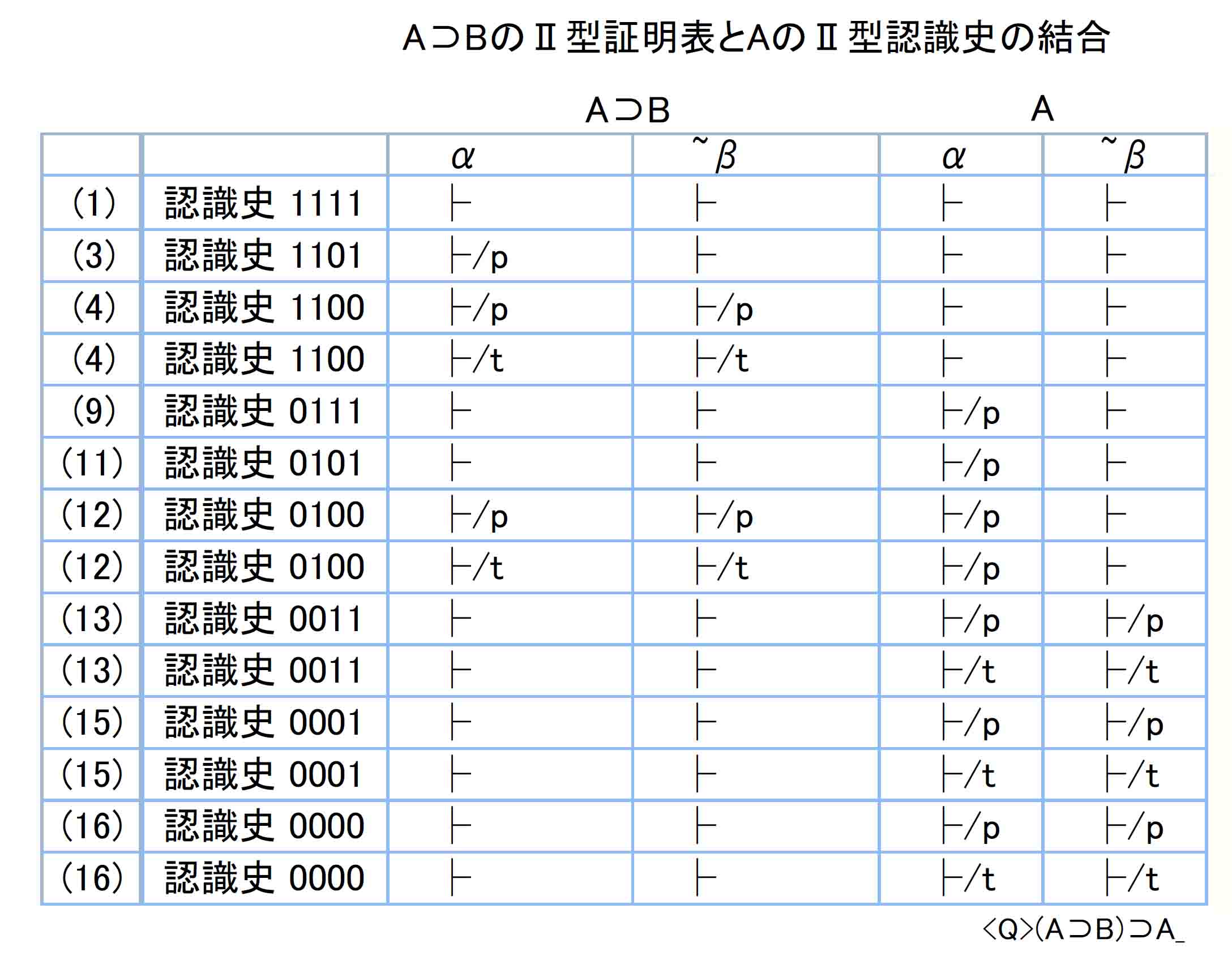
⊃A_.jpg)
⊃A)⊃A_.jpg)
■No.7 非定理 A⊃(B∨¬B)
¬Bの認識史はB由来。B∨¬BのⅡ型証明表は以下。


A⊃(B∨¬B)の認識史は、AおよびB∨¬Bの認識史の組み合せで16行となる。
B∨¬Bに、Aにはない├/ptがあるが、├/ptがある行には├があるので、偽値演算規則(4)1に該当しない。(4)2で計算して以下。
_.jpg)
認識史1101で2種類の├/を確認できる。
以上で、Ⅱ型証明表がⅠ型証明表の拡張であることが示された。