| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (19)
Hard study 5-4-2 ラッセルパラドクスの解決としての直観主義論理(命題関数版)
ラッセルパラドクスの解決のために直観主義論理は何を行ったのだろうか。 パラドクスの命題関数版でみてみる。
命題関数とは主語と述語からなる命題(平叙文)の一部を空欄(未定義)にした命題未前の文の形のことを言い、xを主語、Fを述語とするとF(x)で表される。「xはFである」と読み、xに「ポチ」、Fに「犬である」を代入すると「ポチは犬である」という命題になる。
ここで命題関数ω(x)を考える。これは「xはωである」だが、述語ωを「主語をそのまま述語にして使うことができない性質の述語」とする。
もちろん、すべての述語がこのωの性質を持つわけではない。例えば、述語を「日本語である」とした場合、それがωの性質を持つかは文を作って確かめてみないと分からない。
そこで、述語「日本語である」に、主語『日本語である』を載せてみると、「『日本語である』は日本語である」となるが、これは正しい文になっているので、「日本語である」を述語とする文はω(x)としては成り立たない。ωは、主語をそのまま述語にすることができない述語、すなわちその述語を使ったときに誤った文になる述語でなければならないからである。
述語を「犬である」としたとき、これを主語とする文がどうなるかをみてみる。命題文は「『犬である』は犬である」となるが、主語『犬である』は、「日本語」とか、あるいは「4文字」、「断言」などではありえるものの、少なくとも「犬」ではないので、『犬である』を犬だと主張するこの文は正しくない。
したがって「犬である」は自分自身を主語にできない述語、すなわち「主語をそのまま述語にして使うことができない性質の述語」である。そこで「犬である」という述語はωの資格があり、ここではω(x)は成り立つ。
ω(x)という命題関数が有効であることが分かったところで、このような種類の命題関数ω(x)のxにωを代入してみる。すると命題関数ω(ω)が得られるが、これはどのような命題関数なのだろうか。
まず、命題関数ω(x)は
ω(x)≡¬x(x)
と定義される。この定義は「主語xはωである」という左辺と、「主語xはxではない」、すなわち主語xをxだと述べると誤りになる、
ここで「xであると述べると誤りになる」という述語¬xは、ωに与えられていた「xはそれ自身を述語にして使えない」という述語ωの性質そのものといえる。すなわちω(x)のωは、¬x(x)の¬xのことである。
さて、このようにωを¬xのこととして理解することには何の問題もないようにみえ、『論理学』においてもこの部分は「まず、ω(x)の定義から、次が言えることを確認していただきたい」として、その次行に上の定義式が書かれているだけで、この両辺が同値であることの確認は読者任せとなっている。(p.132)しかし私にはこういうところが難しく感じられる。というのも次のように思うからである。
――左辺のωに内包されていた否定が、右辺でxの外に¬として出ているが、この変換は正しいのだろうか。
x(x)
を考えてみる。これは述語xを主語にした命題関数であり、これを文にすると、例えば先の、
「犬である」は犬である
となる。そして既にみたように、この文は正しい文ではない。そうするとこのときの述語xはωということになるだろう。この文は「主語xをxだと述べると誤りになる」からである。するとωは¬xではなくxなのではないか。
続いて、
¬x(x)
についても考えてみる。これは、
「犬である」は犬ではない
である。
しかしこの文は正しい文である。したがって「犬ではない」すなわち¬xは、ωではないことになる。ωは正しい文として機能してはならない述語だからである。
そしてラッセルパラドクスの議論は古典論理で論じられているものであるから、ここでは排中律が成り立つので、¬xがωでないならばxがωということになる。そもそも「犬である」を述語とした時にそれがωの要件を満たすことは、当段冒頭で確認できていたことであった。したがってωは¬xではなくxである――。
このように考えると、xが、すなわち「犬である」がωのように思われるのだが、しかしこれは野矢茂樹『論理学』にあるωの定義と違っているので、誤った理解であることは必定である。ωはxではなく¬xでなければならない。どこに混乱があるのだろうか。
もう一度初めに戻って確認してみる。『論理学』での説明は次の通りである。
述語「日本語である」をFとする。F(F)は、
「日本語である」は日本語である
となる。これは正しい文なので、述語がFのときはω(F)は成り立たない。
述語「犬である」をGとする。G(G)は、
「犬である」は犬である
となる。この文は正しくないので、述語がGのときはω(G)が成り立つ。以上である。(p.131)
では、ここで成り立つとされたω(G)は何と読むのか。これはG(G)の述語Gをωに取り替えたものなのでωはG、すなわち「『犬である』は犬である」と読むのが正解であるように思える。しかしそうするとこれは先に見た、xを「犬である」とした事態そのままなので、やはりωはxであるということになってしまう。しかし繰り返すがこの理解は誤りなのである。改めてどういうことなのか。
ここでは以下のように理解しなければならない。
『論理学』の記述では、G(G)が正しい文ではないのでω(G)が成り立つと述べられている。つまりω(G)は、G(G)の正しさ、正しくなさという真偽判断が加味された命題関数であり、G(G)そのものではないということである。したがってG(G)とω(G)は同値ではなく、Gがωであるのではない。ω(G)はG(G)に否定判断を加味して「『犬である』は犬である、ではない」と読むのが正解である。
命題や命題関数および論理式には、自身が述べていることと世界の実際との対応における真偽情報は含まれない。論理式は世界に対して「犬であるは犬である」「犬であるは犬ではない」等、主語の肯定が正しい、あるいは否定が正しいという主張を行う文であり、その主張に対する真偽判定を含んではいない。
したがって、G(G)への正しくないという判定を持ちこんでω(G)が作られ、このω(G)をGだけを用いて表そうとするときには、そのGの式は、式に対する外からの判定が持ちこまれた形としなければならないのである。このためω(G)は¬G(G)として表現される。
述語が主語に対する否定でありつつその主語の述語であろうとするとき、そのような述語をωという否定なしの記号で表すことができる。しかし、このωを外からの真偽判定を借りずに、あくまでもその主語xを用いて論理式の中で定義しようとすると、ωが持っていた主語への否定が表に表れるのである。
このとき述語¬xがωの資格を得ているのは、それが主語を否定する述語を表現した記号を持つことによってであるのに対し、先に「犬である」をxとした例で、x(x)の述語xがωの資格を得ているように見えたのは、x(x)という文に真偽判定を行うことで述語xにωの資格があるかを調べただけであるのに、真偽情報をまだ加えられていないこのxをωの表現と見たためであった。このときのxは、ωに内包されている否定を、文に対する真偽判断として自身の式の外に置いたままだったのである。
ここまで、ω(x)≡¬x(x)の右辺で¬が出てくるのはなぜかを考えた。寄り道となったが、命題と世界の関係についての上の理解は、この後、「嘘つきパラドクス」の構造や、直観主義論理の世界観を理解するための助けになるはずである。
さて、定義式の≡の有効性が確認されたところで、パラドクスが起こるのはなぜかを考えてみる。
ω(x)≡¬x(x)というωの定義は「矛盾の根」であって、この段階ではまだ矛盾には至っていない。ここからxにωを代入するところで矛盾が起こる。
ω(ω)≡¬ω(ω)
ここでω(ω)はその否定形である¬ω(ω)と同値となり、ここから矛盾が証明されることとなる。証明手順は『論理学』にある通りだが、集合版と同様、こちらもこの式の形から見て矛盾であることは明らかであるだろう。
そしてやはり直観主義論理は古典論理で発生するこの矛盾を回避するために考えられた論理学ということである。どのように回避したのだろうか。
否定的に規定された主語への言及が行われるところに起こるパラドクスとしては「嘘つきパラドクス」がある。これは『論理学』に紹介されている「自分でひげを剃らない人のひげだけを剃る床屋のパラドクス」、「自分が市長をしている市に住まない『不在市長』のパラドクス」と同様、ラッセルパラドクスの普及版の一つで、そこでも同じことが起こる。
ある人が「私が言うことは嘘である」とだけ述べた場合、この言明の真偽を問題にするとパラドクスとなる。この言明を真とみなせば、言明通りとなり彼は嘘を言っていることになり、偽りとみなせば彼は本当のことを言っていることとなる。いずれも初めの仮定が否定されて言明の真偽が定まらない。
この「嘘つきパラドクス」についての解釈や解決法は多数行われているが、私は次のように理解する。
通常の命題では、命題の主張に対する判定者は世界である。G(G)とω(G)についての考察でみたように、命題の主張は「真理の対応説」によって真理判断が行われ、命題が述べていることは世界との対応おいてその真偽が量られる。これが古典論理が想定している命題の真偽構造である。
当節冒頭でのω(x)についての判断は、この点を如実に示している。そこではωを「犬である」としたときに「『犬である』は犬である」が誤った文となることから、これをω(x)として認めたのであった。
これは、述語側の「犬である」を世界に存在する実際の生き物への指示語とみて、主語の「犬である」という文字列には適用できない用例と判断したということであり、命題の真偽の基準として、「命題の主張」と「世界の事実」間に「真理の対応説」を働かせて命題の真偽を決定しているということである。(なお、ここでの主語『犬である』が単なる文字列に過ぎないと解されなければならない理由については注
一方、「『日本語である』は日本語である」については、これも同様に、述語側の「日本語である」を実際の日本語を指す語とみて、主語の「日本語である」という文字列に適用できる用例と判断したということである。同じく「真理の対応説」を働かせてこの文の真偽を判断した結果、こちらは正しい文とされたのである。
仮に、これらの命題に適用する真理基準を「真理の対応説」に限定しないならば、つまりこれらの命題文がそもそも世界との対応に拘(こだわ)っていないと考えた場合、これらは誤った文ではなくなる。というのは、「『犬である』は犬である」および「『日本語である』は日本語である」は、「AはA」と同様の同語反復として読むことができ、その場合、これらの文は「真理の整合説」の「同一律」により真と判断されるからである。
ちなみに「『犬である』は犬である」や「『日本語である』は日本語である」などの繰り返し文は、その述語部分を世界に対応を持つ語としてではなく、すなわち意味を持つ語としてではなく単なる文字列として解した場合は、すべて真となる。
したがって、「犬である」が主語のときにはω(x)が成立し、「日本語である」が主語のときにはω(x)が成立しないとする判断は、命題と世界を「真理の対応説」において判定して、その真偽を決定していることを示しているのである。
そしてこの判断は、これらの命題に対して特別な扱いをしたというのではなく、命題一般に対する操作として行われたのであるから、我々は命題というものを「真理の対応説」すなわち「命題とは世界の事実について述べたものである」という見方で扱っているということがいえる。
このことのゆえに、通常の命題においては「世界による真偽判定」が機能するのであるし、また、我々は命題をそのような扱いを受けるべきものとして理解しているのである。
しかしω(ω)や「嘘つきパラドクス」では、述べられている対象すなわち主語が自分自身になっている。自己言及命題ではこの点が特異なのである。
では、「『犬である』は犬である」や「この文は偽である」のような、述語や命題自身を対象として述べられた命題の真偽を判定するのは何なのだろうか。命題から独立して存在する世界や特定の事実がない場合、その言明に真偽を与えることができるのはその言明自身を置いて他にはない。
つまりこの状況では、古典論理が想定している「世界に対する主張文」としての命題、およびその命題から「独立して存在する判定者」としての世界という構造が失われ、命題とその判定者が循環構造になっているのである。
言いかえればこのような命題は、世界に対する通常の真偽主張を行えていない命題になっているということである。
「私は嘘を言っている」と言った場合、その言明は世界について述べているのではなく自分について語っている。より正確に言えば、語っていることそのものについて語っているのであり、その「語り」が本当か嘘かを判定する、「語り」から独立した事象というものは存在しないのである。
このような構造を持たされた命題に対して、それを通常の命題文のごとく改めて外から真偽判定をしようとしているところにパラドクスが起こる。ここもより正確に言い直せば、そこで行われようとしている判断を、命題の外からの通常の真偽判定として行えるものと思っているところで錯覚が起きているということである。
それは童話「白雪姫」の后が鏡に問いかける場面と似ている。
后は「世界で一番美しいのは誰か」と鏡に問う。世界を映す魔法の鏡は后の問いかけに対して判定を行い、后が一番美しいとか、白雪姫が一番美しいと答えるのである。
ところがある時、この鏡は普通の鏡になってしまっていた。それを知らない后はいつものように鏡に訊ねる。誰が一番美しいか。鏡は沈黙している。そこでもう一度訊ねる。誰が一番美しいか。それはあなたです、と鏡は答えた。
しかし答えたのは鏡ではなく、鏡に写っている自分だったのである。后はさらに問い続けるが、彼女がわたしが美しいと言えば后が美しく、白雪姫が美しいと言えば白雪姫が美しいことになる。鏡の答えは彼女次第なのである。
鏡がもはや魔法の鏡ではないことに気がつけば、后は鏡の答えを不思議には思わなくなるだろう。しかしこの鏡を世界を映す魔法の鏡と思い込んでいる限り、彼女は鏡のパラドクスに捕らわれたままとなるのである。
自己言及文のパラドクスというのは、この喩えのように魔法の鏡がただの鏡になっているときに、すなわち命題から古典論理の構造が失われ、命題の真偽が我々の見なし方次第となっているときに、その見なしによって起こる二通りの帰結を、通常の「世界による命題への真偽判定」と見誤っている状況のことなのである。
なお、自分自身についての言及であってもそれが肯定的な内容の「ほんとつき文」の場合にはパラドクスは起こらないとされている。これはどういうことなのか。
しかしおそらくこれは思い違いであって、上のパラドクスと同じ状況は起きているのである。ただ、肯定言及の場合はそのように感じることが難しいということである。
誰かが「私は本当のことを言っている」と言った場合、これを肯定すれば彼は真実であり、嘘と見なせば彼は偽り者である。ここでも彼の真実さはそれを判定する者次第となっている。
しかしここでは否定言及のときのように、肯定すれば否定、否定すれば肯定という逆転現象がないために、真偽が定まらない点は同じでありながらも、「ほんとつき文」でこれを奇妙な感じとして受けとることは難しいということであるように思われる。
しかしこのような肯定自己言及の場合も、命題から独立した世界による判定という古典論理の命題構造が失われている以上、その言明は通常の確かさを持つことはない。
このことは、人が確かめる術のないことをまことしやかに語った後に「私が言ったことは本当だ」と宣言し、さらに続けて次の決まり文句を述べるところに如実に表れている。曰く――信じるか信じないかはあなた次第――。
ということで、やはりこのところにこの言明の破れは見えているというべきだろう。自分についての証言は、それが肯定のものであれ否定のものであれ証明する他者を持たないのである。
これに関連して、ヨハネ福音書がイエスの相矛盾した自己言及を伝えていることは興味深いことであるかもしれない。
「もしわたしだけが自分のことを証言するのなら、わたしの証言は真実ではありません。」(ヨハネ5.31)
「もしこのわたしが自分のことを証言するなら、その証言は真実です。」(ヨハネ8.14)
イエスにおいても自己言及はパラドクスなのだろうか。
さて、それはともかくとして、こういったパラドクスが起こらないようにするために、言いかえれば世界による命題判定という構造が損なわれないようにするために、直観主義論理は何を行ったのかということであるが、私の理解では、直観主義論理は否定記号¬に古典論理の¬とは異なる意味を新たに加えることによってこの事態を回避したということだと思われる。
ω(x)≡¬x(x)における¬xのxに、ωを代入することを認めないことにしたというのが「論理主義」の立場をとるラッセルによる解決法で、彼は矛盾を引き起こすωについて「述語ではないと結論せざるをえません」と述べているということである(同書p.133)。これは前段でみた集合版で、MがM自身の元であるかを問うこと自体を不適切としたのと同じく、ωがωの述語であるかを問うこと自体を拒否したものと解せる。
そして、先に命題と世界の関係についての考察を経てきた我々は、ラッセルがωについて「述語ではないと結論した」ことの意味はよくわかる。それは、ωのような自己言及文の述語は世界について述べたものではない、すなわちそれは古典論理で想定されてきた述語ではないということなのである。
ただしいずれにせよこの「ラッセルの解決法」に留まると、前節のときと同様、それ以上の理解を求めることが難しいと思われるので、ここでは¬記号の解釈にその手がかりを求めて、直観主義論理がこのパラドクスのために何を行ったのかについていくらかの理解を試みたい。
Hard study 5-2-4の「直観主義論理の¬¬P⊃Pの証明表」で、直観主義論理が二重否定除去則を公理としないことを見たが、もし、¬¬P⊃Pにおける¬の意味が古典論理の¬と同じであるなら、これを公理として認めない理由はない。直観主義論理においてこれが公理ではないということは、直観主義論理の¬は古典論理の¬とは違う意味と働きを持つものとして再設定されていることを示している。
もちろん「真理の整合説」に則る論理学において、その出発点たる公理は任意でよく、¬¬P⊃Pを公理に入れないことの意味を示すことは必ずしも必要ではない。Hard study 5-2-2で見た「公理系0-1」のような意味を持たない体系もある。しかし古典論理も直観主義論理も、その公理には意味論が備わっており、この意味論は論理学の出発点たる諸公理を現実世界へ結ぶためのものである。
したがって¬¬P⊃Pを公理としないということは、これを公理とする論理体系に対する異議となるものであり、その公理系が現実世界から乖離しているという認識を示すものともいえる。端的に言えば、否定を二度繰り返すと肯定になる、という「否定」に対する古典論理の考えが、現実世界における否定という状況を正確に捉えていないことを主張するものなのである。
そこで以下の考察では、直観主義論理が、否定記号¬に古典論理の¬とは異なる働きを加えることによって、ω(x)の定義から導かれるとされた、ω(x)≡¬x(x)が常に成り立つことにならないようにした、という見通しに立って、これを確かめていくことにしたい。
ある論理式を公理としない、あるいはそれが定理ではないということは、その式が常に成り立たないことをいうものではない。例えば、古典論理において「(A⊃B)かつB からAを導出してよい」という後件肯定式は定理ではないが、これはこの論理系において後件肯定式が常に成り立たないことをいうものではない。Easy Study 3の「昨夜の雨」の例のように、後件肯定式推論が成立する事例はたくさんある。ただし常に成り立つわけではないので定理ではないのである。
直観主義論理の二重否定除去則についても、これが公理ではないということは、直観主義論理において二重否定除去が絶対に成り立たないことをいうものではなく、常に成り立つわけではないことをいうものである。実際、二重否定除去則は、先の「¬¬P⊃Pの証明表」によって、認識史11と認識史00では成立することが確認できる。
これと同様に、ここではω(x)≡¬x(x)が、ω(x)の定義から常に成立するものなのではないことを確認したい。すなわち、上式にωを代入する以前の段階のω(x)≡¬x(x)という式そのものが、直観主義論理においては妥当ではないということである。
ラッセルパラドクスの命題関数ω(x)の定義式の右辺
¬x(x)
の¬は、直観主義論理が構築される以前の古典論理において考えられている¬であるから、当然それは古典論理による否定の働きをして、主語を述語にして文を作ると文が成り立たないことを意味する¬である。
しかしこれにより¬xはωの性質をそのまま表したものとなるので、古典論理においては、¬x(x)はω(x)と≡で結ぶことができる。ただしそれによってラッセルパラドクスが生じる。
そこで直観主義論理は、この¬に、古典論理における真偽の意味での否定、つまり真偽を逆転させる働きとしての否定ではない別の働きを合わせ持たせることにした。
それは「証明可否」のような概念である。直観主義論理での新たな否定記号¬には、古典論理が持っていた真理値の逆転としての否定の他に、証明値の逆転としての否定という二つめの働きが与えられたのである。
このことは、意味論の初めに立ち戻って、命題Pの認識史を眺めてみることからも得られる理解である。下にHard study 5-2-4からPの認識史を再録する。
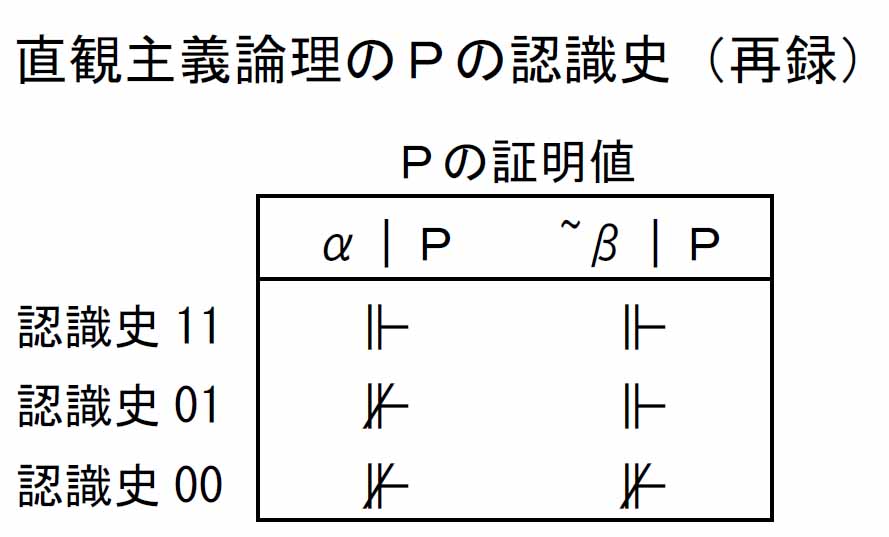
認識史01と認識史00の頭初期αで、命題Pはいずれも⊮である。しかし、認識史01では最終的に⊩となり、認識史00では⊮のままである。これは認識史01では命題Pは真であることが証明されたということであるのに対し、認識史00では最後まで証明されなかったということである。
つまり認識史01における⊮は、本当は真であった命題Pの真であることが当初はわからなかったということであり、そこでの⊮は不証明の⊮であるということである。
これに対して認識史00での⊮は、命題Pが最後まで証明されなかったということであり、それはHard study 5-2-2での意味論読み替えⅡ(5)(ハ)「後続期すべてで命題Pの肯定が証明されない場合、頭初期で否定が証明されている」に該当する。つまり構成主義の世界観における認識として、頭初期での命題Pの偽を宣言するものである。すなわち認識史00でのα⊮は否定の⊮である。
直観主義論理意味論では、⊮記号と古典論理由来の¬記号が使い分けられるが、しかしこの時点ですでに⊮記号に意味の二重性があるということである。そしてこの二種類の⊮は、直観主義論理構文論において¬記号一つで表現されることになる。つまり、直観主義論理で我々が目にする¬記号には二重の働きが含まれているのである。
そこで、¬xは
「主語をそのまま述語にすると文としての正しさが誤りとなる性質の述語」――(ア)
の他に、
「主語をそのまま述語とすると文としての正しさが証明できない性質の述語」――(イ)
という二つめの意味を持つこととなる。(ア)は文の誤りを主張するものであるのに対し、(イ)は文の真偽不明を主張するもので、両者の主張は異なる。このため¬x(x)とω(x)は、常に成立するという意味での≡では結ぶことができなくなる。ωには(ア)の定義しか与えられていないからである。そして同値記号で結べなければ矛盾も生じない。
この状況を先の命題で確かめてみる。
古典論理での¬x(x)は
「『犬である』は犬である」ではない ――d
という断定である。
直観主義論理の¬x(x)は
「『犬である』は犬である」ではない ――d
「『犬である』は犬である」は証明できない――e
の二つのうちのいずれかを意味するものとなる。
一方で、元々古典論理で考えられたω(x)は、それを直観主義論理に持ってきても「主語『犬である』を述語にできない述語」のままであるから、直観主義論理のω(x)は上のdに相当する。
そこで、直観主義論理の言明¬x(x)がdの場合、¬x(x)≡ω(x)は成り立つ。しかしeである場合は成り立たない。したがってdとeの区別を持たない¬記号を含んだ直観主義論理の¬x(x)は、ω(x)と≡で結ぶことができない。それによってラッセルパラドクスが避けられるのである。
自己言及ではない一般的な命題でも確かめておこう。
命題Aを「太郎が山に登った」とすると、古典論理における¬Aは「太郎が山に登らなかった」である。
直観主義論理では、命題Aは「太郎が山に登ったのを見た」である。ここで「見た」が付け加わることで、古典論理の命題Aとの対応性がないように感じられるかもしれないが、実は、「見た」に相当する言葉は古典論理の命題にも含まれている。
直観主義論理の証明値に相当するのは古典論理の真理値であり、したがって直観主義論理の「見た」に相当するのは古典論理の「真である」である。しかし古典論理では「真理の余剰説」によって、「真である」という言葉はあってもなくても意味に変わりはないとされるため通常の命題文では省略されるのである。
そのため先の命題Aの正式な形は「『太郎が山に登った』は真である」、¬Aの正式な形は「『太郎が山に登らなかった』は真である」ということであり、直観主義論理の「見た」に相当する文言はここに含まれているのである。したがって直観主義論理とは「真理の余剰説」によって省略されていた古典論理の「真である」の部分を、「見た」「証明済」などに変えて「いじった」ものと解することができる。
そこで命題A「太郎が山に登ったのを見た」が、直観主義論理で否定された場合には二通りの文言が考えられることになる。
「登った」が否定されたとして「太郎が山に登らなかったのを見た」と解することもできるし、「見た」が否定されて「太郎が山に登ったのを見なかった」と解することもできる。
古典論理では否定のこのような二重性は起こらない。容易に確かめられるが、「登った」を否定しようが「真である」を否定しようが、いずれも「登らなかった」に帰着するためである。
すなわち、古典論理においても否定の二重構造そのものは存在している。命題Aは「登った」を否定して反対命題とすることもできるし、「真である」を否定して外からの真偽判断としての否定を加えることもできる。しかし命題に与える効果はいずれも同じであり、これによる命題の二重化は起こらず、「太郎は山に登らなかった」に帰着するのである。
つまり、古典論理とは「命題自身の肯定否定」と「命題に対する真偽判断」を区別しない論理学なのである。
これに対して、直観主義論理での命題Aの否定は、それが否定の意味での否Aであれ、「見なかった」など、不証明の意味での不Aであれ、ともかく「Aではないこと全般」としての「非A」である。この非Aとしての直観主義論理の¬Aは、否Aに限定された古典論理の¬Aとは異なる。
直観主義論理は、¬記号「非」に「否」と「不」を内包させることにより、「命題自身の肯定否定」と「命題に対する真偽判断」を区別する論理学となっている。もっともその真偽判断とは、もはや事の真偽ではなく、その証明可否ということであるが。
繰り返しとなるが、ω(x)のωに含まれている否定は古典論理の¬としての否定である。ところが直観主義論理で¬x(x)と記述したときの¬は、古典論理の¬としての否定の他に、不証明の意としての否定である可能性を持つ¬である。
そしてこのことから、直観主義論理では二重否定除去則(「否定の否定は肯定」という規則)を公理にできないということも起こる。
命題Aを「太郎は山に登った」とすると、古典論理における「¬Aの否定」すなわち¬¬Aは「『太郎は山に登らなかった』のではない」つまり「太郎は山に登った」であり、最初の命題Aと同じになるため¬¬A≡Aとなる。
一方、直観主義論理での命題Aの否定は
「太郎が山に登らなかったのを見た」 ――f
「太郎が山に登ったのを見なかった」 ――g
のいずれかであり、これをさらに否定した¬¬Aは
「太郎が山に登らなかったのを見なかった」――h
「太郎が山に登ったのを見た」 ――i
の二通りに収まる。
そこでiの¬¬AはもとのAと同じ文言だが、hの¬¬Aは元のAとは異なる主張である。太郎が山に登らなかったことが目撃されていない(h)からといって、太郎が山に登ったことが目撃されている(命題A)ことにはならない、というのは常識的理解でもあるだろう。
Hard study 5-2-4の「直観主義論理の¬Pの証明表」に照らして確認すると、「太郎が山に登らなかったことが目撃されなかった」場合というのは認識史11と認識史01に相当する。(「太郎が山に登らなかった」は¬Pに該当するので、「¬Pの証明値」のうち、α期と~β期が「目撃されなかった」相当の⊮となっている認識史11および01)
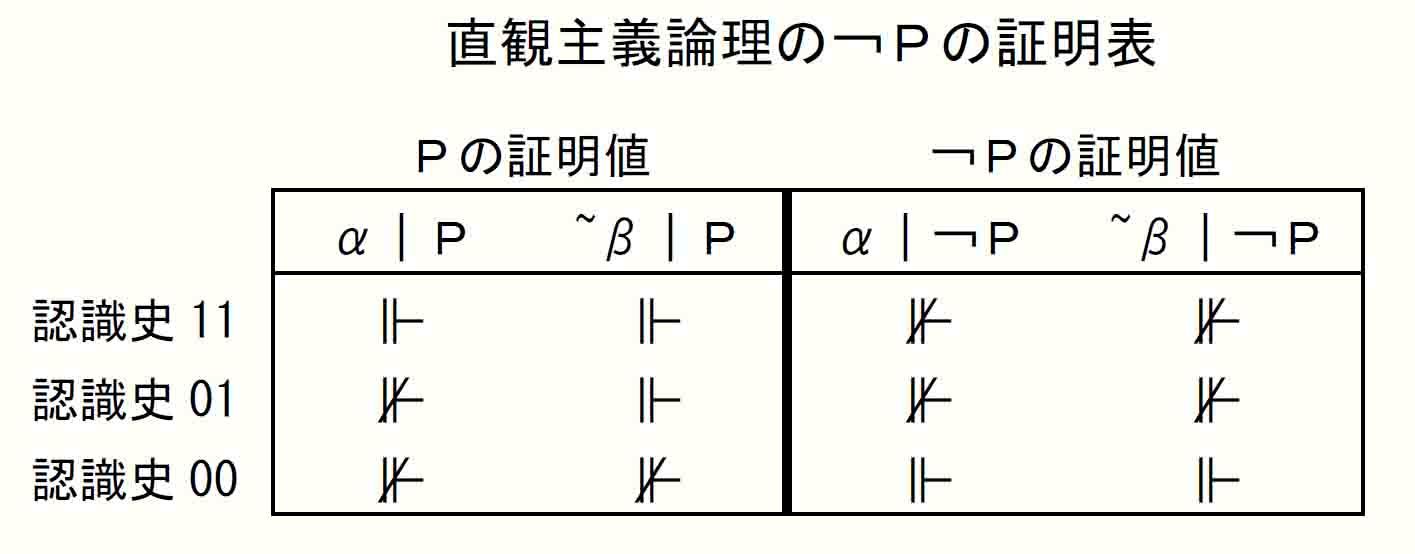
このとき、認識史11ではα期、~β期ともにPについて⊩なので、「太郎が山に登ったのを見た」(i)ということだけが「太郎が山に登らなかったことが目撃されなかった」事態と両立が可能なものとしてあるが、認識史01ではα期で「太郎が山に登ったのを見なかった」(g)という別の事態が両立可能な事態としてあるので、(i)、(g)のいずれであるかは不確定となる。
したがって、太郎が山に登らなかったことが目撃されていない(h)からといって、太郎が山に登ったことが目撃されている(命題Aすなわち(i))ことにはならないのである。
このように、直観主義論理での非Aの否定は、当然ながら、¬¬Aすなわち非非Aではあるが、しかしこの非非は相殺可能である否と否の組み合せ(fからi)や、不と不の組み合せ(gからi)として起こるとは限らず、否と不の組み合せ(fからh)であったり、不と否の組み合せ(gからh)でありえるため、二重否定が必ずしも肯定文iに帰着するとは限らず、二重否定文hに帰着することがあり、このため二重否定記号を除去することができないということである。
こうして¬に新たな意味を付加した直観主義論理においては、二重否定除去則が常に成り立つわけではないことから二重否定除去則は公理から外れている。
直観主義論理は「世界について何を知りえるか」を真理の中心概念とし、否定の意味に「証明不可」を加えることで、否定概念を古典論理の否定概念からずらし、これにより否定の否定が肯定になるとする二重否定除去則を成り立たないものとした。
この「二重否定除去則の拒否」を帰結させる直観主義論理の¬の新たな定義は、古典論理の否定概念を保つω(x)と、直観主義論理の¬x(x)の同値性を壊し、それによってω(ω)の矛盾を回避したのである。このところで、ラッセルのパラドクスの回避と直観主義論理の二重否定除去則の拒否が結びつく。
なお、直観主義論理での¬の意味の二重性については、Hard study 5-2-4に挙げた「直観主義論理の¬¬Pの証明表」からも確認できる。Pの二重否定のあり方は、「直観主義論理の¬Pの証明表」では⊮¬Pだが、「直観主義論理の¬¬Pの証明表」では⊩¬¬Pである。この表現の違いは、上に述べてきた否定概念の二重性の表れといえる。
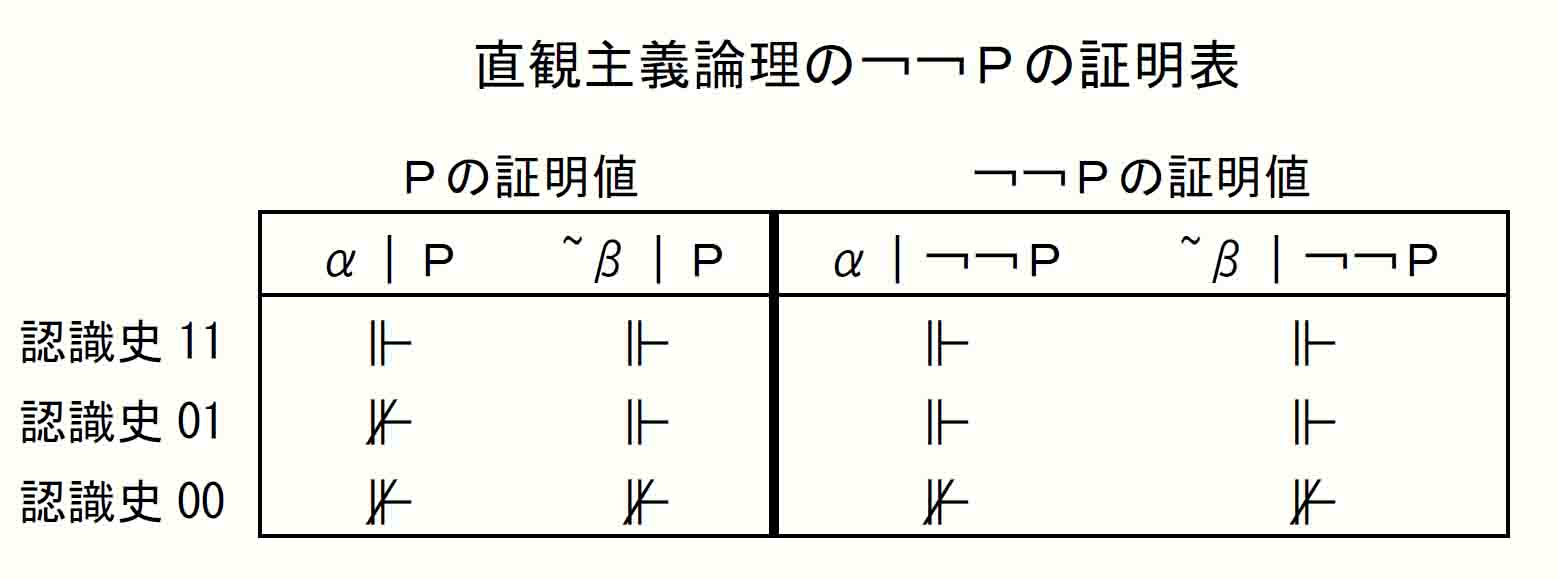
また、「直観主義論理の¬Pの証明表」と「直観主義論理の¬¬Pの証明表」の証明値を比較すると、¬¬Pは¬Pの証明値を逆転したものとなっている。ここでは古典論理と同様に、証明値が証明済⊩から未証明⊮になり、また、未証明⊮から証明済⊩になることが¬の働きである。
一方で、「直観主義論理の¬Pの証明表」での¬Pの証明値は、Pの証明値を逆転させたものではない。同じ¬の付加において、¬Pから¬¬Pへの付加と、Pから¬Pへの付加で、証明値の変化具合が異なるということからは、これらの証明表だけからは窺い知ることのできないものが¬の働きの中にあると感じられる。
その点は後の考察課題とするとして、すでに見てきたように(Hard Study 5-3-1)直観主義論理では¬PはPの真理値から自由な言明である。Pと¬Pの間には古典論理でのような従属関係はない。それらは肯定/否定の関係を保ちつつも定理となるような排中律の関係にはない。
古典論理の排中律は肯定/否定の両者を合わせると、それが述べようとする世界の在りよう全体を網羅することになる言明である。しかし直観主義論理の否定側には「否定」と「不明」の二つがあり、直観主義論理の¬記号は、その都度そのいずれか一つを示すものであるため、それと肯定を合わせても事象の全体を網羅することにはならない。そのため直観主義論理では排中律は定理にならないのである。
以上のように、直観主義論理¬には「否」と「不」の二義が含まれるということである。繰り返すと、直観主義論理での¬Pは古典論理の否Pではなく、また直観主義論理で新たに導入された不Pに限るというのでもなく、そのいずれかであるものとしての「非P」である。
この点は『論理学』においても、p.166 6行目にある「¬¬Aが証明された」の結論として7行目に「¬Aは証明されえない」と述べられていることや、p.245で「そこで『おかしくないことはない』を考えてみると、これはつまり『おかしくない』ことが証明できないという意味だ」とあることからも確認できる。直観主義論理構文論では「ない」は古典論理的な「ない」である場合もあるし、また「証明できない」という新たな意味で使われる場合もあるということである。
さて、これまでに述べてきた直観主義論理におけるω(x)と¬x(x)の同値性の回避は、ω(x)をあくまでも古典論理で定義された¬xとして、すなわちそれを「否定」の意味に限定して扱うことによって可能となるものであった。しかし、ω(x)を直観主義論理の¬が持つ二重性を保ったままでω(x)≡¬x(x)と定義するとどうなるのだろうか。この場合、やはりパラドクスは起こるのではないだろうか。
しかし、直観主義論理の¬記号は「否」と「不」の二重性を持つとはいえ、それはその両者を同時に合わせ持つということではなく、「否」か「不」のどちらかであるということである。正確にいえば、¬記号はその起源が意味論の⊮であるとき(というのは意味論においても¬があるので)、α期においては「否」と「不」の二重性を持っている。
「¬Pの証明表」認識史01と11に見た通り、そこではいずれも⊮だからである。この⊮が「否」と「不」のいずれであるかは~β期の状態を待って初めて決定される。ただしα期のそれは、二重性を持ってはいるが「否」と「不」のどちらかであることには違いない。
ωについても同様で、ωを二重性のある¬を用いて定義する場合、¬の意味に応じたいずれかの意として定義しなければならないので、ωもやはり「否」か「不」のどちらかの意味になる。そうすると、ω(x)と¬x(x)の関係は、意味の組合わせにおいて4通りとなり、その中の2通りが同値にならないため、ω(x)と¬x(x)は≡で結ぶことがやはりできないことになる。
なお、直観主義論理の¬記号が「否」か「不」のどちらかでしかありえないことについては、先の排中律の説明から理解されるところである。繰り返すと、もし、直観主義論理の¬記号が「否」と「不」の両者を合わせ持つということであれば、「A∨¬A」は、それによって全世界を満たすものとなり、したがってそれは定理であるはずである。直観主義論理で排中律が定理ではないということは、¬Aがその都度「否」か「不」のどちらかであって、その両方ではないことを示しているのである。
ここで前段の問い「無限集合を完結したものと見ずに構成されていくものとして見ることによってパラドクスを回避したというその部分は、直観主義論理のどこに認められるのだろうか」を思い起こすと、次のように答えることができるだろう。
直観主義論理が無限集合を完結したものと見ずに構成されていくものとして捉えたことは、直観主義論理が真理概念を事実の真偽という二値から、証明の可否という二値に変えたところに認められる。それは「証明される/証明されない」という二値ではなく、「真であることが証明される/偽であることが証明される」としての二値である。
真であることが見い出される、あるいは、真と仮定したときに矛盾が見い出されるという、いずれも真偽について証明されることをもって真理とする真理観は、証明されない事態というものをいったん論理の外に置くことで排中律を定理としない体系となる。
ここで「いったん」というのは、直観主義論理においても、これまでに見てきたすべての「証明表」が示す通り、どのような論理式も最終的には、すなわち~β期では「真であることが証明される/偽であることが証明される」のいずれかに至るからである。~β期で⊮である論理式は必ずα期でも⊮だが(直観主義論理においてα⊩、~β⊮という事態はない)、このように「証明されない」が認識史の全期に亘るとき、直観主義論理はそれをもって「偽であることが証明された」とする。(意味論読み替えⅡ(5)(ハ))
前段および前々段の終わりに確認したが、直観主義論理においては証明や証言あるいは「見た」などの感覚的な言明から独立して存在する事実というものはない。事実はそれらの認識が「構成」するのである。したがって、ある命題が証明されないとき、すなわちその命題の真であることの認識が最後まで得られないときは、その命題に対応する事実は構成されず、その命題は偽なのである。
これが直観主義論理における「構成主義的なものの見方」であり、これにより最終的に排中律は成立するものの、認識途上においては排中律の定理性は拒否される。Hard study 5-2-4の「P∨¬Pの証明表」の通り、排中律が真とならない事態はα期に表れるのである。そして、排中律の拒否からは二重否定除去則の拒否が導かれる。
つまり直観主義論理におけるこの「構成主義的なものの見方」こそが、ω(x)と¬x(x)の同値性を壊し、ラッセルパラドクスの回避につながるものなのである。
さて、ラッセルパラドクスの回避のために、直観主義論理は、¬に古典論理の「否」の他に「不」を加えて二重の意味を持たせ、ω(x)と¬x(x)を≡で結ぶことができないようにしたという上の理解には、次の別の理解をさらに加えることができるかもしれない。
すなわち、直観主義論理では命題の真偽判定として、古典論理が想定する「命題と世界の対応性」という捉え方のみを認めるのではなく、「命題内での整合性」という捉え方も認めることにしたということである。
「嘘つきパラドクス」について述べたところで、「『犬である』は犬である」は、「AはA」と同様の同語反復として読むことができる、としたが、この読み方を認めると、ω(x)の資格があるとされたこの「『犬である』は犬である」はω(x)ではなくなる。同語反復は正しい文だからである。
言いかえれば、この言明は真理の対応説的には「犬である」を犬だと主張する誤った文であるので、その判断を加えると¬x(x)となり、それはω(x)だが、真理の整合説に立てば「犬である」は「犬である」に他ならず、これは何ら誤りではないから、その誤りではないという判断を加えたものはx(x)のままであってω(x)にはならない。
このように、主語述語の繰り返し文は、それに対する真理基準の取り方の違いからくる真偽の二重性を帯びた文である。直観主義論理は、この「繰り返し文」を世界対応として読むことの他に、同じ語の整合的反復として読むことを許可し、それによってこの「繰り返し文」を¬x(x)と定義することの他に、x(x)とも定義したというようにも解釈できる。
すなわち、命題の真偽判定に整合説を導入することの結果として、「『犬である』は犬である」のような繰り返し文が、対応説による¬x(x)とは別に、x(x)を同時に帰結させることとなる、ということによって、これを矛盾命題となるようにしたということである。
この見方に立つと、直観主義論理において「『犬である』は犬である」は、¬x(x)であると同時にx(x)である。ω(x)≡¬x(x)は定義であるからこれは排除されないが、この文は、ω(x)≡¬x(x)という顔を持つのと同時に、単なるx(x)の顔を持つようになる。したがってこの文はω(x)≡¬x(x)という一つの論理式では表現できない文となる。
つまり、この種の繰り返し文をそれ自体、矛盾とみることで、対応説的見方がもたらす「この文は¬x(x)である、したがってこの文はω(x)である」という断定を行えないようにして、その先、xにωを代入することによって起こる矛盾を回避したということである。それはその代入操作から生じる矛盾を、出発点である命題自身に二重化として帰したということである。
真理の対応説と整合説の両者を採用する直観主義論理においては、主語述語の繰り返し文のうち、「『犬である』は犬である」の類は矛盾命題といえる。しかしながらこれを「矛盾」とすることは、あくまでも古典論理の見方に立った物言いであり、実際にこの種の命題は、対応説的には偽でありながら整合説的には常に真であるという量子論的事態にも似た状況にあるというのが事実であって、この事態を古典論理は片側からしか捉えていない論理であるということができるのかもしれない。
ところで、先のe言明
「『犬である』は犬である」は証明できない――e
は、これを同語反復に読んで、
「『犬である』は犬である」は何事も語っていない――e
と読むとき、その意味が理解できるものになる。確かに、同語反復すなわちトートロジーは事実に関して何事も語らない言明である(『論理学』p.38 参照)。「明日は晴れか晴れではない」という主張は同語反復型ではないトートロジーだが、やはり明日に関して何も語っていない。
そして「何事も語らない」ということは、事態は「不明」であり「証明できない」ということでもある。それゆえ、直観主義論理が、¬に「不」という新たな意味を加えたということは、繰り返し文を何事も語っていない同語反復として読むことを加えたこととして解せるのである。
このように捉えると、ラッセルパラドクス回避のために直観主義論理が¬記号へ「不」を追加したという解釈は、同じく直観主義論理が、自己言及文および一般文に対して「対応説的見方」の他に「整合説的見方」すなわち、同語反復読みを許容したとする解釈と同じ関係にあるといえる。この理解も、ラッセルパラドクス回避のために直観主義論理が何を行ったかについての解釈可能性の一つとしておきたい。