| 第二部 信仰と理性論 | 星加弘文 |
(1) 認識史分析とは論理記号を取り去る操作のこと
「認識史分析」（野矢茂樹『論理学』p.178以下）は、直観主義論理の論理式が妥当式（Hard study 5-2-3参照）であるかどうかを調べる手続きである。古典論理には「真理値分析」があるが（Easy Study 2-2）、両者には方法と達成できることに違いがある。
古典論理の真理値分析では、論理式の値はその式を構成する原子命題の真理値の組み合わせすべてについて計算される。
例えば、2命題Ｐ、Ｑの論理式の真理値は4行の真理表で計算されるが、これは原子命題ＰおよびＱの真偽の4通りの組み合わせすべてにおける真理値を計算しているということである。その上で、その式がトートロジーであるかどうかは、4行すべての真理値が1であるか否かによって知られる。
一方、直観主義論理の認識史分析は、原子命題の真偽の組み合わせごとにその「証明値」を明らかにするものではなく、ただその式が妥当式であるか否かだけを判別する手続きである。
認識史分析は、与えられた論理式が証明されないものと仮定した上で、意味論規則を適用して論理記号を取り去っていき、その行く末が矛盾に至るかどうかを見ることによって行われる。
この操作は式変形の複数の道筋を生じさせるが、いずれの道筋もすべて矛盾に行き着くのであれば、初めにその式を証明できないと仮定したことが誤りであったことが結論される。
「証明されない」という初めの仮定は、その式を意味論から導出できない式、つまり非妥当式と仮定したということなので、その式に対して意味論の規則を適用した結果が矛盾を起こすのであれば、もとの論理式は意味論から導出できる式、つまり妥当式であったということになる。
したがってここでは「不証明（⊮）」と「矛盾」について二重否定除去が行われている。直観主義論理では「￢Ａを仮定して矛盾が出るときＡを導出してよい」という否定除去型の背理法、つまり二重否定除去が認められないことはHard study 5-2-2以下で見た通りである。
認識史分析においてそれが許されているのは、Hard study 5-3-2後半部分で確認した通り、直観主義論理意味論では⊩と⊮が論理的真理としての排中律を構成する仕方で用いられていることによる。証明／不証明を意味する⊩と⊮を排中律として使えるのであれば、排中律と同義である二重否定除去則と否定除去型背理法も使えるということである。
この認識史分析の方法は、一般にタブロー法と呼ばれるもので、放送大学のあるテキストは、タブローについて「命題を一定の規則に従ってより単純な命題へと分解する」方法として紹介している。
与えられた論理式に対して、その式に含まれる4つの論理記号∧、∨、⊃、￢を意味論の規則に従って取り去っていき、分子命題から原子命題レベルでの証明／不証明の状態へと式を還元するのがタブロー法である。『論理学』p.182に「樹形図」で示されている直観主義論理の認識史分析はこれを表している。
つまり認識史分析は、Easy study 5-2-1に掲載した直観主義論理意味論Ⅱ(2)～(5)における→方向の規則だけを使用するものである。この意味論は、左辺から右辺へは論理記号の除去について述べ、右辺から左辺へは論理記号の導入を述べている。
意味論が論理記号の除去と導入の規則を述べるものであるということは、論理記号なしの言明と論理記号ありの言明を結びつけているということであるから、それは論理記号と日常言語の対応付けを行っていることといえる。論理体系と世界の対応付けといってもよい。このことがこの規則が「意味論」と呼ばれる所以である。「意味」とは、通常、2つの項の対応付けとして理解されるものだからである。
(2) 現状分析と将来分析
（以下を読むためには、野矢茂樹『論理学』の参照が必要）
認識史分析は論理記号の除去に関わるものなので、証明済の∧、∨、⊃、￢各式の除去と、不証明の∧、∨、⊃、￢各式の除去の8種類の操作を行う。
ここで論理記号の証明済、不証明というのは、分子式の一番「外」にあって働いている論理記号が、その分子式全体の証明／不証明を決定している状態のことで、認識史分析の初めに式全体を不証明と仮定することから始まり、分解された式においてもこの事態が次々に生じていくことになる。
『論理学』の中では、証明済の∧、∨、⊃、￢と不証明の∧、∨の除去操作を「現状分析」、不証明の⊃、￢の除去操作を「将来分析」と呼んでいる。 認識史分析を行うためには『論理学』に書かれている手順を機械的に実行すればよく、特に「現状分析」と「将来分析」についての正確な理解が必要であるわけではない。しかし私としては「現状分析」と「将来分析」を分ける基準が何であるのかが気になるところである。
直観主義論理意味論Ⅱでは、(2)∧、(3)∨がα期のみの言及であるのに対し、(4)⊃、(5)￢にはβ期への言及がある。そこで、意味論の片側規則（除去規則のみ）といえる認識史分析において、⊃と￢が「将来分析」と呼ばれることは一見自然なことのように感じられる。
しかし、不証明である⊃と￢だけが将来分析と呼ばれ、証明済の⊃と￢については現状分析と呼ばれているので、上のように単純に納得してはいけないようである。
意味論が記されている頁に遡ると『論理学』p.172に(4)⊃、(5)￢に関して次の記述がある。
道元「（(4)と(5)の右辺に）『αRβなるすべてのβに対して』という条件（が付いているの）はなぜかな。」
野矢「これは基本的に(2)や(3)にもついているはずのものです。」
ここでの説明によると、∧と∨についてもβ期への言及がなされているのが意味論Ⅱ(2)、(3)の本来の状態であるということである。しかしそうすると、∧と∨についても将来分析があってよいことになり、意味論の中で⊃と￢にβ期への言及があることが将来分析と呼ぶことの理由だとする先の見方はさらに成り立たないものとなる。
混乱してきたので視点を変えてみる。そもそも「将来分析」とは何を述べたものなのだろうか。
不証明の￢の除去操作を見てみる。（以下『論理学』に倣って証明済を＋、不証明を－で表わす。）
－￢の将来分析 <α>－￢Ａ ―― <β>＋Ａ
これはα期で不証明である￢Ａについて、β期で証明済Ａが言えるということである。
Hard study 5-3-1「直観主義論理の￢Ｐの証明表2」を見ると、<α>－￢Ｐとなっているのは認識史11と01であり、これらはいずれも~βでは＋Ｐとなっている。
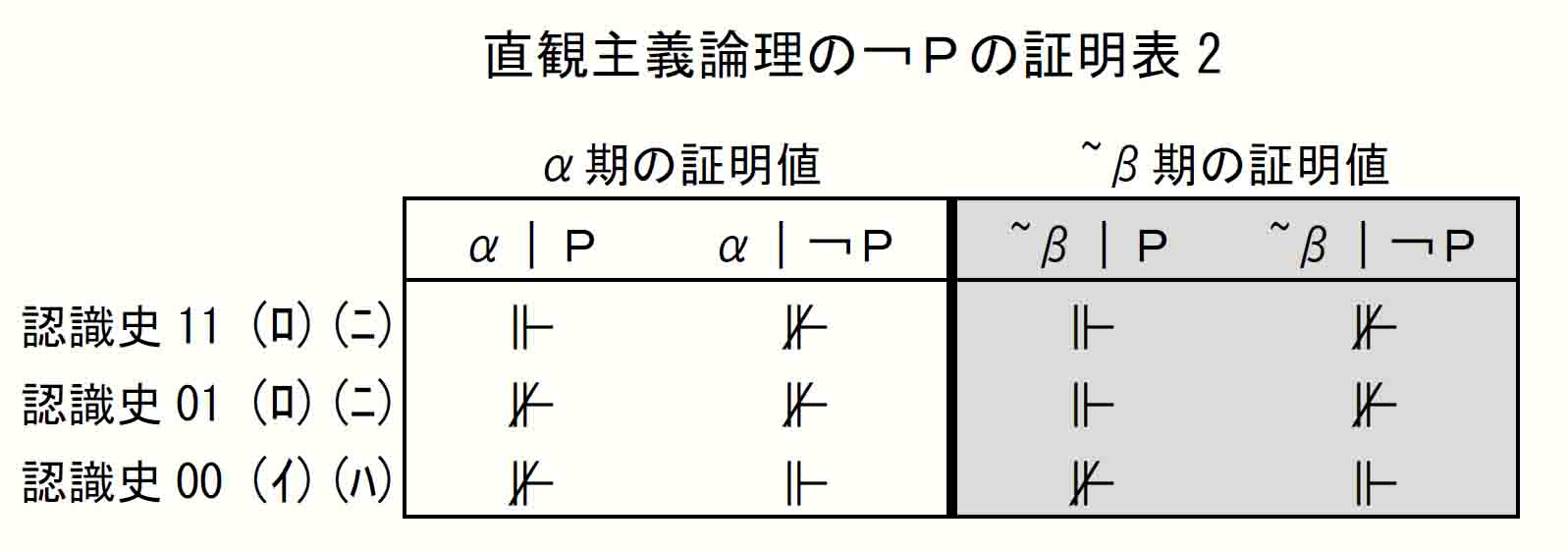
つまりα期で不証明である￢Ｐは、~βでは必ず証明済Ｐとなっていて、上の「－￢の将来分析」と合致する。
不証明の⊃の除去操作は以下である。
－⊃の将来分析 <α>－(Ａ⊃Ｂ) ―― <β>＋Ａ,－Ｂ
これはα期で不証明であるＡ⊃Ｂでは、β期に証明済Ａと不証明Ｂの同時存在があるということである。この事態を意味論(4)で見ると以下である。
意味論Ⅱ(4)→方向裏（不証明の⊃の除去則）
α⊮Ａ⊃Ｂのとき、あるβで⊩Ａかつ⊮Ｂ。
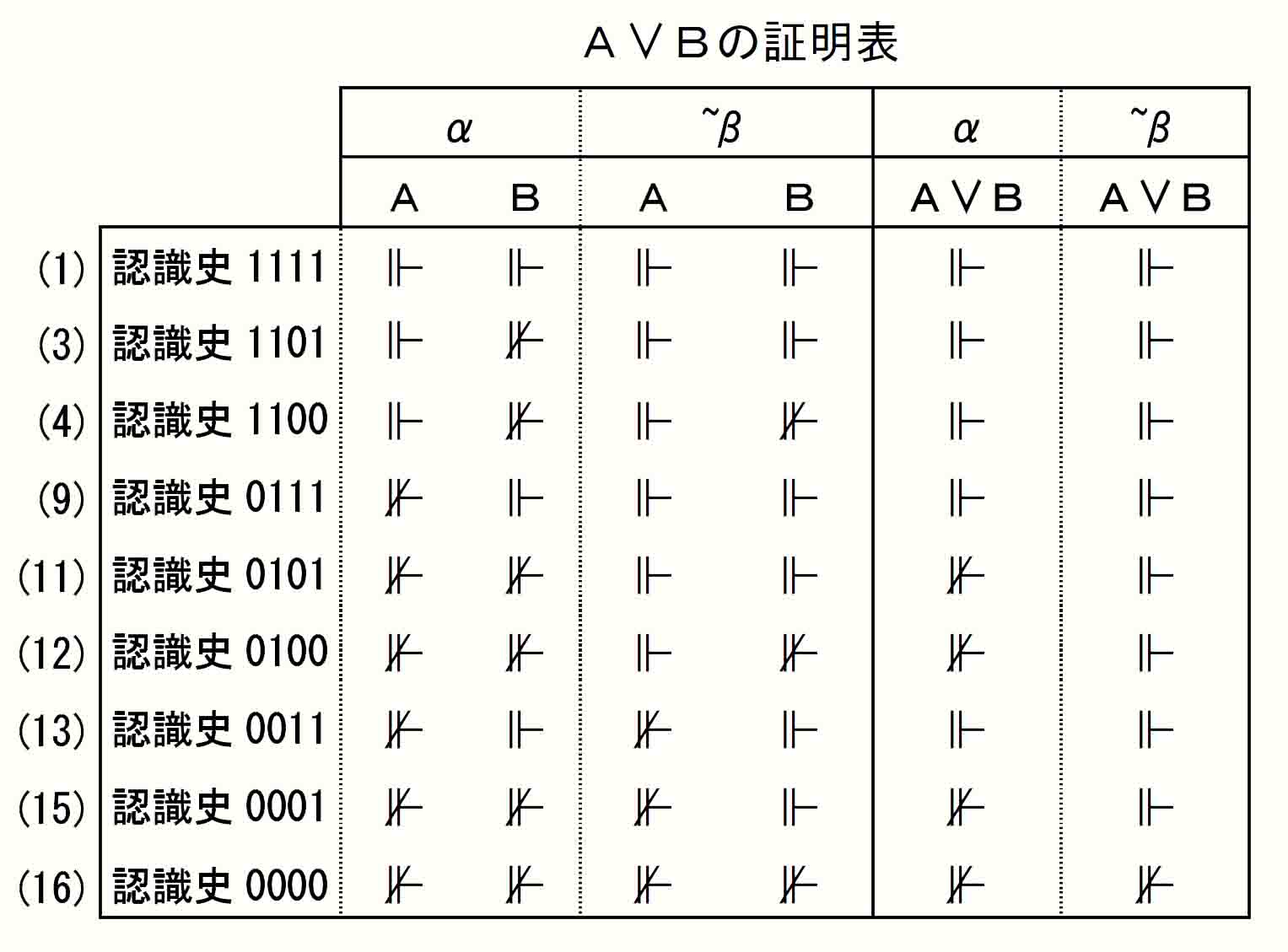
次節の「Ａ⊃Ｂの証明表」で確認できるが、α期でＡ⊃Ｂが不証明であるのは、認識史1101、1100、0100で、⊩Ａかつ⊮Ｂの事態は認識史1101ではαで起きており、1100ではαと~βで起きており、0100では~βで起きている。
つまり「－⊃の将来分析」に書かれている<β>は「あるβ」のことであり、そう解すれば－⊃の将来分析と意味論Ⅱ(4)→方向裏は一致する。
すると、－￢と－⊃を合わせて、いずれもα期での不証明状態から「あるβ」については確実なこと――－￢では「Ａが証明済」、－⊃では「Ａが証明済かつＢが不証明」――が言えるということである。この「あるβで確実なことが言える」、言いかえるとαにおける－￢と－⊃は、あるβにおいて確実な式変換すなわち論理記号の除去ができるということである。したがってこの操作をβに因んで「将来分析」と呼ぶことは適切であるように思えてくる。
しかし「あるβ」で確実なことが言える除去操作を「将来分析」と呼ぶというのであれば、次の事態はどうだろうか。
＋∧の現状分析 <α>＋(Ａ∧Ｂ) ―― <α>＋(Ａ∧Ｂ),＋Ａ,＋Ｂ
これも次節の「Ａ∧Ｂの証明表」で確認するのがよいが、αでＡ∧Ｂが証明されている唯一の認識史1111においては、αだけでなく~βでも＋Ａ,＋Ｂが成り立っている。したがってここではβで、しかも「すべてのβ」で確実なことが言える。
「＋∨の現状分析」も同様である。
＋∨の現状分析 <α>＋(Ａ∨Ｂ) ―┬― <α>＋(Ａ∨Ｂ),＋Ａ
└― <α>＋(Ａ∨Ｂ),＋Ｂ
認識史分析が枝分かれしているのは、＋∨の除去では、論理記号を取り去った還元状態に二つのあり方があるということで、逆を言えば、元の論理式は、その二つの状態から元の式を取り去った上でも、それらのいずれからでも作成できるということである。（『論理学』p.167 LIP規則7「ＡからＡ∨Ｂを導出してよい」「ＢからＡ∨Ｂを導出してよい」）
αでＡ∨Ｂが証明済である認識史は1111、1101、1100、0111、0011だが、これらの認識史では、αでも~βでも「Ａが証明済かまたはＢが証明済」が成立している。ここでも認識史分析が示す事態は「すべてのβ」で成立している。
そしてこのことは、∧と∨にも本来は「『すべてのβ』が付いている」という『論理学』の説明とも符合することである。
したがって「あるβ」で確実なことが言える除去操作を「将来分析」と呼ぶのであれば、「すべてのβ」で確実な事態が成り立っている「＋∧の現状分析」と「＋∨の現状分析」を将来分析と呼ばないというのは辻褄が合わないことになってくるのである。
こうしたことから私は「現状分析」と「将来分析」の基準に相当の期間「嵌まった」が、これをもたらした要因は、先に挙げた『論理学』p.172の記述が不十分あるいは適切ではないことにあるといえる。
そこでは「すべてのβに対して」という条件は(2)や(3)にも基本的についているはずのもの、と書かれており、続けて「(2)や(3)ではその条件を書いておかなくても、Ⅱ(1)によってβでの証明値がαから維持されるので書いておく必要がない」旨が書かれている。
このため私は数年もの間（！）、例えば、意味論Ⅱ(2)←方向を
意味論Ⅱ(2) ←方向
αで⊩Ａかつ⊩Ｂのとき、αで⊩Ａ∧Ｂ
という正規の規則のままではなく、
すべてのβで⊩Ａかつ⊩Ｂのとき、αで⊩Ａ∧Ｂ
と読むようにしていた。
正規の規則が、α⊩Ａ∧Ｂであるための条件を、ただα期のＡが証明済であり、かつα期のＢが証明済であることとしているのに対し、「すべてのβ」に読み替えた方は、「すべてのβ」つまりα期と~β期のいずれにおいてもＡとＢが証明済であることが条件となっており、α⊩Ａ∧Ｂであるための条件が厳しくなっている。
ただしここにはいくらかややこしい事情があり、この条件の厳しさは見かけ上のものとも言え、「すべてのβで⊩Ａかつ⊩Ｂのとき」というのは、Ⅱ(1)により「αで⊩Ａかつ⊩Ｂのとき」と同じことなので、実際には「すべてのβ」と読み替えることで条件が厳しくなっているわけではない。
同様に、意味論Ⅱ(2)←方向裏では次のようである。
意味論Ⅱ(2) ←方向裏
αで⊮Ａまたは⊮Ｂのとき、αで⊮Ａ∧Ｂ
が正規の規則だが、元の意味論Ⅱ(2)の右辺に「すべてのβ」を持ち込むと
あるβで⊮Ａまたは⊮Ｂのとき、αで⊮Ａ∧Ｂ
となり、αで⊮Ａ∧Ｂであるための条件が、「αまたは~βのいずれかで」となることで、正規の規則「αで」よりも条件が緩くなる。
ただしこちらも次節に挙げた「Ａ∧Ｂの証明表」で調べてみると、α期で⊮Ａ∧Ｂとなっている認識史では、みなα期の原子命題の状況によりそれが成立しているので、実際には正規の規則が緩くなった状態（~β期の原子命題の状況によってのみα⊮Ａ∧Ｂが成立している状態）が存在するわけではない。
意味論Ⅱ(3)についても同様の事態であるので、(2)∧と(3)∨にも「基本的に『すべてのβで』が付いている」とする『論理学』の説明が不適切というのではないのかもしれない。
しかしいずれにせよ、「すべてのβ」で認識史分析の規則が成立する＋∧と＋∨が「将来分析」と呼ばれていないことへの疑問は残ったままである。確実な式変換が「あるβ」で行えることを「将来分析」と呼ぶのであれば、「あるβ」を含んでいる「すべてのβ」で確実な式変換ができることを「将来分析」と呼ばないことの理由が分からない。
では、どのように理解すべきなのか。
まず「将来分析」とは論理記号の除去操作において、β期について確実なことを言うことができる操作のことである、という理解は保つ。すると、βについて確実なことが言える＋∧と＋∨については、理屈としてはとりあえずこれを将来分析の部類に含めてよいとしなければならない。
ところで、将来分析というのは将来期についての言及であるため、併存する不証明の論理式を引き継げないという規則がある。不証明である式が将来期において不証明のまま残るとは限らないからである。
したがって、理屈上、将来分析と呼べる事態があったとしても、それが「すべてのβ」すなわちα期でも実現されている将来分析である場合には、これをわざわざ不証明式を失う将来期での分析として行うのではなく、現状分析としてα期での式操作にしておくのが適切ということになる。
確実なことが少なくなる将来よりも、不証明式とはいえ、その情報を保持し、その式についても認識史分析が行える現在の方が豊かであるという理解である。このためα期で確実なことが言える＋∧と＋∨は現在期において分析を行う現状分析とし、将来分析とはしないのである。
この事情から「すべてのβ」すなわちα期についても確実なことが言える除去操作は「現状分析」であり、「あるβ」についてだけ確実なことが言える除去操作が「将来分析」と呼ばれているということである。
したがって、意味論Ⅱ(2)(3)について「本来は『すべてのβ』という条件がついているべき」とする『論理学』の記述が上の混乱の根本的な要因であったわけではなく（きっかけではあったが）、むしろ「すべてのβ」で可能な式変換と、「あるβ」においてだけ可能となる式変換の区別を明確に理解する機会を与えてくれた記述であったともいえる。
ただし、『論理学』のこの記述には別の基本的な問題があり、やはりそのことが、本来は混乱を招くような場面ではないところに要らぬ混乱をもたらす要因となったことは否定できない。
後節で見る、直観主義論理のもう一つの意味論である「ハイティング代数」の定義では、順序集合から束（そく）が定義されるところで∧と∨が定義される。その後、∧を使って⊃が定義され、⊃から￢が定義される。
一方、古典論理の意味論である「ブール代数」においても、∧と∨は順序集合から束が定義されるところで定義される。∧と∨の定義のされ方は「ハイティング代数」と「ブール代数」で同じなのである。これは∧と∨に関して、直観主義論理と古典論理が同じ定義を持つことを示すものである。
つまり、意味論Ⅱ(2)、(3)の右辺に「すべてのβ」がないのは、直観主義論理の∧と∨の性質が古典論理と同様に無時間的なものであって、クリプキ意味論の「期」概念とは無縁だからなのである。
(2)∧と(3)∨がα期の言及にとどまるのは、分子式の証明値が時間的概念なしに、単に同期の原子式の証明値から決定してよいことを示している。それゆえ(2)∧と(3)∨において「β」はα期のための条件なのではない。ここにβの言及がないのは、Ⅱ(1)によって証明値が保証されるからではなく、αRβという期概念が適用されないからなのである。
このことは、~βの∧と∨の分子式についても、同期すなわち~βの原子式の証明値から決定できることをいうものでもある。
一方、意味論Ⅱ(4)⊃、(5)￢の右辺で「すべてのβ」が言及されているのは、←方向に読むときに、左辺のαでの⊃や￢の論理式の証明値は同期αの原子式の証明値だけからは決定できず、将来期~βの原子式の状態までをみて初めて決定できることをいうものであり、すなわちこれはα期のための条件なのである。
したがって、∧と∨については、「本来は『すべてのβ』という条件がついているべき」とするのは適切ではなく、古典論理との共通性、無時間性を述べて、「すべてのβ」を必要とする⊃、￢との違いを示すことが適切な説明であったと考える。
さて、認識史分析とは現状分析がαにとどまる操作で、将来分析がβに期を進めての操作という印象を持つが、そうすると「現状」「将来」の名称から来る先の混乱を招きやすくなるので、以下のように理解するのがよいだろう。
「現状／将来」という意味から見れば、現状分析も将来分析も単なる現状における式変換つまり「現状分析」と呼ばれるべきものである。ただし、－⊃と－￢では、将来期の証明値をいわば盗み見たうえでの式変換となるため、それは将来を現在の条件とすることとなって、変換対象以外の式の将来期での不確かさを現在に背負うことになる。このため－⊃と－￢の式変換では、変換対象以外の現状にある不証明式は現状において捨てられなければならないが、この、将来期を起因として現状で不証明式を捨てた状態は、期が一つ進んだ状態と見なすことができるので、これを「将来分析」と呼ぶということである。