| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (12)
Hard study 5-2-3 「排中律の拒否」と意味論間の矛盾
さて、意味論との矛盾があるように見えるのは、前段の二重否定除去則の拒否だけではない。排中律もまた、定理としては拒否されていながら、意味論においては認められている面がある。こちらについては同書にも触れられているので引用してみよう。
論題25
道元「すると『α⊩Ｐであるか、α⊮Ｐであるかどちらか』なのかね。だがこれはまさに直観主義が拒否した排中律そのものじゃないのか。」
野矢「実になんと言うか、…いや、これもまた、説明不足でしたかね。」（p.175）
これについての巻末解説では「排中律は無限に関係する場合に問題となるが、命題の証明、不証明は無限に関わるものではないので排中律が用いられていて問題はない」と説明されている。
しかしこの説明はよく分からない。直観主義論理を適用した事象が有限であった場合、排中律を定理として適用してよいということなのだろうか。先に挙げられていた「勇気」は無限に関係しているので排中律では論じられないということなのか。しかし「勇気」が無限に関係しているようには思えない。
確かに、排中律が適用できないと考えられる確実な例であるπの小数列は無限であり、排中律の適用、不適用の何らかの境界として無限が関係しているということは言えそうである。
しかしそのことが、直観主義論理意味論において「α⊩Ｐであるか、α⊮Ｐであるかどちらか」という定義が機能していることの本当の理由なのだろうか。なお不明瞭だが、ともかく排中律に関しては、直観主義論理の意味論がそれを含んでいることを確かなこととして受け止めなければならない。
さてそういうことならば、次のように考えてすっきりさせてしまうのはどうだろうか。
すなわち、直観主義論理が拒否している排中律と二重否定除去則は、その意味論においてはいずれも採用されているのであって、公理を定める段階で初めて拒否されている……。意味論に対し、公理から出発するいわゆる「記号論理学」のことを「構文論」というが、実はこの構文論が意味論規則に対し公認／非公認の判断を行っており、その判断がその論理の性質を決定づけているのである…。それゆえ論理の出発点としての公理群を定める構文論が偉大なのである……。
しかしながらこの理解はまったくの早合点であって正しくない。というのは、Ｐ∨￢Ｐ、￢￢Ｐ⊃Ｐのいずれも、直観主義論理の意味論規定からの推論によって、論理的真理ではないことが証明されるからである。これは意味論自体に、Ｐ∨￢Ｐ、￢￢Ｐ⊃Ｐを公理として認めない規則が仕込まれていることを示している。
そうするとこれまでの事態はさらに理解し難いものとなるようにも思えるが、とりあえず理解できるところから確認していくことにしよう。同書に掲載されている、Ｐ∨￢Ｐ、￢￢Ｐ⊃Ｐが論理的真理ではないことの証明を確認してみよう。
以下の証明では「論理的真理」についての理解が必要となるので、あらためてこれを思い出しておこう。論理的真理については、Easy study 2-2「￢Ｐの真理表」から「Ｐ∨￢Ｐの真理表」にかけて説明している。
確認すると、論理的真理とは「元の命題の真偽に関係なく常に真となる言明」のことをいう。例えば、前件肯定式(Ａ⊃Ｂ)∧Ｂ⊃Ｂが論理的真理であるかどうかを調べるには、ＡとＢの4通りの真偽の組み合せからなる4行の真理表を作る。
そしてその1行ごとに、古典論理の意味論である「⊃の真理表」と「∧の真理表」を使って真理値を計算してゆき、最終的に(Ａ⊃Ｂ)∧Ｂ⊃Ｂの真理値を得る。その結果、4行すべてに1が入るならば、前件肯定式の論理的真理であることが確認されるということである。そして古典命題論理の場合、このような論理的真理の式のことを「トートロジー」と呼ぶのであった。
これから見ようとする直観主義命題論理の場合も同じように理解できる。ただし直観主義論理では、元の命題がＡ、Ｂ2個の場合、例えばＡ⊃Ｂについて調べる場合、それぞれにα期での証明状態とβ期での証明状態があるため合計16行からなる「証明表」ができることになる。（ただしαで証明済、βで未証明となるありえない認識史の行を排除すると9行となる。）
ここで調べようとしているＰ∨￢Ｐ、￢￢Ｐ⊃Ｐの場合は、いずれも元の命題が1個なので4行の「証明表」となる。Ｐ∨￢Ｐについて作成すると以下のようである。
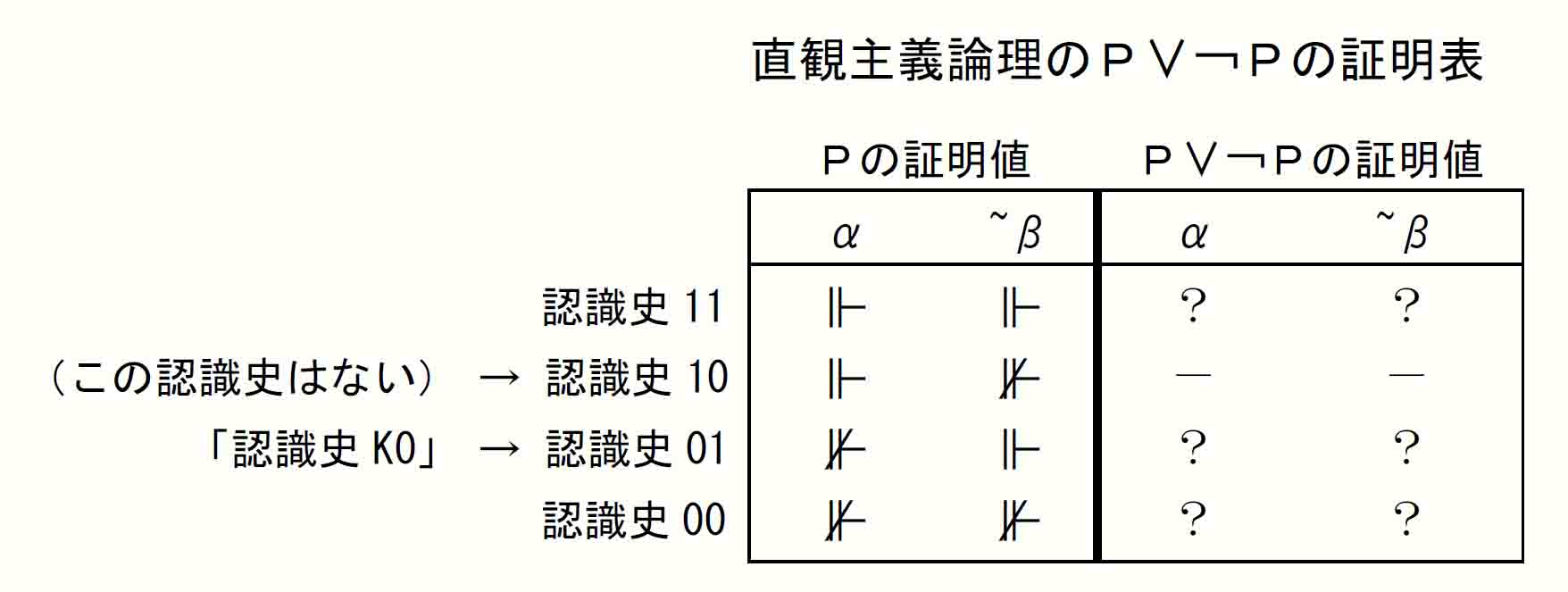
「Ｐの証明値」の各行が命題Ｐについての認識史であり、便宜的に上から認識史11、10、01、00と名づけておく。ただし認識史10は、証明された命題が後に不証明となることをいうものなので、直観主義論理の意味論Ⅱ(1)により除外される。
なお、βはαを含む後続期であるため、認識史01をα⊮Ｐ、すべてのβについてβ⊩Ｐとすると矛盾となり、そのための処理が煩雑になるので、α期を除いた後続期としての~β（チルダベータ）を用いる。
ここでα期、~β期のすべてのＰ∨￢Ｐの証明値のところ（上では？マークが入っているところ）に⊩（証明済）が入るならば、この論理式は直観主義論理における論理的真理ということになる。
古典論理のＰ∨￢Ｐの真理表にすべて1が入ることと同じで、元のＰの証明値が何であれ、Ｐ∨￢Ｐのすべての認識史における証明値が⊩であるなら、この式は論理的真理の式なのである。なお、直観主義論理での論理的真理の式は「妥当式」と呼ばれる。
以上を踏まえた上で同書の証明を見ていこう。
Ｐ∨￢Ｐが妥当式かどうかを調べる。目的は直観主義論理のＰ∨￢Ｐが妥当式ではないことを示すことにあるので、上の実質的に3行2列、計6個からなる証明表の「？」のどこかに「⊮」が入ることが示されればそれが証明できたことになる。
そこで『論理学』では、認識史01の行を調べよ、ということになっている。同書ではこれを「認識史K0」としている。（p.176「② 認識史モデルK0」でＰについてのα0とα1の証明値が「認識史01」相当）
以下、同書の証明を補足しながら辿ってみる。
なお、以下の証明で「～のとき」「～ならば」という語は「条件法」ではなく「同値」の意味で使用している。詳細は注参照。
■認識史01α期のＰ∨￢Ｐの証明値（p.176(d)）
意味論規定Ⅱ(3)←方向により､α⊩Ｐまたはα⊩￢Ｐならば､α⊩Ｐ∨￢Ｐ……(1)
もし(1)の前件が成立しなければ後件も成立せず、α⊮Ｐ∨￢Ｐとなる。
(1)の前件は選言なので「または」の前後両方の否定が成立すれば、前件が成立しないことになる。以下、α⊮Ｐであり、かつα⊮￢Ｐであることを確認する。
認識史01であるからα⊮Ｐ……(2)
意味論規定Ⅱ(5)←方向により、すべてのβで⊮Ｐならばαで⊩￢Ｐ
すなわち、α⊮Ｐかつ~β⊮Ｐの認識史のとき、αで⊩￢Ｐ
そして認識史01はα⊮Ｐかつ~β⊩Ｐなので、αでは⊩￢Ｐとはならない。
すなわち、αでは⊮￢Ｐ…(3)
(2)と(3)により、(1)の前件が成立しないことが確認された。
ゆえに(1)の後件は成立しない。
すなわちα⊮Ｐ∨￢Ｐ
したがってＰ∨￢Ｐは妥当式ではない。
続いて、￢￢Ｐ⊃Ｐについて調べる。こちらも同書の証明を補足しながら認識史01の値を調べてみる。
■認識史01α期の￢￢Ｐ⊃Ｐの証明値（p.178 問題79）
認識史01では~β⊩Ｐなので、Ⅱ(5)←方向裏により、α⊮￢Ｐ……(1)
また~β⊩Ｐであるから、~β⊮￢Ｐ……(2)
(1)、(2)と、Ⅱ(5)←方向により、α⊩￢(￢Ｐ)……(3)
認識史01ではα⊮Ｐ……(4)
⊃で結ばれた条件式は、前件が真、後件が偽のとき偽であるから、(3)と(4)によりα期の￢￢Ｐ⊃Ｐは偽。
すなわちα⊮￢￢Ｐ⊃Ｐ
したがって￢￢Ｐ⊃Ｐは妥当式ではない。
ということで、排中律も二重否定除去則も妥当式ではないことが、意味論から導かれた。
これで意味論そのものに排中律拒否、二重否定除去則拒否という直観主義論理の特質が仕込まれていることがはっきりしたので、先の「意味論で承認されている規則が構文論で拒否される」という見方が見当違いであることは確認できた。