| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (5)
Easy Study 2 古典的演繹――整合説の応用1
2-1 前件肯定式推論
「理性の内訳表」(Section 3)の横軸に配した「実在論・解釈学」「古典的演繹」「構成主義」は、いずれも前節に述べた「真理の整合説」を発展させたものである。
真理の整合説を基本とする思惟体系は、模式的に「AならばBである」という「前件Aと後件B」からなる説として表現することができる。この「ならば」の部分はときに長い演繹の連鎖となる場合があり、また前件Aは「ならば」という条件接続詞が示すとおり仮定による設定である。
つまり、この整合説的体系は、前件Aが「仮に真である」という設定に基づいた上で、その後の論証の整合性だけを問題にしたものである。先の例でいえば「背の高い人間は人間である」とは、「仮にあるものが背の高い人間であるならそれは人間である」ということであって、それ以上の主張、例えば「背の高い人間」が実際に存在するといった主張を含むものではない。前件Aに該当するものが世界に実在するかどうかは、論理によってではなく観察によって初めて決定できることである。
さてそこで、前件Aを仮定としてではなく、前節で述べた「真理の対応説」において保証されるような一個の真理として置くことができれば、前件Aから始まる整合説的体系は、その全体が真理となるはずと考えられる。始点は真理の対応説、それ以後は真理の整合説によって保証されるからである。カントも含め近代以前の哲学の体系は、このようなものを目ざして考えられてきた。
デカルトの『省察』に述べられている有名な「方法的懐疑」によって行われたのは、この最初に置かれるべき確実な真理としての前件Aの探求であったといえる。彼は思惟の確実な出発点を求め、そのため疑いえるものをすべて疑うという方法をとり、そこで、いま自分が疑いえるものを疑おうとしているそのこと自体は疑えないという洞察をえて「われ思うゆえにわれあり」という最初の命題を導いたというわけである。
この後、デカルトは神と世界の論証に進み、体系哲学を完成させることになる。外界や神の存在よりも、それまで誤謬の源泉とみられてきた観念的意識を第一の確実な原理とするというデカルトの考え方は、近代哲学の端緒となって以後の哲学に大きな変革をもたらした。しかし、確実な出発点を初めに設定するという演繹構造そのものは、それ以前の思想体系を踏襲したものだったのである。
中世におけるキリスト教の哲学、いわゆるスコラ哲学とか形而上学と呼ばれる体系は、これと同じ演繹構造に基づいている。トマス・アクィナスは「神学は学問であるか」という問いに次のように答えている。
――二種類の学問がある。一つは人間の自然的知性によって明らかとなった基本命題から出発するもので数学、幾何学などである。もう一つはより上位の知性、すなわち神の知性が明らかにした基本命題から出発するものである。神学は後者であり、すなわち神学は学である。
ここには、神学および一般学のいずれにおいても、まず確実とみなされる基本命題があり、そこから体系が築かれるという学問観が明瞭に見てとれる。
18世紀になって、カントの超越論哲学は中世型の古い形而上学を完全に瓦解させるに至ったが、しかしそれは、形而上学の出発点である聖書の基本命題を不確実とみることによったのではなく、出発点以後の論理の方を問題にすることによって行われた。形而上すなわち経験を超えた世界のことがらを、有限である人間理性の論理において述べることがはたして可能なのか、理性にその資格があるのかをカントは問題とする。
そして、理性にその資格がないことを論証するために、彼は、理性の由来についての根拠づけを、デカルトの「われ思う」に準ずる「純粋統覚」という主観能力に求め、これを外界認識の第一原理として提出する。それゆえカントもまた、理論の出発点となる確実な真理の発見、すなわち「基礎づけ」に余念がなかったわけである。
これらの古い演繹体系は、論理学の前件肯定式(A⊃B)∧A「AならばB、かつAである」
このような前件肯定式推論における結論Bが真理性を保つことは、常識においても理解されることだが、後に扱う後件肯定式推論との比較のために、ここで真理表を使ってその点を確認しておこう。
いま、 A⊃B「AならばB」を述べられた理論とすると、理論仮定Aと理論帰結Bのそれぞれの真偽に応じて4通りの組み合せが考えられる(次表1列目、2列目)。
このとき理論「A⊃B」自体の真理値(真であるか偽であるか)が次表3列目のとおりに与えられることは命題論理の一般的な規則であり、論理学の入門書で確認することができる。
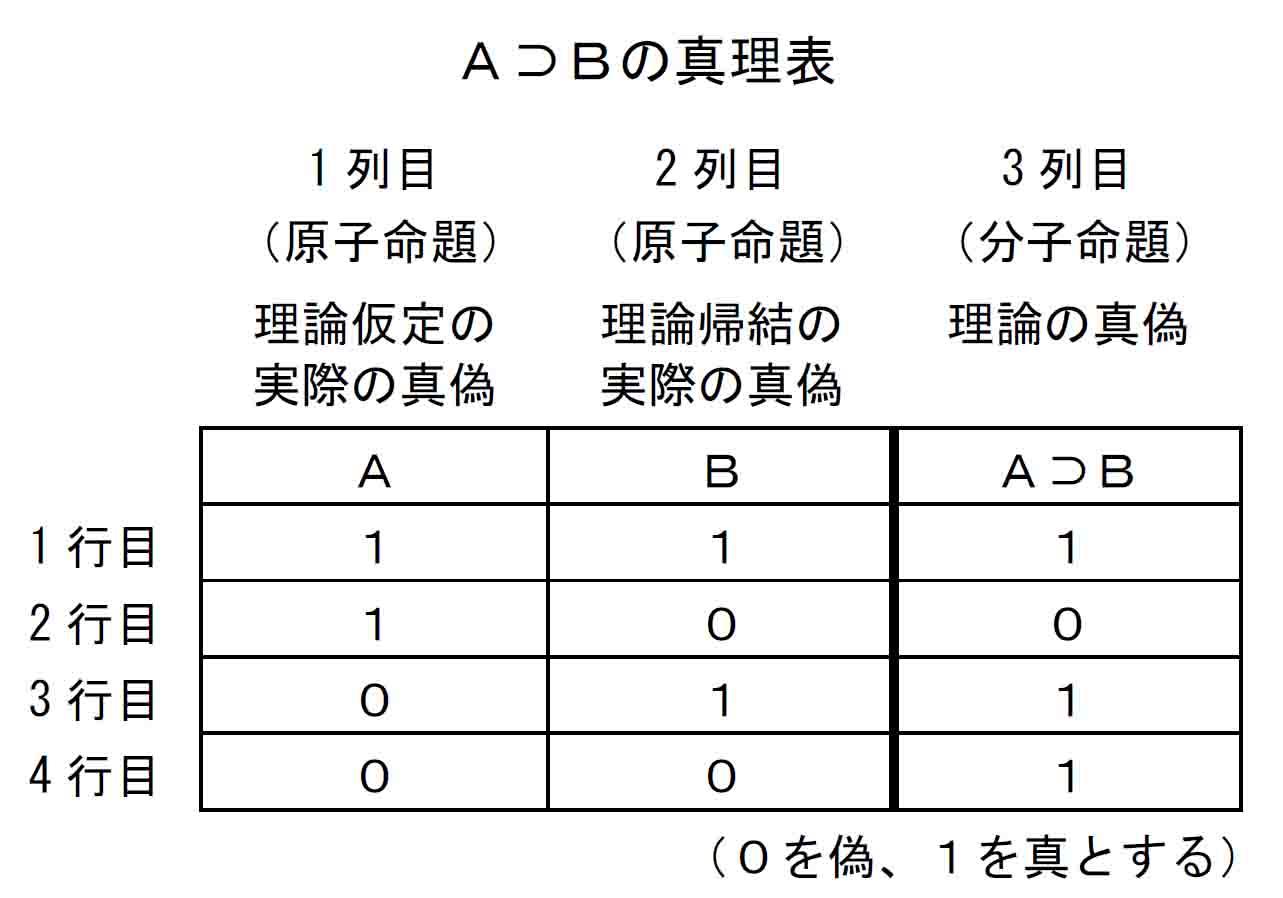
以下は、野矢茂樹『論理学』
Aを「明日は晴れる」という命題、Bを「動物園に行く」という命題とする。ここで、ありえる事態が4通り考えられる。いいかえれば、この4通りが、世界においてありえる事態のすべてであり、そのことが1列目と2列目の値の組み合せで表現されている。
1行目のA、Bは1、1、すなわち真、真であるから、当日晴れて動物園に行ったという事態を表している。同様に2行目は、当日晴れたが動物園に行かなかったという事態を表している。3行目は、当日雨降りだったが動物園には行ったという事態を示し、4行目は、当日雨降りで動物園にも行かなかったことを示している。
さて、実は前日、父親は子どもに「明日晴れたら動物園に行く」という約束をしていた。つまり、この父親は子どもに「AならばBだ」という一つの論理的な命題を宣言していたわけである。
当日になり、晴れていて、そして動物園に行ったとすると父親の約束は果たされたわけなので、父親の言明は本当だったことになる。つまり父の宣言「A⊃B」はこのとき真の値を持つことになる。これが1行目の3列目(「A⊃B」列)の1で表現されていることである。
2行目の事態を見てみると、2行目では、当日晴れたのに動物園には行かなかった。この場合、父親は「明日晴れたら動物園に行く」という約束を破ったことになり、前日の「AならばBだ」という宣言は嘘だったことになりA⊃Bは偽である。したがって2行目の3列目には0が与えられる。
さて3行目は、当日はあいにく雨、しかし動物園には行ったことを表している。この場合、父親は嘘つきになるのだろうか、それとも嘘つきではないとしてよいのだろうか。命題論理の一般的な条件法の定義では、仮定Aが偽である場合、条件命題A⊃Bの全体は真とされる。これは次のように理解できる。
確かに父親は「明日晴れたら云々」と言ったが、晴れなかった場合のことについては何も言っていない。もし「明日晴れた場合に限り連れて行く」と言っていたならば、雨なのに出かけるのはことば通りではないというということになるが、単に「晴れたら」と言っているだけの場合には、晴れなかった場合にどのようなことをしたとしても、それが嘘をついたことになるわけではないと考えられる。
雨が降って行かなかったとしたら、それはそれで子どもも納得するであろうし、まして雨が降ったのに出かけたとしたら期待以上の良き父親ということになるだろう。いずれにしても父親が「嘘つき」と子どもから言われる状況にはならないので、この事情から3行目と4行目のA⊃B列はどちらにも真が与えられる。
さて以上が前件A、後件Bと、演繹言明「AならばB」(理論A⊃B)の真偽関係だが重要なのはここからである。
これまでは、事実A、事実Bと理論A⊃Bの真偽関係を確認するために、Aの真偽とBの真偽が確定しているときのA⊃Bの真偽がどのようであるかをみてきた。それによって、真理表に示されているA、B、A⊃B 間の真偽関係が納得のいくものであることが了解されたものと思う。これ以後は、この真理表を使って次の問題を考える。
それは、前件肯定式(A⊃Bが真、かつAが真)が導く結論Bは正しいか、ということである。つまり、これまではAとBが確定しているときのA⊃Bの状態をみてきたが、これ以後は、理論A⊃Bと前件Aの事態が確定しているとき、結論Bがどうなるのかに注目する。
再び父親の例で考えてみる。A⊃Bが真であるということは、父親が言った「明日晴れたら動物園に行く」という言葉に絶対に嘘はなく、その約束が果たされることは確実であるということである。そして、Aが真であるということは当日晴れたということである。そこで先の真理表からAが真で、かつA⊃Bが真である行を探すと1行目だけがそれに該当していることがわかる。
この真理表は、ありえる世界のすべてを表現しているものであったから、この場合、ありえる4通りの事態の内一つの事態だけが該当しているといえる。すなわち「明日晴れたら動物園に行く」という約束が真実で、しかも当日晴れたという場合には結論は一つしかなく、しかもそのときのBの値は真、すなわち「動物園に行く」という結論であるということである。
このようにして前件肯定式「AならばBであり、かつAである」が導く結論は常に真であることが明らかである。それは前件肯定式においては、事態が一意に定まるからであり、この場合、我々は彼らが動物園に行くかどうかを観察することなく論理だけから知ることができる。
補足だが、A⊃Bが真で、かつAが偽の場合、つまり当日雨だった場合には事態は一意に定まらず3行目と4行目の二つの事態が可能となる。この場合、Bは1、0の両値を示しているので、我々は、父親が子どもと出かけるかどうかは論理だけからは知ることができず、実際に彼らを観察してみなければわからないということになる。
また、A⊃Bが正しければAもBも正しいにきまっているというわけではない。A⊃Bが正しいということは、単に整合的な理屈が述べられたということにすぎず、その事態を真理表でみると、1行目、3行目、4行目が該当しており、その場合、前件Aと後件Bは真偽どちらでもありえることがわかる。つまり単に「筋の通った話」が真実とは限らないということである。