| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (6)
Easy Study 2-2 真理表
ここで真理表についてもう少し詳しく見ておこう。これまでの「前件肯定式推論」や、次節にみる「後件肯定式推論」では、真理表が何を行っているものかについての正確な理解を持つことが絶対に必要であるというわけではない。前節でのように常識を働かせながら表を眺めることができれば、それらの論理式の意味を十分に理解できる。
しかしEasy study 5で扱う「直観主義命題論理」という論理形態では、上のような常識に頼った見方がかえって理解を難しくするので、ここで論理学の基本となる概念をしっかりと押さえておき、後にもう一度この箇所に戻って確認できるようにしておこう。
理解しておきたいのは「真理表で何が定義されているか」ということと、「論理的真理」という概念、および「真理値分析」である。以下は引き続き、野矢茂樹『論理学』を参照しながら、これらの点を補足したものである。
先の「Ａ⊃Ｂの真理表」では結合子⊃の意味が定義されている。そこでは⊃の意味に合うように１（真）と０（偽）が配置されているというのではなく、逆であって、１、０をそう配置することによって⊃の意味を定めているのである。⊃は、その前件が真で後件が偽のときに、⊃で結ばれた言明全体を偽とする働きを持つことが定義されている。
⊃は「ならば」と読むが、「明日晴れたならば動物園に行く」と言う場合、「明日晴れた場合にだけ動物園に行く」が意味されていることもある。日常の言葉遣いとしてはこちらの方が普通かもしれない。「～ならば～する」という言明では、「～がそうでないならば～しない」が含意されていることが多いからである。
しかしこの意味での「明日晴れたならば動物園に行く」は、雨が降って動物園に出かけた場合には偽となる。ここでは「動物園に行くのは晴れたときだけ」と言っていたからである。しかし真理表Ａ⊃Ｂに定義された⊃では、前節に説明した通り、雨が降って動物園に行ったとしてもＡ⊃Ｂという父親の言明は嘘を言ったことにはならない。
つまり日常的に使われる接続詞「ならば」は、上にみてきた「Ａ⊃Ｂの真理表」の⊃とは働きが違っているのである。このような違いを明確に定義するのが真理表である。
論理学におけるＡ⊃Ｂは、その真理表にある通り１０１１が縦に並ぶものを言い「条件法」と呼ばれる。いま述べたもう一つの方の「ならば」は真理表に１００１が縦に並び、こちらは「同値」と呼ばれる。
繰り返すと条件法の⊃や同値（≡）の「ならば」が持つ意味が、真理表の１、０をそのように配置させているのではなく、１、０をそのように配置することで⊃や≡の意味を定めているのである。この１（真）、０（偽）は、前節に述べた対応説的な真理観としての真／偽を示すものだが、真理表の中では未定義であり定義する側の語として働いている。
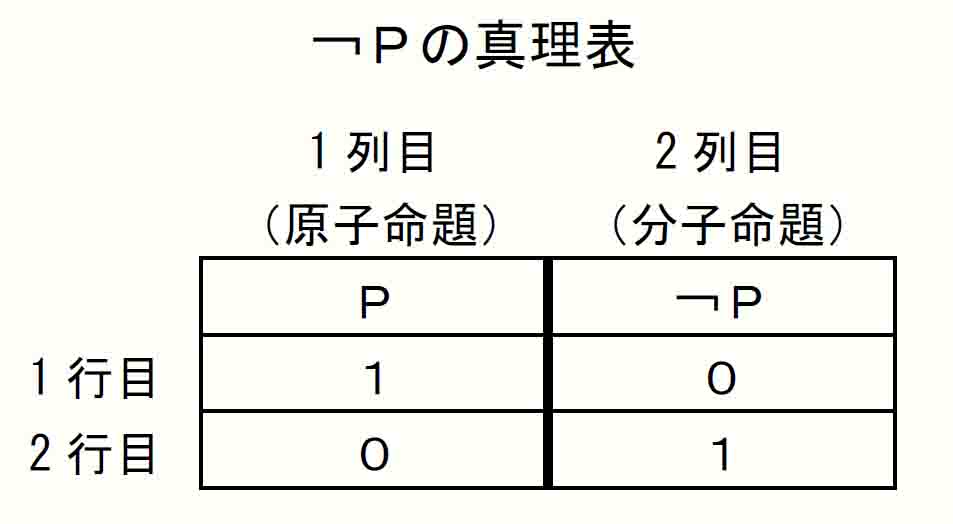
確認のためもう一つ、否定子￢「否」の真理表を掲げておく。以下のように￢Ｐの列の真理値を縦に０１と配置させることで￢が定義されている。命題Ｐに加えられた￢は、元の命題の真偽を逆転させる働きを持つということである。
次に「論理的真理」という概念を明確にしておこう。論理的真理とは元の命題の真偽に関わらず常に正しさが保たれる言明が持つ真理性のことをいう。
「明日は晴れまたは晴れではない」という言明は、明日の天候如何にかかわらず正しいので論理的真理を持つ言明である。「明日は晴れ」と主張して実際に晴れた場合、その主張は経験的真理を持つ言明である。経験的真理の言明は、事実との対応説的一致を待って初めて真理となるが、論理的真理の言明は経験に拠ることなく常に真である。
論理的真理である言明の真理表を作成すると、その言明の列には縦に１だけが並ぶ。これを確認しておこう。準備として、結合子∨「または」の定義を見ておく。
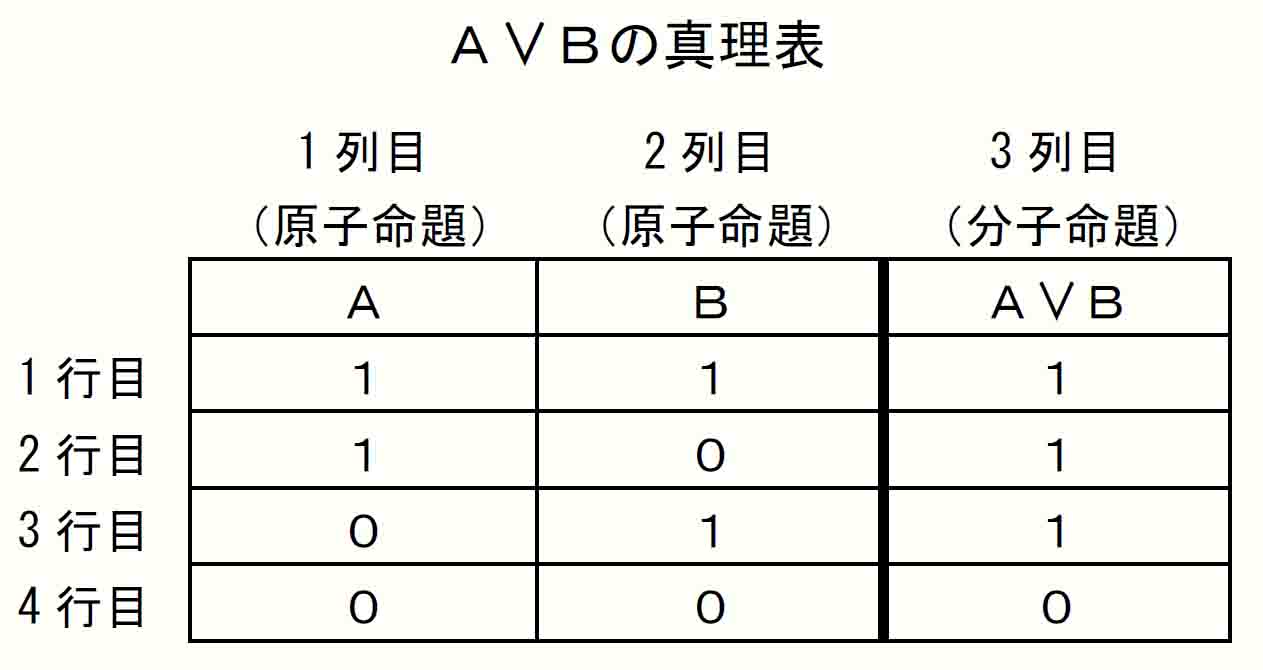
これも常識的な理解から表を読むことができるだろう。Ａ、Ｂのいずれか、あるいはその両者が真であるとき、「ＡまたはＢ」という言明は真となる。上の真理表では、この日常的な「または」の意味と合致する定義が∨に与えられている。
そこで「明日は晴れ」を命題Ｐとして、Ｐ∨￢Ｐすなわち「明日は晴れまたは晴れではない」を真理表で確認してみる。
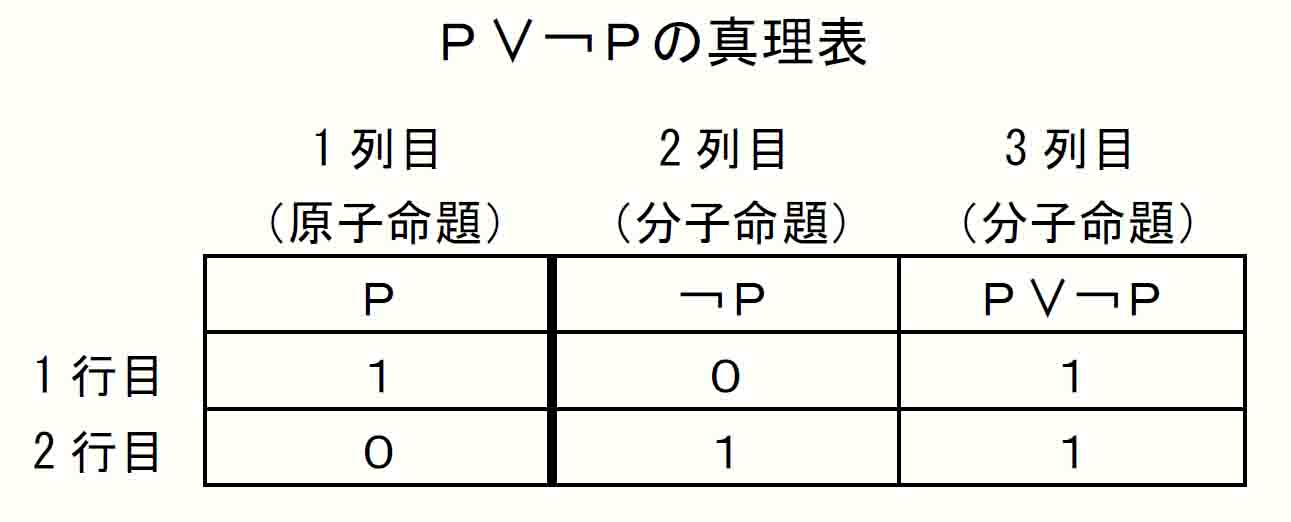
2行からなるＰ∨￢Ｐの真理表を「Ａ∨Ｂの真理表」に照らすと、その1行目は「Ａ∨Ｂの真理表」の2行目に相当し、2行目は「Ａ∨Ｂの真理表」の3行目に相当することがわかる。そこでＰ∨￢Ｐ列の1行目と2行目には、Ａ∨Ｂ列の2行目、3行目と同じく１、１が与えられる。
こうして「Ｐ∨￢Ｐ」は、元のＰの事態がどうであれ（１であれ０であれ）常に真実な言明となることがわかる。ある命題の肯定と否定が∨で結ばれたこのような言明は「排中律」と呼ばれる。
このように真理表の縦列がすべて１となる言明を「トートロジー」といい、真理表によって命題の真偽を扱える「古典命題論理」では、このトートロジーが「論理的真理」の指標である。
確認のためにトートロジー言明をもう一つみておこう。「排中律」と並ぶトートロジーのいま一つの代表は先にもみた「前件肯定式」である。
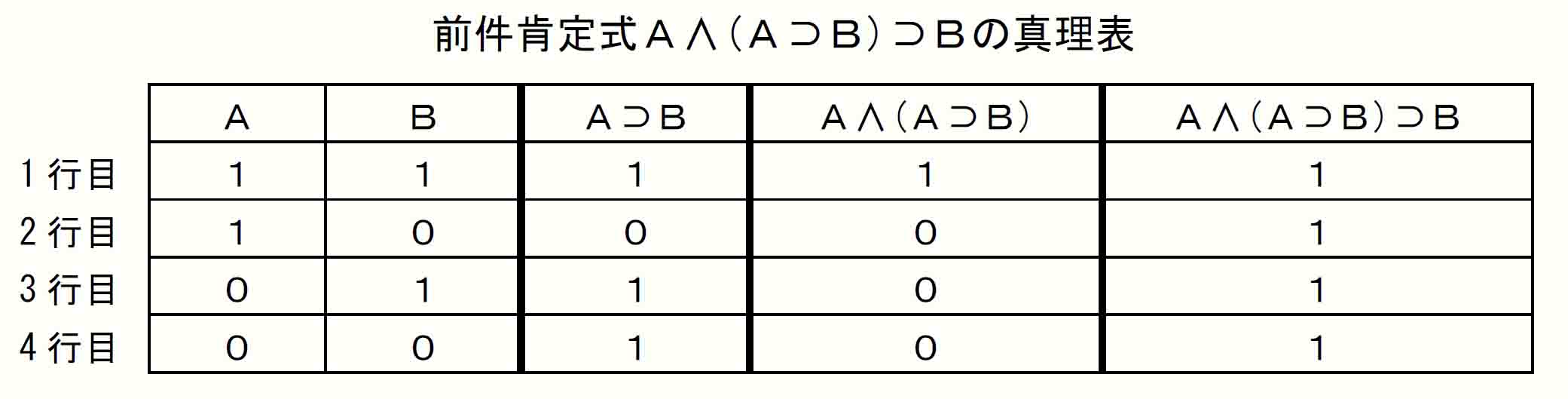
先にデカルトの『省察』に触れたところでは、前件肯定式の正しさを哲学的な真理論の観点から、前件を真理の対応説による保証、推論部を真理の整合説による保証に基づく正しさとしたが、論理学の観点からは、その推論部が前件肯定式すなわちトートロジーであることが「推論の正しさ」の保証となっている。これを以下で確認してみる。
推論を論理式で表すと△⊃○という形になるが、ここで「推論の正しさ」というのは「前提△が正しいときに結論○が必ず正しいものとして導かれること」をいう。
そこで、⊃の前件△が真の場合に、後件○が必ず真となる論理式とはどのようなものかを考えてみる。
まず、△⊃○がトートロジーである場合を考えてみると、この論理式では、△や○を構成する元の原子命題の値がどうであれ、真理表の△⊃○の列には全行に１が入る。それがトートロジーの定義である。上の「前件肯定式Ａ∧(Ａ⊃Ｂ)⊃Ｂの真理表」の列を入れ替えて、推論順の並びにした真理表は以下のようになる。
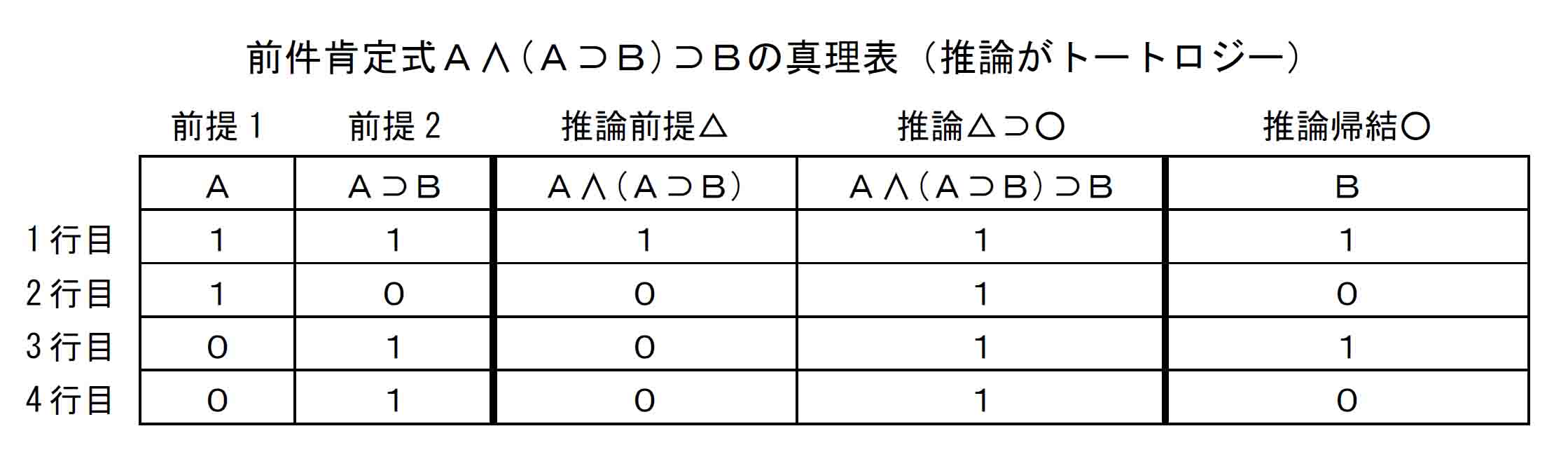
これと、前節で見たＡ⊃Ｂの真理表を比べてみる。こちらも推論における前提、推論、帰結の順に列を入れ替えたものを掲げる。2つの真理表の「推論前提△」の列同士と、「推論△⊃○」の列同士を比べてみよう。
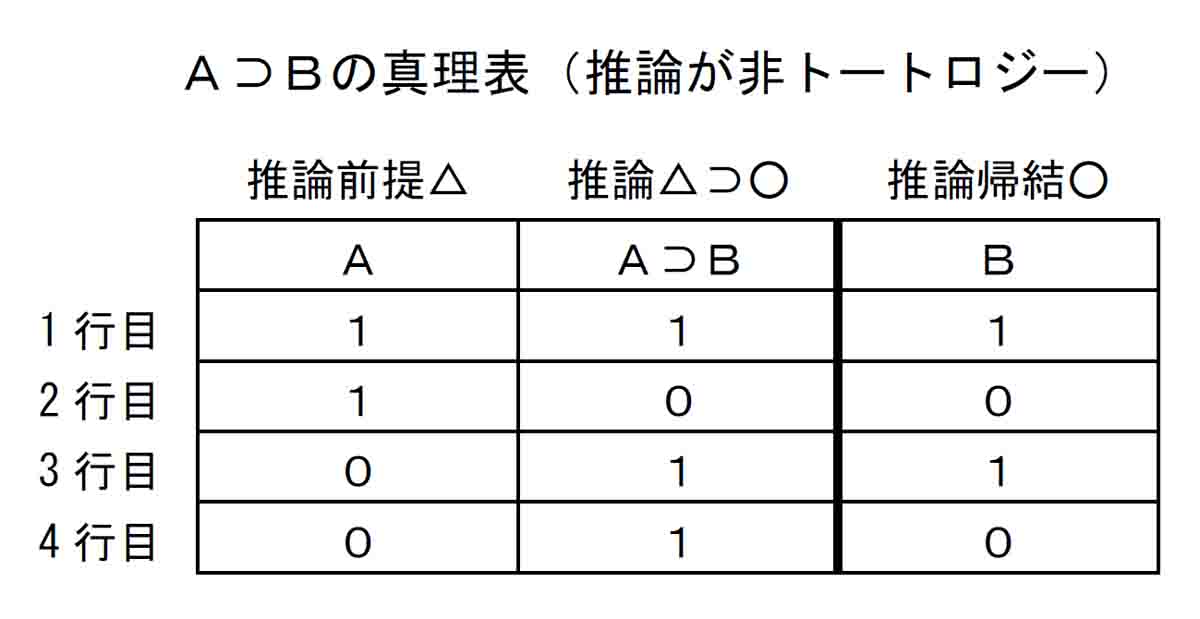
Ａ、Ｂを原子命題とするＡ⊃Ｂの真理表は、△⊃○の列（Ａ⊃Ｂ列）の全行に1が入るわけではない。しかし、Ａ⊃Ｂが真でＡが真の場合であれば事態は一意に定まり（1行目）、このときＢは真である。
いま△⊃○の形をした論理式がトートロジー、すなわち△⊃○列の真理値がすべて１となる論理式を考えているが、これと「推論の正しさ」の条件である「前件△が真であること」とを合わせると、この事態においては、Ａ⊃Ｂの真理表の1行目の事態が起きているとすることができる。
そこでこのＡ⊃Ｂの真理表の1行目の事態を、前件肯定式の真理表で見てみると1行目がそれに該当していることが分かる。そしてその際のＢの値は１である。△⊃○とＡ⊃Ｂの「⊃」の働きが同じであり、△⊃○とＡ⊃Ｂの真理値が同じであり、△とＡが同じ真理値であるとき、残る○とＢが同じ真理値を持つことは道理である。
このように、Ａ⊃Ｂの真理表は、論理式△⊃○がトートロジーで、前件△が真の場合、後件○は必ず真となることを教える。したがってトートロジーである論理式は、前提が正しいときに結論が必ず正しいものとして導かれる「正しい推論」となる論理式である。
では逆に、トートロジーではない論理式が「誤った推論」となることは確かなのだろうか。トートロジーが「正しい推論」を与える論理式であるとしても、そのことがトートロジーではない論理式を「誤った推論」とすることには必ずしもならないような気もする。このところを確認しておこう。
まず、用語について整理しておく。というのも「推論の正しさ」あるいは「正しい推論」という言い方には誤解の余地があり、「推論」も「正しさ」も紛らわしい言葉だからである。
推論を△⊃○の論理式として表したとき、△を「前提」または「推論前提」と呼び、○を「帰結」または「推論帰結」と呼ぶ。
△⊃○については、「⊃」の働きについて述べるときは「推論」と呼び、推論の形式として△⊃○全体を述べる場合は「推論の論理形」と呼ぶ。そして真理表の各行レベルでの△⊃○の推論を「個々の推論」と呼ぶ。
△⊃○の真理表は、原子命題の真偽の組み合わせを異にする複数の「個々の推論」の行から成るが、「推論の正しさ」や「正しい推論」における「推論」とは、それら「個々の推論」のことではなく、推論の論理形である△⊃○のことをいう。
例えば、前件肯定式が「正しい推論」すなわち「前提が正しいときに結論が必ず正しいものとして導かれる推論」であるというとき、それはＡ∧(Ａ⊃Ｂ)⊃Ｂのことであり、Ａ、Ｂに具体例を適用したときに正しい帰結となるこの真理表の1行目をいうのではない。「正しい推論」としていわれる「推論」とは真理表レベルのものであり、真理表の各行レベルの「個々の推論」のことではない。
さて、「個々の推論」には、前提△が正しい時に帰結○が正しくなるもの及び不正となるもの、そして、前提△が正しくない時に帰結○が正しくなるもの及び不正となるものの4種類がある。そこで「個々の推論」を以下の3種類にまとめる。
「個々の推論」のうち、
前提△が正しくないものを「前提が正しくない推論」と呼ぶ。このとき△⊃○はＡ⊃Ｂの真理表に従って1。
前提△が正しく、帰結○が正しいものを「適切な推論」と呼ぶ。△⊃○はＡ⊃Ｂの真理表に従って1。
前提△が正しく、帰結○が不正であるものを「不適切な推論」と呼ぶ。△⊃○はＡ⊃Ｂの真理表に従って0。
そこで、上の二つの真理表（トートロジーであるＡ∧(Ａ⊃Ｂ)⊃Ｂ、非トートロジーであるＡ⊃Ｂ）から以下の2点を確認する。
<1> △⊃○がトートロジーである前件肯定式の真理表の個々の推論には「前提が正しくない推論」（2,3,4行目）と、「適切な推論」（1行目）が含まれている。
<2> △⊃○がトートロジーではないＡ⊃Ｂの真理表の個々の推論には「前提が正しくない推論」（3,4行目）と、「適切な推論」（1行目）と、「不適切な推論」（2行目）が含まれている。
<1>は、推論の論理形がトートロジーである推論には「不適切な推論」が含まれないということであり、このことは、前提が正しい場合には常に正しい帰結が導かれることを意味している。「個々の推論」のうち、前提が正しいのは「適切な推論」と「不適切な推論」だけだからである。
<2>は、トートロジーではない推論では、推論の中に、前提が正しくても帰結が偽となる「不適切な推論」が含まれているということだが、この事態はＡ⊃Ｂに限ったことではなく、トートロジーではない推論には必ず「不適切な推論」が含まれることになる。
というのも、トートロジーではない推論の真理表では△⊃○列が0（偽）である行が必ず存在する。それが△⊃○がトートロジーではないことの定義である。すると⊃の定義により、その行の前提△は真でありながら、帰結○は偽である。したがってこの行は「不適切な推論」であり、それゆえトートロジーではない推論は、前提△が正しいときに常に正しい帰結○を導くという、真理表レベルでの「正しい推論」とはならないのである。
ここまで、真理表レベルの「正しい推論」と各行レベルの「適切な推論」を分けて述べてきたが、それはこれらの混同による理解の混乱を避けるためだが、ここで参照している野矢茂樹『論理学』にはない「適切な推論」という用語を新たに作成したことにはいま一つの理由がある。それはこの「適切な推論」が、前世紀のポストモダン哲学以降、再評価され重要な概念として認識されてきたという事情があるためである。
次節と次々節に述べる「実在論」と「解釈学」は、いずれも後件肯定式推論というトートロジーではない推論を基礎とする考え方であり、論理学的には「正しい推論」ではない。しかしそこに「適切な推論」（下記真理表の1行目）が含まれていることによって、この後件肯定式推論は哲学および科学において「重要な推論」となっているのである。（詳細は次節以降を参照。）
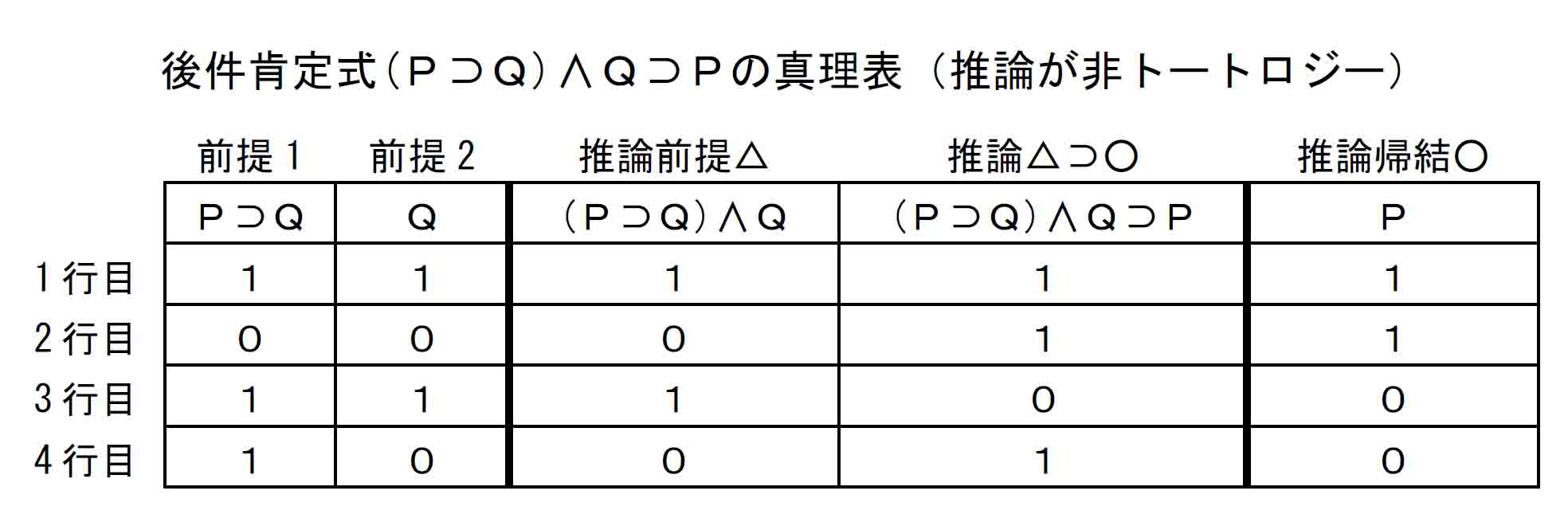
「正しい推論」に寄り道したが、真理表を多方面から検討したので真理表についての理解が深められたことと思う。改めて、トートロジーである論理式は真理表に１だけが縦に並ぶこと、そしてEasy study 4までで扱っている「古典命題論理」においては、トートロジーであるということが論理的真理であるということを押さえておこう。（後に見る「直観主義命題論理」ではトートロジーとは別の基準が論理的真理となる。
基本的な論理記号である￢、∨、∧、⊃、≡を定義する各真理表を使って、複合的な論理式の真理表を作成することを「真理値分析」という。先に、Ｐ∨￢Ｐの真理表をＡ∨Ｂと￢Ｐの真理表に基づいて作成したこと、前件肯定式、後件肯定式の真理表、および注[6]内で、前件否定式、「同値解釈による鯨の推論」の真理表を、￢と∧と⊃と≡の真理表に基づいて作成したことがこれにあたる。
以上、「真理表で何が定義されているか」、「論理的真理」、「真理値分析」について確認した。これらの概念は「古典命題論理」と「直観主義命題論理」を通じて機能する概念であるので、後の「直観主義命題論理」を扱う段では、これを足がかりにして理解を進めることにしよう。なお、次節以下「実在論」と「解釈学」は、いったん野矢茂樹『論理学』を離れての説明である。