| 第二部 信仰と理性論 | 星加弘文 |
Chapter 2 信仰と理性の多対多関係 (16)
Hard study 5-3-3 「否定証明のない命題は必ず証明される」という直観主義論理の奇妙さ
以上で、意味論と構文論間に認められる矛盾についての疑問は解けたが、しかし疑問はこれだけではなかった。Ⅱ(5)(ロ)が述べる「否定が証明されていない命題はやがて肯定が証明される」という、この内容そのものが難しさを感じさせる主張なのであった。どういう世界が考えられているのだろうか。
見てきたように、直観主義論理クリプキ意味論には3つの認識史がある。Ⅱ(5)(ロ)をHard study 5-2-4の「直観主義論理の¬Pの証明表」に照らしてみると、これが認識史11と認識史01の状況を述べたものであることがわかる。αで¬Pの不証明は認識史11と認識史01に認められ、それぞれのPは~βで⊩が得られている。
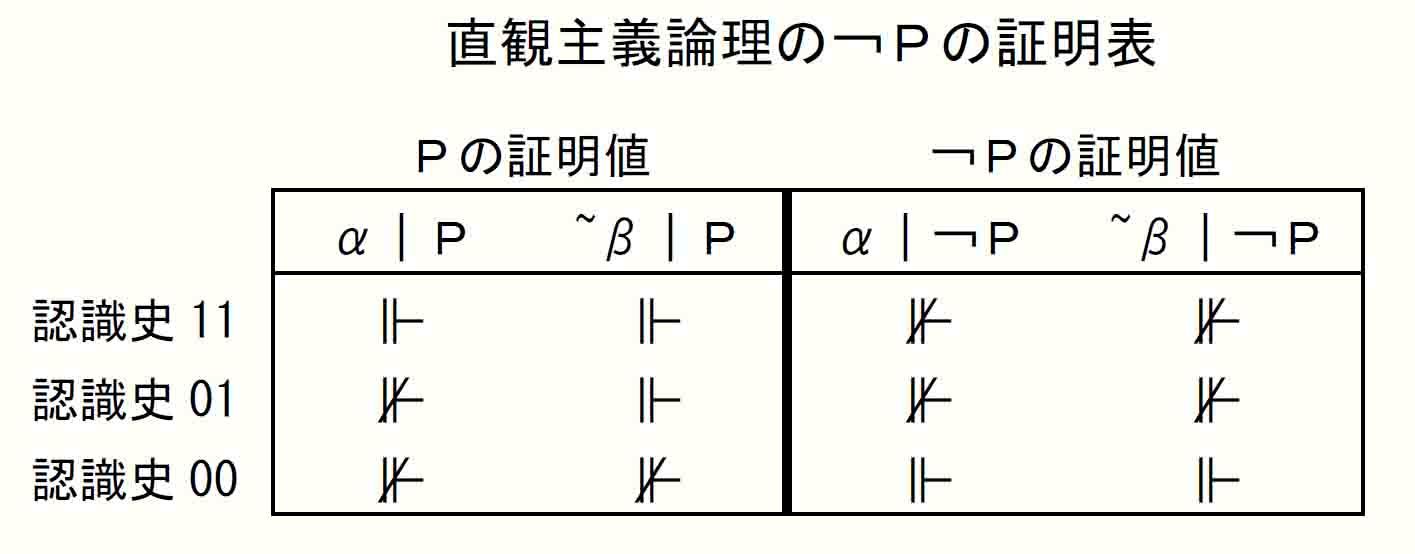
したがって、Ⅱ(5)(ロ)はすべての事象について「否定が証明されていない命題はやがて証明される」という認識史01の事態となることを言っているわけではない。認識史11は「否定が証明されていない命題はすでにその肯定が証明されている」という古典論理的な事態を言うものである。加えて、認識史00を見ればこちらも古典論理的な知識状態の表現である。
つまり、直観主義論理はすべての命題について「否定が証明されていないものはやがて証明される」ということを言っているわけではなく、認識史00のような「否定が証明されている命題はその肯定は最後まで証明されない」事態も当然ながら含んでいる。
しかし直観主義論理は、「否定が証明されていない命題が後に証明される」認識史01の知識状態が存在することを述べており、その場合、上の「¬Pの証明表」からは頭初期ではその命題の肯定も否定も証明されていない状況にあることが分かる。そのような、むしろ我々の実際においてはそれが現実的であるような知識状態にある命題について、認識史01は将来的にはそれが証明されるということを告げているのである。つまり、肯定も否定も証明されていない命題が将来に亘り不証明が続くという事態を直観主義論理は持たない。
したがって、やはり意味論規則(ロ)は不思議なことを述べている規則として理解しなければならない。
一方、Ⅱ(5)(ハ)は「後続期すべてで肯定が証明されないことが明らかになった命題は、頭初期で否定が証明されている」と述べる。ここでπの無限小数列の例をもう一度思い出してみる。
命題Aを「πの小数には0が100個続く列が存在する」とすると、(ハ)でいう「肯定が証明されない」とは、とりあえずは「0が100個続く列が現れない」ことである。(ハ)ではこの「0が100個続く列が現れない」ことが「後続期すべてで明らかになった」場合に命題Aの否定が証明されると言っている。
ところがπの小数列は無限であるため、命題列の現れないことが「後続期すべて」について明らかになる事態というのは永遠に訪れない。命題列が現れて肯定が証明されることは起こりえるが、命題列が現れないことが確定する事態は起こりえないのである。この結果、¬A「πの小数には0が100個続く列が存在しない」が明らかになる可能性は全くないことになり、したがってもちろん頭初期でそれが証明されているということはない。
これがⅡ(5)(ハ)が述べていることだが、このことは Easy Study 5-1 で、特にこの意味論を意識することなく得ていたπの小数列に関する理解に沿うものである。つまりπの小数列の例ではⅡ(5)(ハ)の言明は十分に理解できるといってよい。
そしてこれが理解できることの鍵となっているのは、πの少数列の無限という性質であることも明らかである。とすれば、(ハ)と同じく、(ロ)で言われている「後続期」もまた「無限の後続期」と解すれば、(ロ)は理解できる主張となるのだろうか。これを確認してみよう。
便宜のため「直観主義論理¬Pの証明表2」を再録する。
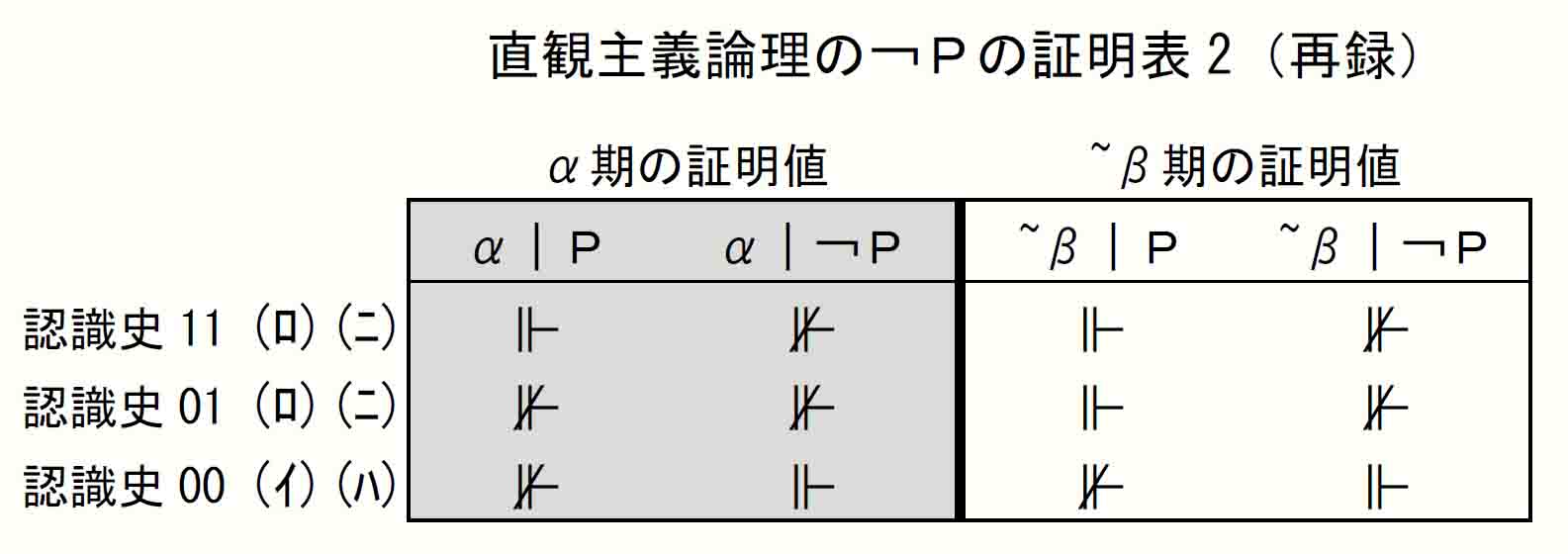
(以下、青=πの小数列の考察への言及、赤=「直観主義論理の¬Pの証明表2」についての言及)
確かに上表の認識史01からは、Ⅱ(5)(ロ)が述べていることを確認できる。認識史01ではα期でPも¬Pも不証明のとき、~β期ではPが証明され、¬Pは不証明のままである。これはπの無限小数列に対する命題Aの現時点の状況をそのまま示すものでもある。現在、命題Aの肯定も否定も不証明だとすると、しかし将来的にあるのはAの証明のみであり、¬Aが証明されることはないことはすでに見てきた通りである。
つまりπの無限小数列の世界では、不証明の命題Aは将来的には肯定証明の可能性しかないのだが、(ロ)はこのことをもって「後続期のどこかで肯定が証明される」といっているのだろうか。しかし肯定の可能性しかないとしても、それを肯定の必然とみてよいのかはなお判然としない。確かに古典述語論理では、選言が無限に続く命題をその命題の存在と同義とするが、肯定の可能性だけが無限に続くとき、それは肯定証明が存在することと同義なのだろうか。
しかし「直観主義論理¬Pの証明表2」認識史01は明瞭にそのことを示している。これによればPも¬Pも未証明のとき、将来においてPは必ず証明されるのである。ここではPは証明されることだけを待つ身分の命題である。三値論理とは異なり、直観主義論理の真偽不明は真の可能性を持った不明である。
そして認識史が無限に続けば、その肯定も否定も不明であるようなあらゆる命題は必ずその肯定が証明されることになるというのが直観主義論理認識史01の世界観であるようにみえる。
あるいは、πの小数列の例は、そのような世界を我々に垣間見させるものであるのかもしれない。というのも、πの小数列には規則性がないということなので、仮にこれを0~9までの数字がランダムに出現する文字列と解することが許されるなら、0が100個続いて出現することは十分にありえることだからである。
6面のサイコロ1個を振って2度続けて1の目が出るためには6^2+1=37回サイコロを振ればよい。以下では大きな数を見るのでここでの+1相当分は無視するとして、同様に、10面のサイコロを振って100回連続して0を出現させるには10^100回振れば可能である。(なお、正十面体というのは存在しないが、同形のたこ形を面とする10面サイコロは出回っている。あるいは0~9を2箇所ずつに書いた正二十面体のサイコロを使うとする。)
2019年時点でπの小数列は31兆桁まで計算されたということだが、それは10面サイコロを3.1×10^13回振ったことに相当する。したがって現時点ではサイコロを投げる回数がまだまだ足りないのだが、やがて10^100回、10^200回と振っていけば、ほぼ必ず0が100回連続して出現する機会を得るはずである。
すると振る回数が無限であれば、どんな事態もすべて出現するということも想像できるだろう。このように考えると、肯定の可能性しかなくしかもその証明機会が無限であるような世界では、未証明の命題は必ず証明されるとしてよいのかもしれない。
さて以上のことから、対象が無限である場合、少なくともπの小数列の例で、我々は(ロ)の言明を理解できるとしてよいだろう。
次に、Ⅱ(5)(ロ)の「後続期」を有限と考えた場合に、(ロ)の主張を理解できるかを考えてみたい。対象が有限であるということは、我々が住む世界の中に具体例があるということでもあるので、それを考えてみたい。もしここに適切な例があれば、扱う事象の無限であることが直観主義論理が適用されるための要件であるというのでは必ずしもない、ということにもなる。
先に引用した「勇気」の例でもよいが、より曖昧さが少ないと思われる Easy study 5-1 の冒頭に挙げていた「事件」の例での「罪の立証」を取り上げてみる。
「自由心証主義」を採用する日本の司法では、犯罪が行われたことの直接的な証明が行われなくても裁判官の心証によって有罪が言い渡されることがある。しかし通常は犯罪の立証がなければ心証が成立せず、無罪が言い渡される。
司法の世界では罪の存在は有罪立証と一体であって、証明されることで初めて法的な罪が存在し、証明されなければ罪は存在しない。時効のある犯罪では、定められた有限の期間内に犯罪を立証できなければ罪がないことになる。
「勇気」について野矢氏は「観察するチャンスがあるかどうかにその存在が関係してしまうような」と述べていたが、司法における「有罪」は文字通りそのようなものといえるだろう。有罪は「証明できるかどうかにその存在が関係する」ものである。
このことからは、扱う対象が無限であることが直観主義論理を適用するための条件なのではないことが窺える。無限にもそれを認めうるような何らかの性質を持つ対象が、この論理の対象物なのである。しかしその性質とは何だろうか。(これについてのまとめは Hard study 5-4-4 の終わりを参照)
ここで煩を厭わず「直観主義論理¬Pの証明表2」をもう一度眺めながら、さらに直観主義論理の性質について考えてみよう。

先に、「直観主義論理の¬Pの証明表2」を挙げた Hard study 5-3-1 ではα期に注目したが、ここでは~β期に注目してみる。
~β期では、いずれの認識史においても、必ずPか¬Pかのいずれかが証明されており、また、その場合において当然のことだが、そのときそれぞれ逆側の命題は不証明となっている。
改めて見ると意外な感じもするが、つまり直観主義論理においても、最終的には古典論理と同様に、P∨¬Pは排中律として成立しているということである。ここにはα期で想定されていた肯定も否定も証明されない最終事態というものはないことが示されている。このことは、Hard study 5-2-4「直観主義論理のP∨¬Pの証明表」において、すべての認識史の~β期で⊩が成立していることにすでに表れていたことでもある。
初めは肯定も否定も証明できないような命題であっても最終的には証明に委ねられていく世界、どんな命題であれ最終的には古典論理と同じく、その肯定か否定が明らかになる世界、そのような世界が考えられているといえる。
しかし現実の世界では、有罪が証明されなくても犯罪は行われていたということや、有罪になったとしても実は無実であったということがいくらもある。実際の「罪の立証」の場面では、証明されることと犯罪の有無は別であって、司法の場での証明はあくまでも事実に迫ろうとするものであるにすぎない。
証明の有無に関わらず、事実は変えようのないものとして証明や論理からは独立して存在しているというのが、我々の常識において理解する世界と論理の関係である。我々にとって真理とは事実のことにほかならない。そして事実は神のみが知っているとすれば、この真理たる事実について、我々がそれを知りえるか否かに関わらずその真偽を扱おうとする古典論理が、ときに「神の論理学」と呼ばれることがあることもまた理解できることである。
しかし直観主義論理が示す世界はそのようなものとは明らかに違っている。それは観念論哲学が知識の源泉として認めてきたところの我々の感覚、観察、証言、証明といったものたちをすべてとする世界といえる。
そこでの存在とは我々にとって明らかにされているもののことであって、事実は証明と一体であり、事実とは「証明されたこと」や「見たもの」のことに他ならない。そのような事象として知られているのは、これまでのところ上に挙げてきたものたちだけのようにも思われる。
すなわち、まず論理学や数学の世界。数学ではある概念が矛盾なく構成できる場合に、その概念を「存在する」とする。裁判所の中の世界も、証明・不証明が支配する世界といえる。そこでは事実への予断は避けられ、証拠や証言によってのみ、司法版の「事実」が積み上げられていくのである。
その結果、否定証明が最後まで行われなかった場合、「直観主義論理¬Pの証明表2」が示すところにより、必ず有罪/無罪の最終決着がつけられることになる。司法の世界のβ期は有限だからである。そしてこのとき、最初に肯定命題として立てられていたものが証明されたとされる。現実の司法は、そのように決着をつけることで体制を維持しており、直観主義論理が支配する世界なのである。
奇妙に思われた直観主義論理意味論Ⅱ(5)(ロ)であったが、とりあえずは理解できるものになったとしてよいだろう。直観主義論理は、πの小数列や犯罪事象が含んでいる未知や不明といったものを相手にした論理学である。ただしこの「不明」や「未知」を、単に「真」「偽」に加わる第3の真理値とするというのではなく、それらの不明や未知をやがて知られていくことが可能であるものとみる論理学である。
なお、「真」「偽」に第3の真理値を加える論理学として三値論理があるが、直観主義論理と三値論理の違いについては Hard study 5-4-3 に改めて述べる。